 |
Виды понятий. Отношения между понятиями.
|
|
|
|
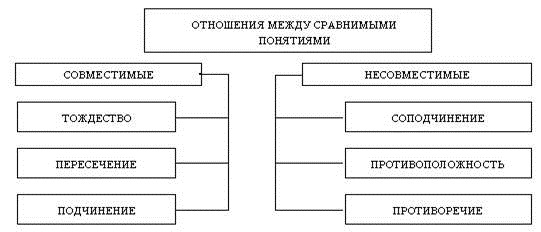
В зависимости от содержания и объема все понятия делятся на конкретные виды. Для наглядности представим их в виде схемы, а затем последовательно рассмотрим каждый вид более подробно. Единичными называются понятия, в которых мыслится один предмет (например, "великий русский писатель Александр Николаевич Островский", "Организация Объединенных Наций", "столица России" и другие).
Общим называется понятие, в котором мыслится множество предметов (например, "столица", "государство", "правовед", "экономист" и другие). Общие понятия могут быть регистрирующими и нерегистрирующими.
Регистрирующими называются понятия, в которых множество мыслимых в них предметов подается учету, регистрации (например, "участник Великой Отечественной войны", "народный депутат России" и другие). Нерегистрирующим называется общее понятие, относящееся к неопределенному числу предметов (например, "человек", "философ", "ученый" и другие). Нерегистрирующие понятия имеют бесконечный объем.

Нулевыми (пустыми) называются понятия, объемы которых представляют собой классы реально не существующих предметов и существование которых в принципе невозможно: "вечный двигатель", "русалка", "леший" и др.). От нулевых следует отличать понятия, отражающие предметы, которые реально не существуют в настоящее время, но существовали в прошлом или существование которых возможно в будущем: "древнегреческий философ", "термоядерная электростанция". Такие понятия не являются нулевыми.
Конкретные - это понятия, в которых мыслится предмет или совокупность предметов как нечто самостоятельно существующее: "академия", "студент", "романс", "дом", "поэма А. Блока "Двенадцать" и др.
|
|
|
Абстрактные - это понятия, в которых мыслится не сам предмет, а какой-либо из признаков предмета, взятый отдельно от самого предмета: "смелость", "добросовестность", "храбрость", "синева", "тождество" и др.
Относительные - это такие понятия, в которых мыслятся предметы, существование одного из которых предполагает существование другого: " родители "-" дети "," учитель "- "ученик "," начальник "-" подчиненный "," истец "-" ответчик " и др.
Безотносительные - это такие понятия, в которых мыслятся предметы, существующие самостоятельно, вне зависимости от другого предмета: "фермер", "правило", "деревня", "человек" и др.
Положительные - это понятия, содержание которых составляют свойства, присущие предмету: "принципиальность", "благородный поступок", "живущий по средствам", "успевающий студент" и др.
Отрицательными называются понятия, в содержании которых указывается на отсутствие у предмета определенных свойств (например, "некрасивый поступок", "некрашеный дом", "некошеный луг" и др.). В русском языке отрицательные понятия выражаются обычно словами с отрицательными приставками "не" или "без" ("бес "): "неграмотный", "неверующий", "беззаконие", "беспорядок" и др. В словах иностранного происхождения - чаще всего словами с отрицательной приставкой "а": "агностицизм", "аморальный" и др.
Собирательными называются понятия, в которых группа однородных предметов мыслится как единое целое: "лес", "созвездие", "роща", "студенческий строительный отряд" и др. Содержание собирательного понятия нельзя отнести к каждому отдельному элементу, входящему в объем этого понятия.
|
|
|
Несобирательные - это такие понятия, содержание которых можно отнести к каждому предмету данного класса, который охватывается понятием: "дерево", "звезда", "студент" и др.
Определить, к какому из указанных видов относится конкретное понятие, означает дать ему логическую характеристику. Например, понятие "невнимательность" - общее, несобирательное, абстрактное, отрицательное, безотносительное. Логическая характеристика понятий помогает уточнить их содержание и объем, вырабатывает навыки более точного употребления понятий в процессе рассуждения.
6 отношения между понятиями
Отношения между понятиями принято иллюстрировать с помощью круговых схем (кругов Эйлера),где каждый круг обозначает объем понятия, а каждая точка - предмет, входящий в его объем. Круговые схемы позволяют наглядно представить отношения между различными понятиями, лучше понять и усвоить эти отношения.

В отношениях тождества находятся понятия, которые различаются по своему содержанию, но объемы которых совпадают. В таких понятиях мыслится один предмет или класс однородных предметов. Однако содержание таких понятий различно, так как каждое из них отражает только определенную сторону (признак) данного предмета или класса однородных предметов. Например, "автор рассказа "Человек в футляре" и "автор рассказа "Каштанка"
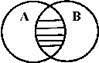
В отношении пересечения находятся понятия, у которых объемы частично совпадают. Содержание этих понятий различно. Например, пересекающимися понятиями являются "студент" и "филателист" (А и В): не все студенты являются филателистами, и не все филателисты - студенты. В совместившейся (заштрихованной) части кругов мыслятся те студенты, которые являются филателистами.
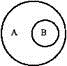
В отношении подчинения находятся понятия, объем одного из которых полностью входит в объем другого, составляя его часть. В таком отношении, например, находятся понятия "герой" (А) и "театральный герой" (В). Объем первого понятия шире объема второго понятия: кроме театрального героя существуют и другие виды: герой литературный, художественный, телеэкрана, кинематографический и другие. Понятие "театральный герой" полностью входит в объем понятия "герой".
|
|
|
При иллюстрации отношений между несовместимыми понятиями возникает потребность во введении более широкого по объему понятия, которое включало бы объемы несовместимых понятий.

В отношении соподчинения находятся два или более неперекрещивающихся понятий, принадлежащих общему родовому понятию. Соподчиненные понятия (В и С)- это виды одного рода (А), у них общий родовой признак, но видовые признаки различны. Например, "должностное преступление" (А), "взятка" (В), "растрата" (С).

В отношении противоположности (контрарности) находятся понятия, которые являются видами одного и того же рода, и притом одно из них содержит какие-то признаки, а другое эти признаки не только отрицает, но и заменяет их другими, исключающими (т.е. противоположными признаками). Например, "демократическое государство" и "тоталитарное государство " (А и В), "свой" и "чужой", "храбрость" и "трусость" и т.д. Слова, выражающие противоположные понятия, являются антонимами. Объемы противоположных понятий составляют в своей сумме лишь часть объема общего для них родового понятия.

В отношении противоречия находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками. Например, "знающий философию" и "незнающий философию", "друг" и "недруг" и т.д. Объемы двух противоречащих понятий составляют весь объем рода, видами которого они являются. Таким образом, уяснение логической структуры понятия, раскрытие их видов и отношений между сравнимыми понятиями дает возможность перейти к рассмотрению логических действий, или операций, над понятиями.
7 Обобщение и ограничение понятий.
Из множества других логических операций с содержанием и объемом понятий, рассматриваемых современной логикой, выделим две, весьма распространенные и важные, тесно связанные между собой. Это обобщение и ограничение понятий. В них непосредственно проявляется действие закона обратного отношения между содержанием и объемом понятия.
|
|
|
Обобщить понятие – значит перейти от понятия с меньшим обьемом, но с большим содержанием к понятию с большим обьемом, но с меньшим содержанием. Например, обобщая понятие «Министерство юстиции РФ», мы переходим к понятию «министерство юстиции». Объем нового (общего) понятия шире исходного (единичного) понятия; первое относится ко второму как индивид к виду. Вместе с тем содержание понятия, образованного в результате операции обобщения, уменьшилось, так как мы исключили его индивидуальные признаки.
Продолжая операцию обобщения, можно последовательно образовывать понятия «министерство», «орган государственного управления». Каждое последующее понятие, является родом по отношению к предыдушему.
Из приведенного примера видно, что для образования какого-либо нового понятия путем обобщения нужно уменьшить содержание исходного понятия, т. е. исключить видовые (или индивидуальные) признаки.
Обобщение понятия не может быть беспредельным. Наиболее общими являются понятия с предельно широким объемом – категории, например «материя», «сознание», «движение», «свойство», «отношение» и т.п. Категории не имеют родового понятия, обобщить их нельзя.
Ограничение понятий представляет собой операцию, противоположную операции обобщения. Ограничить понятия – значит перейти от понятия с большим обьемом, но с меньшим содержанием к понятию с меньшим обьемом, но с большим содержанием. Иначе говоря, чтобы ограничить понятие, нужно перейти от рода к виду: увеличить его содержание путем прибавления видовых признаков. Например, ограничивая понятие «юрист», мы переходим к понятию «следователь», которое в свою очередь можем ограничить, образовав понятие «следователь прокуратуры». Пределом ограничения понятия является единичное понятие (например, «следователь прокуратуры Иванов»).
Таким образом, изменяя объем исходного понятия, мы изменяем и его содержание, осуществляя тем самым переход к новому понятию – с большим объемом.
Значение логических операций обобщения и ограничения состоит в том, что они служат средством закрепления полученных знаний, как общих, так и частных, и одним из способов достижения определенности нашего мышления. Например, в судебной практике важно не только определить, является ли то или иное деяние преступлением вообще, но и установить его характер и степень общественной опасности, решить, относится ли оно к тяжким, менее тяжким или особо тяжким, и, наконец, дать его точную квалификацию: кража, грабёж и т.д. Это последовательная цепь ограничений. Наоборот, ложные ограничения – плеоназмы способны исказить мысль, вызвать кривотолки. Если я скажу: «памятный сувенир», то слушающие меня могут подумать, что есть еще непамятные сувениры. Все это особенно важно учитывать в юридической практике. Нельзя, например, говорить: «законное право». Иначе придется признать, что есть «незаконное право».
|
|
|
Операции обобщения и ограничения связаны с важнейшими для логики понятиями рода и вида.
Понятие А является родом по отношению к понятию В, если А может быть получено в результате обобщения В.
Понятие В является видом понятия А, если В может быть получено в результате ограничения А.
Нетрудно заметить, что для данного понятия В можно найти много родовых понятий. В дальнейшем нам понадобится выделить родовое понятие, самое близкое по объему к данному понятию.
Понятие А назовем ближайшим родом для понятия В, если не существует такого понятия С, которое является одновременно обобщением В и ограничением А.
Ясность и определенность мышления требует четкого различения, с одной стороны, отношения рода и вида, а с другой стороны, отношения целого и его части. Несмотря на вроде бы очевидность этого различения, эти отношения часто путают на практике, что приводит к недоразумениям при представлении объемов понятий, выполнении операций обобщения и ограничения, а также совершении некоторых типов умозаключений.
Часть предмета — это составляющая целого предмета, которая не обладает всеми признаками целого предмета.
Пример. Нога — часть человека, потому что она является его составляющей и не обладает всеми признаками, которыми обладает человек, например, «быть разумным существом».
Пример. Человек — часть коллектива, поскольку он является одной из составляющих коллектива, но не обладает всеми признаками, которые присущи коллективу, например, «быть группой людей».
В противоположность части предмета вид является частью не предмета, а объема более общего понятия.
Пример. Объем понятия «трудовой коллектив» есть часть объема понятия «коллектив», а следовательно, его вид.
Пример. Объем понятия «студент» есть часть объема понятия «человек», а следовательно, студент представляет собой вид человека.
Часть предмета можно также назвать физической частью целого предмета, а вид — логической частью более общего понятия.
8 деление понятий. виды деления
Логические операции предполагают уяснение отношений между понятиями не только по содержанию, но и по объему. Логическая операция, раскрывающая объем понятия, называется делением. Ее сущность заключается в расчленении известного класса предметов, охваченных данным понятием, на более мелкие классы.
Деление это такая логическая операция, в которой общее и отличительное, как две стороны каждой вещи, находят свое раздельное проявление - в подчинении видовых понятий общему роду и в соподчинении их между собой.
От логического деления понятий следует отличать расчленение предмета на отдельные части. Например, цельное представление самолета можно расчленить на фюзеляж, двигатель и крылья, а в результате логического деления понятия "самолет" получим его виды - гражданские и военные самолеты. Причем эти виды самолетов далее можно делить по их назначению, техническим характеристикам и т.д. Приведем другой пример. Так, дерево можно расчленить на ствол, ветки, корни и т.д. Однако это не есть операция деления на классы. В действительности же деление понятия "дерево" образует новые подклассы: хвойные и лиственные деревья.
Необходимо иметь в виду, что процесс логического деления понятий опирается на конкретные категории. Так, тот объем понятия, который подлежит делению, называется делимым понятием, а полученные видовые понятия носят названия членов деления. Существенный признак, по которому производится деление объема родового понятия на виды, называется основанием деления. Так, понятие "преступление" (делимое понятие) делится на такие понятия, как "умышленное преступление" и "неосторожное преступление". Они и составляют члены деления. А основанием в рассмотренном примере выступает такой существенный признак, как вина.
В логике выделяют ряд видов деления понятий:
дихотомия (т.е. деление на две части)
трихотомия (т.е. деление на три части)
политомия (т.е. многочисленное деление)
Частным случаем деления понятия по видоизменению признака является классификация. Это распределение предметов по группам (классам), где каждый класс имеет свое постоянное, определенное место. От обычного деления она отличается относительно устойчивым характером. Классификация сохраняется весьма длительное время, если она имеет научный характер. Например, в зоологии и ботанике члены деления животного и растительного мира закреплены на постоянные места в виды системы: тип - класс - отряд - семейство - род - вид.
Построенная на научной основе классификация имеет большое значение, служит важным средством обнаружения закономерностей в определенной области естественных и социальных явлений. Обоснованная классификация может сыграть важную роль в развитии наших знаний, помочь предвидеть зарождение новых научных направлений.
В процессе деления понятия необходимо соблюдать ряд правил, которые обеспечивают четкость и полноту деления.
Правило первое. Деление должно быть соразмерным. Это означает, что общий объем членов деления должен равняться объему делимого родового понятия, т.е. В+С=А. Например, в утверждении "звуки делятся на согласные и гласные" это правило учтено. Данное правило гарантирует от двух ошибок: а) неполного (с остатком) деления. Так, деление понятия "право" на государственное, административное, гражданское, уголовное будет неполным, с остатком; б) обширного (с избытком) деления. Например, утверждение "По значению имена существительные делятся на собственные, нарицательные и одушевленные" будет широким, с избытком. В этом предложении понятие "одушевленные" явно лишнее.
Правило второе. Деление должно производиться по одному основанию. Хотя объем одного и того же понятия можно разделить по-разному в зависимости от избранного основания, однако при однократном делении нельзя наряду с видами, соответствующими основанию деления, называть виды, ему не соответствующие. Ошибка, возникающая при нарушении этого правила, носит название "подмена основания" Ошибочно, например, любимое обращение деда Щукаря из романа "Поднятая целина" М. Шолохова к односельчанам: "Уважаемые граждане и старушки!" Здесь смешаны два основания - обращение к людям, являющимся гражданами страны, и обращение к женщинам пожилого возраста.
Правило третье. Деление должно быть последовательным. Это означает, что делимое понятие должно представлять ближайший род для членов деления, а члены деления должны быть непосредственными видами делимого понятия. Нельзя переходить к подвидам, минуя непосредственно видовые понятия. Нарушение этого правила ведет к логической ошибке "скачок в делении". Такую ошибку совершают, когда говорят: "Средства массовой информации делятся на государственные, коммерческие, местные, независимые и военные". Это неверно, так как средства массовой информации делятся на государственные и коммерческие, а те, в свою очередь, подразделяются на ряд подвидов.
Правило четвертое. Члены деления должны взаимно исключать друг друга. Согласно этому правилу, члены деления должны быть соподчиненными понятиями, их объемы не должны перекрещиваться. Нарушение этого правила связано с потерей основания деления. Например, при осуществлении классификации войн говорят: "Войны бывают справедливые, несправедливые, захватнические". Здесь допущена логическая ошибка. Захватнические войны относятся к числу несправедливых войн, и поэтому члены деления "несправедливые войны" и "захватнические войны" не исключают друг друга.
9 определение понятий. виды определения
Определение понятия (или дефиниция) есть логическая операция, которая раскрывает содержание понятия или устанавливает значение термина.
С помощью определения понятий мы можем раскрывать содержание понятия и тем самым отличать мыслимые в нем предметы от других предметов. Так, например, давая определение понятия “трапеция”, мы отличаем его от других четырехугольников - ромба, квадрата, прямоугольника или параллелограмма: “Трапеция - четырехугольник, у которого две стороны параллельны, а две другие - не параллельны” (1). Приведем еще несколько примеров определений понятий, взятых из школьных учебников: “Вещества, растворы которых проводят электрический ток, называются электролитами” (2); “Флорой называют видовой состав растений, произрастающих на той или иной территории” (3); “Естественный отбор - процесс выживания наиболее приспособленных особей, который ведет к преимущественному повышению или понижению численности одних особей в популяции по сравнению с другими” (4); “Алгоритм есть конечная последовательность общепонятных предписаний, формальное (не требующее проявления человеческой изобретательности) исполнение которых позволяет получить за конечное время решение некоторой задачи!” (5).
|
|
|


