Правила явного определения. Ошибки, возможные в определении

1. Определение должно быть соразмерным, т.е. объем определяющего понятия должен быть равен объему определяемого понятия.

Это правило часто нарушается, в результате чего возникают логические ошибки в определении. Типы этих логических ошибок:

а) широкое определение, когда определяющее понятие по объему шире, чем определяемое понятие. Такая ошибка содержится в следующих определениях: “Гравитация - это взаимодействие двух материальных тел”; “Лампа - источник света”. Понятие “окружность” неправильно определяется так: “Это фигура, которая описывается движущимся концом отрезка, когда другой его конец закреплен, или фигура, которая образована движущимся концом циркуля”. С помощью этого определения нельзя отличить понятие “окружность” от понятия “дуга”, так как не указано, что окружность - это кривая замкнутая линия;

б) узкое определение, когда определяющее понятие по объему уже, чем определяемое понятие. Например, “совесть - это осознание человеком ответственности перед самим собой за свои действия и поступки” (а перед обществом?);

в) Определение в одном отношении широкое, в другом - узкое. Например, “бочка - сосуд для хранения жидкостей”. С одной стороны, это широкое определение, так как сосудом для хранения жидкостей может быть и чайниц, и ведро, и т.д.; с другой стороны, это узкое определение, так как бочка пригодна для хранения и твердых тел, а не только жидкостей.

2. Определение не должно содержать круга. Круг возникает тогда, когда определяемое понятие и определяющее понятие определяются одно через другое.

В определении “вращение есть движение вокруг своей оси” будет допущен круг, если до этого понятие “ось” было определено через понятие “вращение” («ось - это прямая, вокруг которой происходит вращение”).

Круг возникает и тогда, когда определяемое понятие характеризуется через него же, лишь выраженное иными словами, или когда определяемое понятие включается в определяющее понятие в качестве его части. Такие определения носят название тавтологий.

Не могут считаться определениями из-за их тавтологичности следующие фразы: “Детектор - прибор, осуществляющий детектирование”, “Парамагнетик - вещество, обнаруживающее парамагнетизм”, “Сверхпроводник - вещество, обнаруживающее явление сверхпроводимости”, “Ферромагнетик - вещество, обнаруживающее ферромагнетизм”, “Фильтрование - процесс разделения с помощью фильтра”.

Логически некорректным является употребление таких, например, тавтологий, как “масляное масло”, “трудоемкий труд”, “порученное поручение”, “прогрессирующий прогресс”, “ заданная задача”, “изобрету изобретение”, “поиграем в игру”, “памятный сувенир”, “подытожим итоги” и др.

3. Определение должно быть четким, ясным. Это правило означает, что смысл и объем понятий, входящих в определение, должен быть ясным и определенным. Определения понятий должны быть свободными от двусмысленности; не допускается подмена их метафорами, сравнениями и т.д.

Не будут корректными определениями следующие суждения: “Краткость - сестра таланта” (А.П. Чехов); “Повторение - мать учения”; “Всякое стихотворение - покрывало, растянутое на остриях нескольких слов” (А. Блок); “Гармония есть согласие мировых сил, порядок мировой жизни” (Он же); “Грация - это красота отдельного предмета, а гармония - красота пространства, понятого как мир бесконечно сложный в замкнутый” (В. Фаворский); “Родительская любовь - любовь самая бескорыстная” (Рюноскэ Акутагава).

 

10 логические приемы образования понятий

Для образования понятия необходимо выделить существенные признаки предмета, применив с этой целью ряд мыслительных (логических) приемов: сравнение, анализ, синтез, абстрагирование, обобщение.

 

Сравнением является мысленное установление сходства или различия предметов по существенным признакам.

 

Анализом называется мыслительное расчленение предметов нм их составные части, выделение в них признаков.

 

Синтез – это мысленное соединение в единое целое частей предмета или его признаков, полученных в процессе анализа.

 

Абстрагирование – мысленное выделение одних признаков предмета и временное отвлечение от других.

 

Обобщение – мысленное объединение отдельных предметов в некотором понятии, в процессе которого человек как бы отходит от конкретного многообразия предметов, отвлекается от множества деталей, чтобы глубже познать основное, наиболее важное.

 

Указанные логические приемы образования понятий взаимосвязаны и образуют единый процесс, результатом чего является мысль, содержание которой бесконечно разнообразно, но форма неизменно одна – понятие.

 

 

Процесс образования понятий связан с процессом их обозначения, поиска точных словесных выражений мысли о предмете. Данный процесс имеет свои особенности, связанные с тем, что человек не может придумывать для каждого отдельно существующего предмета свое специфическое название. Иначе, словарный запас стал бы практически необозрим, а сам язык был бы недоступным человеку.

 

Люди вполне обходятся ограниченным количеством слов, поэтому словарный запас намного меньше числа обозначаемых с помощью слов предметов. Каждое из таких слов выражает понятия, относящиеся не к одному предмету, а к целому их классу, выделенному по совокупности общих и существенных признаков.

 

Слова-понятия позволяют человеку обобщать и углублять знания об объектах, выходя в их познании за пределы чувственного опыта. Новое знание может входить в старую систему понятий и выражаться с помощью уже известных слов. В связи с этим необходимость придумывать новые слова для выражения полученных знаний возникает редко. С помощью ограниченного числа слов, благодаря понятиям, можно обозначить практически бесконечное число предметов. Пользуясь словами для обозначения понятия о предмете, человек как бы «видит» в предмете больше, чем дано ему непосредственно через органы чувств.

 

Чтобы осмысленно оперировать понятиями, правильно их использовать в решении теоретических и практических задач необходимо уметь выявлять две основные логические характеристики: объем и содержание понятия.

Объем понятия - это совокупность (класс) предметов, которые мыслятся в данном понятии.

Содержание - совокупность признаков предмета (предметов), мыслимых в данном понятии.

Операции над понятиями - это такие логические действия, вследствие которых

создаются новые понятия.

 

11 суждение и его логическая структура

Суждение – мысль, выраженная предложением, в которой что-либо утверждается или отрицается о предметах действительности, об их свойствах, отношениях, образе действия, взаимосвязях. Суждение может соответствовать или не соответствовать действительности (быть истинным или ложным). Общая формула "S есть Р" или "S не есть Р". Виды: сложные (состоит из простых суждений или их сочетаний) и простые (состоит из понятий, можно разложить только на понятия). Простое суждение состоит из трех элементов — субъекта (понятие о предмете мысли: то, о чем говорится в данном суждении. Обозначается символом S), предиката (понятие о признаке предмета мысли: то, что говорится о предмете мысли. Обозначается символом Р), логической связки (отношении между предметом и содержанием) и квантора (указывает объем «некоторые», «все»). Среди простых суждений выделяют атрибутивные (суждения свойства– в которых указывается на наличие или отсутствие у предметов каких-либо свойств, состояний, видов деятельности и т.п.), экзистенциальные (суждения существования– в которых утверждается или отрицается существование некоторого материального или идеального объекта) и суждения с отношениями- (реляционные – суждения, в которых говорится о каких-либо отношениях между предметами). Категорическое суждение –в которых утверждение или отрицание выражается без формулирования каких-либо условий и без каких-либо вариантов. Обычно это все атрибутивные суждения. 4 типа суждений: А — общеутвердительное суждение. Структура его: «Все S есть Р», «Все люди — позвоночные». I — частноутвердительное суждение. Структура его: «Некоторые S есть Р», «Некоторые элементарные частицы имеют положительный заряд» Е — общеотрицательное суждение. Его структура: «Ни одно S не есть Р». Пример: «Ни один дельфин не является рыбой». О — частноотрицательное суждение. Структура его: «Некоторые S не есть Р». Например, «Некоторые люди не являются долгожителями». Распределенность терминов- связана с отношением их объемов. Если объем (S или Р) целиком включен в объем другого (S или Р), то он считается распределенным. Таковым же он будет считаться и в случае его полного исключения из объема второго термина. В остальных случаях термин считается нераспределенным.

 

12 состав и виды простых суждений

Суждение – мысль, выраженная предложением, в которой что-либо утверждается или отрицается о предметах действительности, об их свойствах, отношениях, образе действия, взаимосвязях.

Простое суждение состоит из трех элементов — субъекта (понятие о предмете мысли: то, о чем говорится в данном суждении. Обозначается символом S), предиката (понятие о признаке предмета мысли: то, что говорится о предмете мысли. Обозначается символом Р), логической связки (отношении между предметом и содержанием) и квантора (указывает объем «некоторые», «все»).

Виды простых суждений

1. Атрибутивные суждения или суждения свойства. В суждениях этого вида с предметом связывается наличие или отсутствие какого-либо свойства.

2. Экзистенциальные суждения или суждения существования.

Существование – это особый признак, свойство предмета быть, находиться в реальности.

3. Релятивные суждения или суждения сотношениями.

В них предикатом являются отношения, устанавливаемые между предметами.

Основными логическими характеристиками простых суждений являютсяколичество и качество.

Качество суждения зависит от связки между субъектом и предикатом и может быть либо утвердительным, либо отрицательным.

Количество суждения – характеристика, показывающая, в каком объёме входит в суждение его субъект. По количеству суждения делятся на единичные, частные и общие.

Слова "этот", "некоторые", "все" – кванторы или кванторные слова, определяющие количественную сторону суждений. Единичные суждения в логическом анализе приравниваются к общим, т.к. и те и другие связывают предикат со всем объёмом субъекта.

Суждения, в которых точно выяснены их количество и качество, называютсяпростыми категорическими суждениями.

В логике используется объединённая классификация из четырёх видов категорических суждений:

1. Общеутвердительные (А): Все S есть Р

2. Общеотрицательные (Е): Ни одно S не есть Р

3. Частноутвердительные (I): Некоторые S есть Р

4. Частноотрицательные (О): Некоторые S не есть Р

Распределённость терминов в категорических суждениях

Терминами категорического суждения называются субъект и предикат этого суждения. Термин распределён, если он рассматривается в данном суждении во всём объёме, т.е., если он полностью включается в объём другого понятия или полностью исключается из него. В противном случае термин не распределён.

В суждениях (А) субъект распределён, а предикат, как правило, не распределён. В случае, когда термины суждения являются тождественными понятиями, они оба распределены.

В суждении (I) квантор "некоторые" показывает, что субъект данного вида суждения всегда не распределён, т.к. только часть его объёма относится к предикату. Предикат, как правило, также не распределён, кроме случаев, когда объём предиката полностью входит в объём субъекта и, таким образом, предикат оказывается распределён. Этот вид суждений, где объём предиката меньше объёма субъекта, называют частными выделяющими суждениями (в отличие от общих выделяющих, где Р > S).

Суждение (Е) состоит из терминов, которые благодаря квантору "ни одно" и отрицательной связке, не имеют общих элементов объёмов. Другими словами, объём субъекта полностью исключается из объёма предиката, и наоборот – это означает, что оба термина распределены.

Суждение (О) имеет кванторное слово "некоторые", т.е. объём субъекта мыслится только частично. Предикат в этом суждении, напротив, распределён, поскольку все элементы его объёма исключены из мыслимой части объёма субъекта.

Из всех рассмотренных случаев можно вывести следующее обобщающее правило: субъект всегда распределён в общих суждениях и не распределён в частных; предикат всегда распределён в отрицательных суждениях, а в утвердительных он распределён тогда, когда объём предиката меньше или совпадает с объёмом субъекта (Р £S).

Для того, чтобы установить или проверить распределённость субъекта и предиката, можно изобразить их отношение кругами Эйлера и выделить (заштриховать) те части объёмов терминов, которые соединяются утвердительными или исключаются отрицательными высказываниями.

 

13 Распределенность терминов в суждениях

Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема.

Рассмотрим, как распределены термины в суждениях А, Е, I, О.

Суждение А (Все S суть Р). «Все студенты нашей группы (S) сдали экзамены (Р)». Субъект этого суждения («студенты нашей группы») распределен, он взят в полном объеме: речь идет обо всех студентах нашей группы. Предикат этого суждения не распределен, так как в нем мыслится только часть лиц, сдавших экзамены, совпадающая со студентами нашей группы.

Таким образом, в общеутвердительных суждениях S распреде­лен, а Р не распределен. Однако в общеутвердительных суждениях, субъект и предикат которых имеют одинаковый объем, распределен не только субъект, но и предикат. К таким суждениям относятся общевыделяющие суждения, а также определения, подчиняющиеся правилу соразмерности.

Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы (S) не является неуспевающим (Р)». И субъект, и предикат взяты в полном объеме. Объем одного термина полностью исключа­ется из объема другого: ни один студент нашей группы не входит в число неуспевающих, и ни один неуспевающий не является студен­том нашей группы. Следовательно, в общеотрицательных суждени­ях и S, и Р распределены.

 

Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы (S) — отличники (Р)». Субъект этого суждения не распре­делен, так как в нем мыслится только часть студентов нашей груп­пы, объем субъекта лишь частично включается в объем предиката:

только некоторые студенты нашей группы относятся к числу от­личников. Но и объем предиката лишь частично включается в объем субъекта: не все, а только некоторые отличники — студенты нашей группы.

Следовательно, в частноутвердительном суждении ни S, ни Р не распределены.

Исключение из этого правила составляют частновыделяющие суждения, предикат которых полностью входит в объем субъекта. Например: «Некоторые родители, и только они (S), являются много­детными (Р)». Здесь понятие«многодетные» полностью входит в объем понятия «родители». Субъект такого суждения не распреде­лен, предикат распределен.

Суждение О (некоторые S не суть Р). «Некоторые студенты нашей группы (S) — не отличники (Р)». Субъект этого суждения не распределен (мыслится лишь часть студентов нашей группы), пре­дикат распределен, в нем мыслятся все отличники, ни один из кото­рых не включается в ту часть студентов нашей группы, которая мыслится в субъекте. Следовательно, в частноотрицательном сужде­нии S не распределен, а Р распределен.

 

14 Логические отношения между суждениями. Логический квадрат

Между суждениями A, E, I, O с одинаковым терминами (с одинаковой материей) существует четыре вида отношений:

Отношение подчинения, в котором находятся суждения A и I, E и O. Суждения А и Е – подчиняющие, а суждения I и O подчинённые. Если общее суждение истинно, то истинно одинаковое и ним по материи и качеству чистое, но не наоборот. Например: суждение общее «Все люди смертны» истинно, то истинно будет и частное суждение «Некоторые люди смертны», обратное же не имеет место;

Отношение противоречия между суждениями E и I, O и A. Здесь суждения E и I, а также O и A относятся друг к другу как утверждение и отрицание. Поэтому в каждом из этих двух суждений одно является обязательно истинным, а другое 0 обязательно ложным. Например, если суждение «Все вещи имеют имя» (А) истинно, то суждение «Некоторые вещи не имеют имени» (О) будет ложным. И обратно: если суждение (О) истинно, то суждение (А) той же материи будет ложно;

Отношение контрарности между суждениями А и Е. В первом из них утверждается определённый вид отношения S к P, а именно, что объём S полностью содержится в P, а во втором, то есть в суждении Е, отрицается как этот вид отношения между S и P, так и отношение перекрещивается между объёмов S и P, то есть отношение противоположности не сводится к отрицанию одного суждения другим. Поэтому противоположные суждения могут быть одновременно ложными. Приведём пример. а) «Все соки представляют собой жидкость» и б) «Ни один сок не является жидкостью». При условии истинности одного суждения (из противоположных (контрарных) суждений) другое обязательство ложно. Другой пример: «Все книги изготовлены из бумаги» (А) и «Ни одна книга не изготовлена из бумаги» (Е). Здесь оба суждения ложны.

Так называемый, «логический квадрат» показывает все рассмотренные отношения между суждениями.

 

Определённые логические отношения существуют также между суждениями, у которых одинаковые либо только предикаты, либо только субъекты. Если суждения имеют одинаковые предикаты, то между ними существует отношение подчинения, если они имеют одно и то же качество. Например: «Все планеты светят отраженным светом» и «Юпитер светит отраженным светом». Если также суждения имеют разные качества, то они являются противоречивыми. Суждения с одинаковым субъектом противоположны, если противоположными являются их предикаты. Например: «И.Е. Репин – великий художник-реалист» и «И.Е. Репин – заслуженный художник реалист». Оба суждения истинны быть не могут, но оба могут быть ложными.

Если у двух суждений с одинаковым субъектом предикаты – совместимы понятия, то они будут согласными и могут оказаться одновременно как ложными, так и истинными. Например: «Д.И. Менделеев был выдающимся химиком» и «Д.И. Менделеев был выдающимся лектором» являются одновременно истинными. Другой пример: «Математика является главной наукой среди всех наук» и «Математика является второстепенной наукой»; оба суждения ложны.

Между суждениями совершенно разной материи логика никаких отношений указать не можем.

 

15 Модальность суждений: сущность и виды

Модальность - это явно или неявновыраженная в суждении дополнительная информация о логическом или фактическом статусе суждения, о регулятивных, оценочных, временных и других его характеристиках. Наиболее важными и распространенными выступают такие виды модальности, как алетическая, деонтическая, эпистемическая и аксиологическая. Алетическая модальность выражает характер связи между мыслимыми предметами, а следовательно, между субъектом и предикатом суждения. Модальными словами в русском языке, в этом случае, являются «возможно», «случайно» и их синонимы. С точки зрения алетической модальности различают следующие разновидности суждений: - ассерторические суждения или суждения о реальном факте. Например: «В России действительно осуществляется реформирование Вооруженных Сил». В таких суждениях модальность не выражена, констатируется лишь сам факт чего-либо; - проблематические суждения или суждения о возможности чего-либо. Например: «В России может быть осуществлено реформирование Вооруженных Сил»; - аподиктические суждения или суждения о необходимости чего-либо. Например: «В России необходимо осуществить реформирование Вооруженных Сил». Деонтическая модальность распространяется только на деятельность людей, нравственные и правовые нормы их поведения в обществе. Она выражается с помощью таких слов, как «разрешается», «запрещается», «обязательно» и т. п. В зависимости от характера норм деонтическая модальность имеет следующие разновидности: - суждения о наличии (или отсутствии) какого-либо права. Они формируются с помощью слов «разрешено», «запрещено», «вправе» и других. Например: «Каждый имеет право на свободу и личную неприкосновенность» (правопредоставляющая норма) и «Запрещаются любые формы ограничения прав граждан при вступлении в брак и в семейные отношения по признакам социальной, расовой, национальной, языковой или религиозной принадлежности» (правозапрещающая норма); - суждения о наличии (или отсутствии) какой либо обязанности. Они формулируются посредством слов «обязан», «должен», «необходимо» и др. Например: «Признание, соблюдение и защита прав и свобод человека и гражданина — обязанность государства». Эпистемическая модальность характеризует степень достоверности знания. Она выражается с помощью слов «доказано», «недоказуемо», «опровергнуто» и им подобных. Выделяют две разновидности эпистемической модальности: - суждения, основанные на вере. Например: «Верю в наступление лучшей жизни»; - суждения, основанные на знании. Например: «По показаниям свидетелей Николаев не участвовал в похищении материальных ценностей». Аксиологическая модальность выражает отношение человека к материальным и духовным ценностям. Она включает такие слова, как «хорошо», «плохо» и т. п. Например: «Безразличное отношение к государственному имуществу приводит к его утрате» или «Хорошо, что я не опоздал на занятия в институт».

 

17 построение таблиц истинности.

Построение таблиц истинности для логических функций

Логическая функция ― это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).

Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части ― соответствующие значения логической функции.

При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:

1. инверсия;

2. конъюнкция;

3. дизъюнкция;

4. импликация и эквивалентность.

Для изменения указанного порядка выполнения логических операций используются круглые скобки.

Предлагается следующий алгоритм построения таблицы истинности.
1. Определить количество наборов входных переменных ― всевозможных сочетаний значений переменных, входящих в выражения, по формуле: Q=2ⁿ, где n ― количество входных переменных. Оно определяет количество строк таблицы.
2. Внести в таблицу все наборы входных переменных.
3. Определить количество логических операций и последовательность их выполнения.
4. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.

 

Чтобы не повторить или не пропустить ни одного возможного сочетания значений входных переменных, следует пользоваться одним из предлагаемых ниже способов заполнения таблицы.

Способ 1. Каждый набор значений исходных переменных есть код числа в двоичной системе счисления, причем количество разрядов числа равно количеству входных переменных. Первый набор ― число 0. Прибавляя к текущему числу каждый раз по 1, получаем очередной набор. Последний набор ― максимальное значение двоичного числа для данной длины кода.

Например, для функции от трех переменных последовательность наборов состоит из чисел:

Способ 2. Для функции от трех переменных последовательность данных можно получить следующим путем:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю половину нулями, нижнюю половину единицами;
б) в следующей колонке для второй переменной половинку снова разделить пополам и заполнить группами нулей и единиц; аналогично заполнить вторую половинку;
в) так делать до тех пор, пока группы нулей и единиц не будут состоять из одного символа.

Способ 3. Воспользоваться известной таблицей истинности для двух аргументов. Добавляя третий аргумент, сначала записать первые 4 строки таблицы, сочетая их со значением третьего аргумента, равным 0, а затем еще раз записать эти же 4 строки, но теперь уже со значением третьего аргумента, равным 1. В результате в таблице для трех аргументов окажется 8 строк:

 

Например, построим таблицу истинности для логической функции:

Количество входных переменных в заданном выражении равно трем (A,B,C). Значит, количество входных наборов Q=2³=8.

Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов 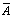и (B V C), а также искомого окончательного значения сложного арифметического выражения :

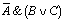A	B	C		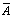B V C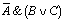

Для операций конъюнкции, дизъюнкции и инверсии определены законы булевой алгебры, позволяющие производить тождественные (равносильные) преобразования логических выражений.

Законы логики
1. А <=> A закон двойного отрицания;
2. A&B <=> B&A коммутативность конъюнкции;
3. AVB <=> BVA коммутативность дизъюнкции;
4. A&(B&C) <=> (A&B)&C ассоциативность конъюнкции;
5. AV(BVC) <=> (AVB)VC ассоциативность дизъюнкции;
6. A&(BVC) <=> (A&B)V(A&C) дистрибутивность конъюнкции относительно дизъюнкции;
7. AV(B&C) <=> (AVB)&(AVC) дистрибутивность дизъюнкции относительно конъюнкции;
8. A&A <=> A
9. AVA <=> A
10. AVA <=> И закон исключенного третьего;
11. A&A <=> Л закон непротиворечия;
12. A&И <=> A
13. AVИ <=> И
14. A&Л <=> Л
15. AVЛ <=> A
16. (A&B) <=> A V B законы де Моргана;
17. (AVB) <=> A & B
18. A => B <=> A V B замена импликации.

Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Пример 1. Упростить выражения так, чтобы в полученных формулах не содержалось отрицания сложных высказываний.
Решение

 

18 Виды сложных суждений и условия их истинности

Сложные суждения состоят из простых суждений, связанных логическими союзами: конъюнкцией, дизъюнкцией, импликацией и эквиваленцией (см. гл. 1, параграф 1.2).

Ознакомившись с простыми суждениями, мы уже знаем, что основной логической характеристикой суждения является истинностное значение. Соответственно, логический анализ суждений разворачивается по поводу их истинности или ложности. Понятно, что сделать это в сложных высказываниях значительно труднее, чем в простых. Чтобы выполнить эту задачу, нужно учесть специфику логического анализа сложных суждений. Она состоит в следующем.

1. Истинностные значения сложных суждений зависят от двух параметров: истинностных значений составляющих их простых суждений (а) и характера логических союзов (б).

Чтобы убедиться в этом, возьмем для примера два простых истинных суждения: "Пушкин убит на дуэли"; "Лермонтов убит на дуэли". Соединяя их логическим союзом "и", получаем истинное сложное высказывание: "Пушкин убит на дуэли (т) и Лермонтов убит тоже (я)". Соединяя же их строго разделительным союзом "либо-либо", получаем уже ложное высказывание: "Либо Пушкина убили па дуэли (т), либо Лермонтова (/?)".

Возьмем еще два простых суждения, — одно истинное, другое ложное, — и соединим их разными союзами:

"Пушкин — автор поэмы "Полтава"" (истинно).

"Лермонтов — автор поэмы "Полтава"" (ложно).

Соединяя союзом "и" — получим ложное высказывание: "Пушкин — автор поэмы "Полтава"" (т) и Лермонтов тоже" (я). Соединяя их строго разделительным союзом "либо-либо" — получим истинное высказывание: "Либо Пушкин — автор поэмы "Полтава" (ш), либо Лермонтов" (п).

2. В простых суждениях, входящих в состав сложных, учитываются только их истинностные значения. Внутренняя (субъектно-предикатная) структура простых суждений, а также их качество и количество не учитываются.

Возьмем шекспировские строки:

"Слова парят, а чувства к низу гнут, А слов без чувств вверху не признают".

Это сложное высказывание состоит из трех простых: "Слова парят" (т), "Чувства к низу гнут" (п), "Слов без чувств вверху не признают" (р). У каждого из них есть субъект, предикат, количественная и качественная характеристики, но при логическом анализе сложных суждений это выяснять не надо. Надо установить только одно — истинность или ложность каждого простого высказывания; а затем с учетом функций логических союзов определить истинностное значение всего высказывания. Достигается это путем построения таблиц истинности.

3. Истинностные значения сложных суждений определяют путем составления таблиц истинности. Когда с помощью логических связок мы соединяем простые высказывания в сложное, встает вопрос: при каких условиях сложное высказывание считается истинным, а при каких — ложным? Ответить на этот вопрос позволяют таблицы истинности. Каждая логическая связка имеет свою таблицу, которая показывает, при каких наборах значений логических переменных сложное высказывание с этой связкой будет истинным, а при каких — ложным.

Таблицы истинности позволяет выделить из класса формул нашего языка:

• всегда истинные формулы (тавтологии);

• всегда ложные формулы;

• установить отношение логического следования между формулами;

• их эквивалентность и т.д.

4. Надо учитывать несовпадение логических и грамматических форм: сложное суждение может быть выражено простым распространенным предложением. Например: "Любовь молчалива и разговаривает только делом" (М. М. Пришвин). С точки зрения грамматики — это простое распространенное предложение. С точки зрения логики — это сложное высказывание, состоящее из двух простых, каждое из которых может быть оценено с точки зрения истинности или ложности, а именно: действительно ли, что "любовь молчалива", и действительно ли, что она "разговаривает только делом"?

В естественном языке сложное высказывание может быть выражено простым распространенным предложением в следующих логико-грамматических формах:

а) простой субъект и сложный предикат. Примером может служить высказывание академика

В. И. Челомея (1914—1984) — выдающегося советского ученого в области механики и процессов управления: "Организовать (5) — это значит сначала оценить возможность (Р), а уже потом ставить задач)' (Р^)"- Или высказывание известного американского изобретателя Т. Эдисона (1847-1931): "Успех (5) - это 10% везения (Р,) и 90%

б) сложный субъект и простой предикат.

"Любовь (5)) и голод (52) правят миром (Р)" (Ф. Шиллер);

"Больной душе (5,) и совести усталой (52)

Во всем беды мерещится начало (Р)" (В. Шекспир);

в) сложный субъект и сложный предикат.

"Страдание (5)) и боль (52) всегда обязательны для широкого сознания (Р,) и глубокого сердца (Р)", — утверждал Ф. М. Достоевский, а Н. А. Бердяев, развивая эту мысль, заметил: "Без боли (5,) и страдания (52) в этом мире человек опустился бы (Р,) и животное в нем победило бы (Р)".

 

19 Отношения между сложными суждениями

Сопоставление сложных суждений позволяет разделить их на группу независимых и группу зависимых суждений.

К независимым относятся суждения, которые не имеют общих составляющих; для них характерны все сочетания истинных значений. Зависимые - это суждения, которые имеют одинаковые составляющие и могут различаться логическими связками, включая отрицание. Пример зависимых сложных суждений: "Норвегия или Швеция имеют выход к Балтийскому морю" и "Не верно, что Норвегия и Швеция имеют выход к Балтийскому морю". Хотя эти суждения различны по логической форме (первое из них - дизъюнктивное суждение, а второе - отрицание конъюнкции), вместе с тем они зависимы, поскольку включают одинаковые составляющие.

Сложные зависимые суждения могут быть совместимыми и несовместимыми.

Отношение совместимости.

К совместимым относятся суждения, которые одновременно могут быть истинными. Как и в случае простых суждений различают три вида совместимости сложных суждений: эквивалентность, частичная совместимость и подчинение.

Эквивалентными являются такие суждения, которые принимают одни и те же значения, т. е. одновременно являются либо истинными, либо ложными.

Отношение эквивалентности позволяет выражать одни сложные суждения через другие - конъюнкцию через дизъюнкцию или импликацию, и наоборот.

Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего, подчиненное всегда будет истинным.

Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующего все виды рассуждений.

Отношение несовместимости.

Несовместимыми являются суждения, которые одновременно не могут быть истинными. Из двух видов несовместимости одна - противоположность, другая - противоречие.

Противоположность - отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.

Противоречащими являются суждения, которые одновременно не могут быть ни истинными, ни ложными. При истинности одного из них другое будет ложным, а при ложности первого второе будет истинным.

Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию.

Сопоставление суждений в дискуссиях. Отчетливое представление об отношениях, в которых могут находиться суждения, позволяет логически грамотно анализировать высказывания участников дискуссий. Встречаются ситуации, когда логический анализ показывает совместимость различных по структуре суждений. Нередко это случается с частными суждениями. Пропонент утверждает, что "Некоторые S есть Р"; оппонент настаивает, что "Некоторые S не есть Р". На поверку же выходит, что эти суждения не исключают друг друга, а являются частично совместимыми и оба могут оказаться истинными.

В спорах и дискуссиях могут смешиваться противоречащие и противоположные суждения; Например, обвинитель утверждает, что в рассматриваемом случае имело место у

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: