Барометрическая формула

Давно известно, что давление газа над поверхностью Земли уменьшается с высотой. Атмосферное давление на некоторой высоте h обусловлено весом вышележащих слоев воздуха. Пусть на высоте h давление равно p . Тогда на высоте h + dh давление будет равно p + dp (рис. 9. 3). Разность давлений dp = dF/S, где dF = rSdhg вес столба воздуха в объеме Sdh , S - площадь основания цилиндра, r - плотность воздуха, g - ускорение земного притяжения. Отсюда получим

dp = -r·g·dh. (9. 11)

Знак минус показывает, что давление убывает с высотой. В этом выражении кроме p и h есть еще одна переменная r = m·n , где m - масса одной молекулы, n - число молекул в единице объема. Подставляя сюда выражение для n из формулы (9. 7), получим r = mp/(kT). Подставляя это выражение в формулу (9. 11), получим

dp/p = - mgdh /(kT). (9. 12)

Получили дифференциальное уравнение для p как функции от h . Положим T = const. Суммируя все dp/p в пределах от p_o до p, при соответствующем суммировании правой части, когда высота изменяется от 0 до h , приходим к определенным интегралам:

= -

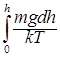
После интегрирования получим ln(p/p_o) = - mgh/(kT). Потенцируя, получим

p = p_oexp[-mgh/(kT)]. (9. 13)

Эта формула характеризует зависимость давления от высоты, и поэтому называется барометрической. Приборы, принцип действия которых основан на этой формуле, позволяют измерять высоту по давлению, которое существует на данной высоте. Эти приборы называются альтиметрами. Их применяют, например, в авиации.

В показатель экспоненты (9. 13) входит масса молекулы. Следовательно, концентрация более тяжелых молекул будет с высотой убывать быстрее. Поэтому на больших высотах уменьшается процентное содержание кислорода по сравнению с азотом. Летчики, летающие на очень больших высотах, часто пользуются кислородными масками. Спад концентрации молекул с высотой зависит также от g (от массы планеты). Чем меньше g , тем дальше от планеты уходит газ и в конце концов ее покидает, Поэтому на малых планетах, например на Луне, атмосферы нет. На планетах с большим g, например, на Юпитере, где температура атмосферы близка к абсолютному нулю, молекулы атмосферы расположены практически слоем, напоминающим земной океан.

Барометрическая формула является частным случаем распределения Больцмана. Согласно формуле (9. 7) давление пропорционально концентрации молекул n . Поэтому формулу (9. 13) можно представить в следующем виде

n = n_oexp[-mgh /(kT)], (9. 14)

где n_o - число молекул в единице объема при h = 0. На разной высоте молекула обладает различным запасом потенциальной энергии E_п = mgh . Вводя E_п в формулу (9. 14), получим

n = n_oexp[-Eп /(kT)]. (9. 15)

Больцман показал, что распределение (9. 15) справедливо не только в поле земного тяготения, но и в любом потенциальном поле любых сил для совокупности любых одинаковых частиц, находящихся в тепловом движении. В соответствии с этим распределение (9. 15) называют распределением Больцмана (по имени выдающегося австрийского физика, получившего его в 1896 г. ). Центробежное потенциальное поле сил, намного превышающих силы земного притяжения, возникает в центрифугах. Распределение (9. 15) позволяет рассчитать распределение частиц в этом поле и затем провести оптимально разделение по слоям изотопов различных элементов, мельчайших шлиф-порошков и т. д. Умножив обе части распределения Больцмана на kT,

получим со­гласно основному уравнению МКТ, что давление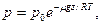

где — молярная масса, R — универсальная газовая постоянная.

Это так называемая барометрическая формула .

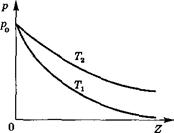Она строго спра­ведлива для идеального газа, температура которого не зави­сит от высоты (изотермическая атмосфера ).