Уравнение сухого и влажного воздуха

Влажный воздух представляет собой механическую смесь сухого воздуха и водяного пара. Поскольку критическая температура водя­ного пара (Т_кр =374 °С) выше наблюдаемых в атмосфере темпера­тур, то он в реальных условиях атмосферы может переходить в жид­кое и твердое состояния (конденсироваться).

Теория фазовых переходов водяного пара детально рассматрива­ется в разделе IV. Здесь отметим только, что условие Т < Т_кр необ­ходимо, но недостаточно для перехода пара в жидкое и твердое со­стояния. Для начала конденсации водяного пара необходимо также, чтобы он достиг состояния насыщения.

Поскольку реально наблюдаемые температуры в атмосфере ниже критической температуры водяного пара, его физические свойства, вообще говоря, могут отличаться от свойств идеального газа. Одна­ко экспериментальным путем установлено, что физические свойст­ва водяного пара практически близки к свойствам идеального газа. По этой причине уравнение состояния водяного пара с достаточной степенью точности можно записать в виде

 

 

где е — парциальное давление водяного пара; v_n — удельный объем; R_п— удельная газовая постоянная водяного пара:

 

μ _п = 18, 015 кг/кмоль — относительная молекулярная масса водяно­го пара.

Для того чтобы показать, насколько удовлетворительно уравне­ние (1. 4. 1) выполняется и для насыщенного водяного пара, приве­дем значения R_п, рассчитанные по уравнению (1. 4. 1) на основе из­меренных значений температуры Т, давления насыщенного пара Е и удельного объема v_п:

 

 

Из этих данных видно, что, строго говоря, водяной пар по своим свойствам отличается от идеального газа, поскольку R_п не постоян­на. Однако в пределах 0—40 °С экспериментальное значение R_п практически совпадает с теоретическим (461 Дж/(кг -К)). Это гово­рит о том, что в данном интервале температур с достаточной степе­нью точности уравнение (1. 4. 1) может служить уравнением состоя­ния как ненасыщенного, так и насыщенного водяного пара.

Перейдем к выводу уравнения состояния влажного воздуха. Для этого выделим в атмосфере 1 г влажного воздуха. Пусть в нем содер­жится s г водяного пара и (1 - s) г сухого воздуха. Обозначим через v_п, v_c и v удельные объемы водяного пара, сухого и влажного возду­ха соответственно. Сухой воздух и водяной пар равномерно распре­делены по всему объему влажного воздуха и полностью занимают этот объем. Поскольку v — объем водяного пара и (1 - s) г сухого воздуха, то удельные объемы водяного пара и сухого воздуха соот­ветственно равны:

 

 

 

Примем следующие обозначения: р — общее давление; Т — тем­пература, одинаковая для водяного пара, сухого и влажного возду­ха; е — парциальное давление водяного пара; (р - е) — парциальное давление сухого воздуха. Уравнением состояния водяного пара слу­жит уравнение (1. 4. 1). Уравнение состояния сухой части воздуха имеет вид

 

Составим отношение:

 

Или

 

 

Подставим в уравнения (1. 4. 1) и (1. 4. 3) значения удельных объе­мов в соответствии с (1. 4. 2) и удельной газовой постоянной водяного пара в соответствии с (1. 4. 4):

 

 

Сложив уравнения (1. 4. 5) и (1. 4. 6), получим уравнение состоя­ния влажного воздуха:

 

 

которому можно придать два различных вида в зависимости от того, отнесен ли множитель (1 + 0, 608s) к удельной газовой постоянной Rc или к температуре Т.

Если ввести удельную газовую постоянную влажного воздуха

 

 

то уравнение (1. 4. 7) примет вид

 

 

Удельная газовая постоянная R в этом уравнении — величина переменная, зависящая от влажности воздуха s.

В метеорологии множитель (1 + 0, 608s) обычно относят к темпе­ратуре, вводя понятие виртуальной температуры

 

 

Нередко виртуальную температуру представляют в виде суммы:

 

 

где ∆ T_v — виртуальный добавок. Из сравнения последнего выраже­ния с (1. 4. 9) следует:

 

 

Если водяной пар находится в состоянии насыщения, то ∆ T_v при данных Т и р достигает наибольшего значения

 

 

которое при фиксированном р является функцией одной лишь тем­пературы. При р = 1000 гПа максимальный виртуальный добавок ∆ T_vт имеет следующие значения:

 

 

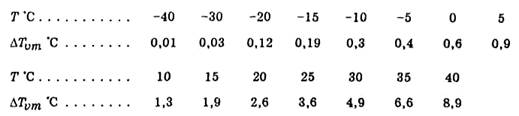
Из этих данных вытекает, что виртуальный добавок, а соответствен­но и роль влажности в изменении плотности воздуха малы при низ­ких температурах и достаточно велики при высоких.

С введением виртуальной температуры уравнение состояния влажного воздуха принимает вид

 

 

Если в (1. 4. 11) ввести плотность влажного воздуха p = l/v, то уравнение состояния влажного воздуха примет вид

 

 

Из сравнения уравнения (1. 4. 12) с уравнением (1. 3. 8) следует, что при одинаковых температуре и давлении плотность влажного воздуха всегда меньше плотности сухого воздуха. Физически это объясняется тем, что в состав влажного воздуха входит более лег­кий по сравнению с сухим воздухом водяной пар, который вытес­няет часть сухого воздуха.

 

 

 

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: