Больцман обобщил свой закон на случай распределения, зависящего от внутренней энергии E молекулы (атома).

Больцман обобщил свой закон на случай распределения, зависящего от внутренней энергии E молекулы (атома).

Известно, что величина E в этом случае может принимать лишь дискретный ряд дозволенных значений, и соответствующее распределение Больцмана записывают так:

.

где 1 и 2— два произвольных (интересующих нас) уровня (состояния),

— отношение числа частиц на этих уровнях, которым отвечают внутренние энергии и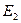

g — кратность вырождения каждого уровня. Например, кратность вырождения

- энергетического уровня атома водорода с главным квантовым числом n равна g = 2n²;

- кратность вырождения колебательного уровня двухатомной молекулы g = 1, а у вращательных уровней g = 2r+1, где r — вращательное квантовое число.

БАРОМЕТРИЧЕСКАЯ ФОРМУЛА

Формула определяет зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру Т и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), Б. ф. имеет следующий вид:

р p 0exp [- g m. ( h - h0 ) /RT ](1),

где р - давление газа в слое, расположенном на высоте h, p0 - давление на нулевом уровне ( h h0 ), m - молекулярная масса газа, R - газовая постоянная, Т - абсолютная температура. Графически зависимость (1) представлена на рис. Из Б. ф. (1) следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

n n0 exp [- mg ( h-h0 ) /kT ],

где m - масса молекулы, k - Больцмана постоянная.

Б. ф. может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Больцмана статистика ). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 применил Б. ф. к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.

Б. ф. показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина - mg ( h-h0 ) /kT, определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной kT. Чем выше температура Т, тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести mg (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести mg может изменяться за счёт двух величин: ускорения g и массы частиц m.

Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Реальное распределение давления и плотности воздуха в земной атмосфере не следует Б. ф., т. к. в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.

Б. ф. лежит в основе барометрического нивелирования - метода определения разности высот D h между двумя точками по измеряемому в этих точках давлению ( p1 и p2 ). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Б. ф. записывается в этом случае в виде: D h 18400T (1+a t ) lg ( p 1/ p 2) (в м ), где t - средняя температура слоя воздуха между точками измерения, a - температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0, 1-0, 5% от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.

Пусть атмосфера находится в состоянии покоя по отношению к земной поверхности. Такое состояние атмосферы называется ста­тическим. Тогда горизонтальная составляющая градиента давле­ния G₂ должна обращаться в нуль (в противном случае под влияни­ем этой силы воздух придет в движение). Для этого необходимо и достаточно, чтобы изобарические поверхности совпадали с уровенными.

Выделим в атмосфере две изобарические поверхности, располо­женные на высотах z и z + dz (рис. 3. 1). Давление на этих поверхно­стях обозначим через р и р + dp.

Между изобарическими поверхностями р и р + dp выделим объем воздуха с горизонтальными основаниями 1 м². На ниж­нее основание выделенного объема воздуха действует сила давления р, направлен­ная снизу вверх; на верхнее основание — сила давления

 

р + dp, направленная сверху вниз. * Силы давления, действующие на боковые грани объема воздуха, взаимно уравновешиваются.

Кроме сил давления, на объем воздуха действует сила тяжести Р, равная по модулю

 

 

и направленная сверху вниз (по вертикали).

Спроектируем все силы, действующие на выделенный объем воз­духа, на положительное направление вертикали г, вдоль которой действует (в отрицательном направлении) сила тяжести. Сумма этих проекций равна

 

 

Поскольку выделенный объем воздуха находится в покое, вектор­ная сумма всех действующих на объем сил, т. е. их результирую­щая, и сумма проекций этих сил на любое направление должны тождественно обращаться в нуль:

 

 

Подставив вместо Р его выражение по соотношению (3. 2. 1), по­лучим уравнение статики атмосферы**:

 

 

Разделив левую и правую части (3. 2. 4) на dz, определим второй вид основного уравнения статики атмосферы:

 

Величина -dp/dz = G₁ представляет собой вертикальную состав­ляющую градиента давления. В случае статического равновесия G₂ = 0, поэтому G₁ равно полному градиенту давления: G₁= G. Пра­вая часть (3. 2. 5) представляет собой силу тяжести, действующую на единичный объем воздуха, масса которого равна ρ. Таким образом, уравнение статики физически выражает собой равновесие двух сил — градиента давления и силы тяжести.

 

Из уравнения статики атмосферы можно сделать три важных вывода.

 

* Сила давления — вектор, направление которого совпадает с нормалью к повер­хности (внутрь объема). Давление воздуха — скаляр, равный отношению модуля силы давления к элементарной площади, на которую эта сила действует.

** Это уравнение справедливо и для гидросферы.

 

1. Если высота возрастает (dz > 0), то в правой части (3. 2. 4) стоит произведение только положительных множителей: gpdz > О. Поэто­му и левая часть (3. 2. 4) также больше нуля:

 

 

Таким образом, увеличению высоты (dz > 0) всегда соответствует отрицательное приращение давления (dp < 0). Это означает, что в атмосфере давление всегда убывает с увеличением высоты. Вывод о том, что этот закон справедлив всегда, вытекает из того, что уравне­ние статики выполняется с высокой степенью точности и в случае движения атмосферы.

2. Выделим в атмосфере вертикальный столб воздуха с попереч­ным сечением 1 м² и высотой от данного уровня z до верхней грани­цы атмосферы z_a. Вес этого столба обозначим через Q. Поскольку

вес элементарного столба высотой dz равен gpdz (pdz — масса эле­ментарного столба), то вес всего столба

 

Проинтегрировав правую и левую части (3. 2. 4) в пределах от z, где давление р, до z_a, где давление равно нулю (по определению вер­хней границы), получим:

 

Таким образом, приходим ко второму определению понятия дав­ления. Атмосферное давление, или давление воздуха, на каждом уровне равно весу столба воздуха единичного поперечного сечения и высотой от данного уровня до верхней границы атмосферы.

Полученное следствие делает физически ясным и вывод об убы­вании давления с высотой: увеличение высоты приводит к уменьше­нию вертикальной протяженности вышележащей части столба воз­духа и, следовательно, к уменьшению давления (по сравнению с ни­жележащими уровнями). В закрытых (негерметизированных) поме­щениях давление на каком-либо уровне практически не отличается, согласно закону Паскаля, от давления вне помещения на том же уровне.

3. Уравнение статики позволяет сделать выводы и относительно скорости убывания давления с высотой. Согласно (3. 2. 4), при подъеме на одну и ту же высоту (dz = const) уменьшение давления (-dp) тем больше, чем больше плотность воздуха р и ускорение свободного падения g. Основную роль играет плотность воздуха. С увеличением высоты плотность воздуха, как правило, убывает. Это означает, что чем выше расположен уровень, тем меньше убывание давления при подъеме на одну и ту же высоту dz.

Если точки Аи В расположены на одной и той же изобарической поверхности, то плотность воздуха в точках А и В будет зависеть только от температуры воздуха в этих точках. Если Т_А > T_В, то (при р — const) в соответствии с уравнением состояния р_А < р_В. Это, в свою очередь, означает, что при подъеме на одну и ту же высоту (dz = const) понижение давления в точке А с более высокой темпера­турой меньше, чем в точке В с более низкой температурой.

Таким образом, приходим к следующему выводу: при увеличе­нии высоты на одно и то же значение относительно некоторой изоба­рической поверхности понижение давления в более холодной воз­душной массе больше, чем в теплой массе, т. е. в холодной воздуш­ной массе давление убывает с высотой быстрее, чем в более теплой. Подтверждением этого вывода является тот факт, что на высотах (в средней и верхней тропосфере) в холодных воздушных массах пре­обладает низкое, а в теплых — высокое давление.

Оценим значение вертикального градиента давления G₁. При нор­мальных условиях вблизи уровня моря р = 1, 29 кг/м³, g = 9, 81 м/с². Подставив эти значения в (3. 2. 5), найдем:

 

 

Таким образом, вблизи уровня моря при подъеме на 100 м давле­ние убывает примерно на 12, 5 гПа. Это значение изменяется в зави­симости от температуры и давления. При увеличении высоты значе­ние G ₁ уменьшается.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: