Теоретическое обоснование метода D-разбиений

Теоретическое обоснование метода D-разбиений

Изменение параметров САУ, например, с целью оптимизации, приведет к изменению коэффициентов уравнения динамики. Останется ли при этом САУ устойчивой - неизвестно. Критерии устойчивости об этом ничего не говорят. Рассмотрим метод определения границ допустимых изменений параметров, при которых САУ не теряет устойчивости.

Приведем характеристическое уравнение замкнутой САУ к виду:

D(p) = pⁿ + c¹ p^{n -1} + c² p^n-2 +... + cⁿ = 0,

где c⁰ = a⁰ /a⁰ = 1, c¹ = a¹ /a⁰ и т. д. При некоторых конкретных значениях c¹, c²,..., cⁿ уравнение имеет единственное решение, то есть единственный набор корней ( p¹, p²,..., p_n ). По их расположению на комплексной плоскости можно судить об устойчивости САУ при заданных параметрах. Если изменить какой-либо параметр САУ, например коэффициента передачи, то изменятся и коэффициенты характеристического уравнения D(p) = 0 и станут равными c^н1, c^н2,..., c^нn. Уравнение примет вид:

Dн(p) = pn + cн1 pn -1 + cн2 pn -2 +... + cнn = 0.

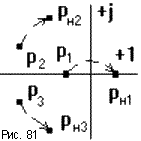Это уже другое уравнение и оно также имеет единственное решение (p^н1, p^н2,..., p^нn ), отличающееся от (p¹, p²,..., pⁿ ). Если плавно менять значение параметра САУ, то коэффициенты уравнения тоже будут плавно изменяться, а его корни будут перемещаться по комплексной плоскости (рис. 81).

Каждый уникальный набору коэффициентов c¹, c²,..., cⁿ можно изобразить точкой в пространстве коэффициентов, по осям которого откладываются значения коэффициентов c¹, c²,..., cⁿ. Так уравнению третьей степени соответствует трехмерное пространство коэффициентов (рис. 82). Пусть точка N с координатами (c_N1, c_N2, c_N3) соответствует уравнению, имеющему решение (p_N1, p_N2, p_N3), точка M с координатами (c_M1, c_M2, c_M3) соответствует уравнению, имеющему решение (p_M1, p_M2, p_M3). При изменении какого-либо параметра САУ коэффициенты характеристического уравнения будут изменяться, при этом точка в пространстве коэффициентов, соответствующая данному уравнению будет перемещаться по некоторой траектории, например из положения N в положение M. Этому перемещению будет соответствовать и перемещение корней (p_N1, p_N2, p_N3) на комплексной плоскости в положение (p_M1, p_M2, p_M3) (аналогично рис. 81).

При этом движении некоторые корни будут переходить через мнимую ось комплексной плоскости из левой полуплоскости в правую и наоборот. В момент перехода такой k -й корень примет значение p_K = j _K, а коэффициенты уравнения будут иметь определенные значения c_K1, c_K2, c_K3, определяющие в пространстве коэффициентов точку K. Подставим корень p_K в характеристическое уравнение, получим тождество:

D(pK ) = (j K)3 + cK1(j K)2 + cK2 (jK ) + cK3 = 0

Меняя w от - до + , и находя при каждой частоте все возможные сочетания коэффициентов c¹, c²,..., cⁿ , удовлетворяющих уравнению

D(j ) = (j )ⁿ + c¹ (j )^n-1 + c² (j )^n-2 +... + cⁿ = 0,

можно построить в n -мерном пространстве коэффициентов сложную поверхность S, разделяющую его на области, называемое D -областями. Полученное уравнение называется уравнением границы D -разбиения.

Переход из одной D -области в другую через поверхность S соответствует переходу одного или нескольких корней через мнимую ось в плоскости корней. То есть каждая точка внутри определенной D -области соответствует уравнению с определенным количеством левых и правых корней. Поэтому области обозначают D(m) по числу m правых корней.

Достаточно взять любую точку в пространстве коэффициентов и найти для нее число правых корней. Затем, двигаясь по пространству коэффициентов через границу S, можно выявить обозначения всех других областей. Особый интерес представляет область D(0), которой соответствуют уравнения с полным отсутствием правых корней, называемая областью устойчивости. Описанный метод определения областей устойчивости называется методом D -разбиений.

Не обязательно строить сложную n -мерную картину D -разбиения, можно изменять значения, например, только двух коэффициентов, оставляя другие коэффициенты постоянными. Границу D -разбиения S можно строить не только также и в пространстве конкретных параметров системы, от которых зависят данные коэффициенты.