 |
19. Качества работы САУ. Общие положения о качестве работы
|
|
|
|
19. КАЧЕСТВА РАБОТЫ САУ
ОБЩИЕ ПОЛОЖЕНИЯ О КАЧЕСТВЕ РАБОТЫ
Факт устойчивости или неустойчивости САУ говорит лишь о том, что переходная или свободная составляющая процесса регулирования с течением времени расходится или затухает, но такой анализ не дает ответа на такие важные вопросы как: быстрота затухания переходного процесса, форма кривой процесса регулирования и т. д. Поэтому следует отметить, что теория устойчивости является необходимым, но не достаточным условием практической пригодности САУ. Любая такая система кроме устойчивости должна еще обладать и требуемым качеством работы. Качество работы систем автоматики характеризует точность ее работы как в установившемся так и переходном режимах. Иными словами можно отметить, что качество работы системы автоматики характеризует точность воспроизведения системой задающего воздействия.
Проблема качества систем автоматики может быть поставлена как задача анализа, т. е. оценка уже спроектированной САУ или как задача синтеза, т. е. проектирование САУ заранее оговоренными показателями качества. При рассмотрении таких задач будем полагать, что САУ описывается системой дифференциальных уравнений с постоянными коэффициентами. При изменении воздействия 
на входе системы выходную величину 
можно записать:
,
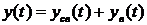где - решение дифференциального уравнения, описывающего движение САУ;
- общее решение, соответствующее однородному дифференциальному уравнению. В случае отсутствия кратных корней зависит от вида корней характеристического уравнения;
- вынужденная или установившаяся составляющая переходного процесса, обуславливаемая законом изменения .
|
|
|
Качество работы системы автоматики можно оценить по виду переходного процесса и по его составляющим и . В связи с чем различают две группы показателей качества:
1) показатели качества переходного процесса ;
2) показатели качества, характеризующие вынужденную составляющую и определяющие точность воспроизведения предписанной величины.
Показатели качества, определяемые непосредственно по кривой переходного процесса называют прямыми оценками качества, косвенные оценки качества не требуют нахождение кривой переходного процесса. Косвенные методы разделяют на: корневые, интегральные и частотные.
Показатели качества систем управления. Требование устойчивости для системы относится к числу необходимых, но не может считаться достаточным. Система может быть устойчивой, но время затухания настолько велико или ошибка в установившемся режиме настолько большая, что практически данная система не может быть использована. Поэтому система должна быть не только устойчивой, но иметь определенный переходный процесс, а ошибки в установившихся режимах не должны превышать допустимых.
Характер переходного процесса линейной системы в отличие от устойчивости зависит не только от параметров системы, но и от вида возмущающего (задающего) воздействия и начальных условий. Чтобы сравнивать системы по характеру переходного процесса, из возможных воздействий выбирают типовые или наиболее неблагоприятные и определяют кривую переходного процесса при нулевых начальных условиях. В качестве типовых воздействий обычно принимают единичное ступенчатое воздействие, единичный импульс, линейно нарастающее и синусоидальное воздействие. Для большинства систем наиболее неблагоприятным является воздействие вида единичной ступенчатой функции t) =1(t). Реакция системы на единичное ступенчатое воздействие при нулевых начальных условиях называется переходной функцией системы. Для следящих систем обычно рассматривают переходную функцию H(t), вызванную изменением задающего воздействия 1(t), а для систем стабилизации - переходную функцию Hf(t), вызванную изменением возмущающего воздействия f(t).
|
|
|
Точность системы в установившихся режимах оценивается с помощью статических и динамических ошибок. Эти ошибки по аналогии можно назвать показателем качества системы в установившихся режимах. Совокупность показателей качества переходного процесса и установившихся режимов называется показателями качества системы в целом.
Считается, что система обладает требуемым качеством, если ее показатели качества не превышают заданных значений, определенных назначением системы.
|
Рис. 4. 5. 1 |
Рассмотрим поведение системы управления (рис. 4. 5. 1), предназначенной для решения задачи слежения - соблюдения заданного закона изменения выходной переменной y(t). Последнее выражается в виде целевого условия
y(t) → у*(t), (t) → 0, (4. 5. 1)
(t) = y*(t) - у(t),
где (t) - ошибка (рассогласование) системы. При ненулевых начальных рассогласованиях система должна с течением времени обеспечить с некоторой степенью точности совпадение входного (задающего) y*(t) и выходного y(t) сигналов (устранение ошибки (t)).
Мгновенное устранение возникающих рассогласований (t) в реальных системах невозможно в силу инерционности систем регулирования и ограничений, накладываемых на управляющие воздействия. Практически неосуществимо и абсолютно точное выполнение асимптотических условий (4. 5. 1) в силу действующих возмущений и дестабилизирующих факторов. Указанные соображения приводят к необходимости введения специальных показателей качества, характеризующих эффективность решения той или иной задачи управления.
Выходная переменная возмущенной системы определяется суммой свободных и вынужденных составляющих движения:
y(t) = yсв(t) + yв(t),
где в силу устойчивости системы выполняется условия
yсв(t) → 0, yв(t) → yу(t), (4. 5. 2)
Условия (4. 5. 2) соответствуют переходному режиму системы, по окончанию которого система " переходит" в установившийся режим yy(t).
|
|
|
В зависимости от свойств системы переходный режим может оказаться достаточно быстрым или медленным, монотонным или колебательным. Для оценки поведения системы в переходном режиме вводятся динамические показатели качества, т. е. численные оценки быстродействия и колебательности системы (время переходного процесса, затухание, перерегулирование, и пр. ).
Наиболее просто оценить качество переходного режима автономной системы, для которой вынужденная составляющая отсутствует. В установившемся режиме выходная переменная системы в идеальном случае должна быть идентична задающему воздействию, что соответствует нулевому значению установившейся ошибки.
Существует ряд универсальных приемов, позволяющих одновременно оценить динамические и/или точностные показатели системы, к которым относятся методика оценки качества по переходной функции, оценка по интегральным критериям и т. д.
|
Рис. 4. 5. 2. |
Показатели качества переходного процесса. Переходная функция системы оценивается с помощью совокупности характеристик, называемых показателями качества переходного процесса. Принято использовать следующие стандартные показатели качества переходного процесса, отражённые на типичном графике 1 переходного процесса в следящей системе со ступенчатым задающим воздействием (рис. 4. 5. 2):
· tпп - время переходного процесса, по истечении которого отклонение управляемой величины y(t) относительно заданного значения yзад по абсолютному значению становится (и остается в дальнейшем) меньше определенной заданной величины уст. Обычно принимается уст = yзад, = 0. 05. Время регулирования характеризует быстроту затухания переходного процесса.
· tу - время установления, промежуток времени, за который управляемая величина в первый раз достигает своего установившегося значения, характеризует скорость процесса управления.
· уст - установившаяся ошибка (статическая точность, уст = e(∞ ) =1- ууст. ). Если уст=0, то система астатическая.
|
|
|
· σ % - относительное перерегулирование (σ = (ymax-yзад)/yзад). Обычно требуют, чтобы значение σ было менее 18%. Перерегулирование характеризует колебательные свойства процессов. При нулевом значении процесс носит монотонный характер (график 2 на рис. 4. 5. 2), а при достаточно больших приближается к незатухающему колебательному движению.
· n - число колебаний за время переходного процесса (≤ 3шт. ).
Как известно (и следует из выражения (4. 1. 11), чем дальше полюсы характеристического уравнения системы находятся от границы устойчивости (слева от мнимой оси комплексной плоскости), тем выше скорость протекания переходных процессов в системе. Для количественной оценки быстродействия систем используется также понятие степени устойчивости, которой называется положительное число, соответствующее расстоянию от мнимой оси до ближайшего к ней корня pi:
min Re pi. i = [1, n].
В общем случае, этому условию соответствует пара комплексно сопряженных корней
p1, 2 = - ± j,
c соответствующей наиболее медленной колебательной составляющей:
yi(t) = A exp(- t) sin( t+ ).
Отсюда, по затуханию колебательного процесса exp(-at) нетрудно определить время переходного процесса по заданной величине :
tпп ≈ (1/ ) ln(1/ ).
Знак приближенности в данном случае отражает тот факт, что другие составляющие общего решения (4. 1. 11) также могут внести определенную долю в значение tпп, особенно, если вещественные части их полюсов близки по значениям к минимальному значению .
По переходной характеристике и значению установившейся ошибки (ошибки при t> > tпп) можно оценить точность системы в режиме стабилизации - при постоянном входном или заданном воздействии у*(t)=const.
Эти показатели связаны с запасами устойчивости по амплитуде и по фазе. Поэтому, обеспечение стандартных показателей качества обеспечивает необходимую устойчивость. Задачу обеспечения показателей можно рассмотреть как оптимизационную. Как правило, эта задача оказывается многокритериальной и достаточно трудной для решения, в том числе, численного.
При синтезе САУ в системе обычно выделяются неизменяемая часть и изменяемая часть, в которую можно вносить коррективы. Неизменяемая часть системы задает возможность получения гарантированного качества. Классическим методом повышения качества системы является метод диаграмм В. В. Солодовникова. Практическая задача оптимизации обычно выполняется с использованием корректирующих устройств.
|
|
|
