 |
18. Устойчивость систем обладающих запаздыванием
|
|
|
|
где - значение коэффициента, при котором модуль частотной передаточной функции разомкнутой системы равен единице и система находится на границе устойчивости. В том случае если, то система уходит за пределы устойчивости.
Запас устойчивости по фазе  измеряется по дуге окружности единичного радиуса между отрицательной частью
измеряется по дуге окружности единичного радиуса между отрицательной частью 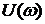 и ближайшей точкой пересечения окружности с годографом Найквиста.
и ближайшей точкой пересечения окружности с годографом Найквиста.
Определение устойчивости по логарифмическим частотным характеристикам может быть осуществлено достаточно простым способом. Необходимо на совмещенных логарифмических частотных характеристиках построить вертикальные проекции между осью абсцисс и значением -180º которые проведены через точки  и А. В результате чего получим:
и А. В результате чего получим:

 - запас по амплитуде.
- запас по амплитуде.
Запасы устойчивости влияют не только на работоспособность (устойчивость) системы, но также характеризуют качество работы системы. В реальных системах обычно  = 15…20 дБ,
= 15…20 дБ,  = 30…50º.
= 30…50º.
18. УСТОЙЧИВОСТЬ СИСТЕМ ОБЛАДАЮЩИХ ЗАПАЗДЫВАНИЕМ
Значительное число объектов сельскохозяйственного назначения описываются математической моделью, в состав которой входит звено транспортного запаздывания, при этом общая передаточная функция такой системы состоит из произведения передаточной функции линейной части системы и передаточной функции звена транспортного запаздывания
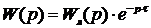
Частотная передаточная функция в данном случае может быть записана в виде:
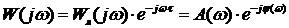 ,
,
где - АЧХ линейной части;
- ФЧХ системы с учетом звена транспортного запаздывания.
Звено чистого запаздывания не изменяет амплитуду АФЧХ, но создает дополнительный отрицательный сдвиг по фазе, зависящий от частоты  . Устойчивость САУ с запаздыванием наиболее просто определить по критерию Найквиста, при этом АФЧХ такой системы строится следующим образом: сначала строят годограф
. Устойчивость САУ с запаздыванием наиболее просто определить по критерию Найквиста, при этом АФЧХ такой системы строится следующим образом: сначала строят годограф 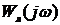 , а затем каждую i-тую точку годографа доворачивают на угол
, а затем каждую i-тую точку годографа доворачивают на угол 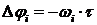 по часовой стрелке.
по часовой стрелке.
|
|
|
Оценку устойчивости систем с запаздыванием можно также выполнить используя логарифмический частотный критерий.
Очень часто анализируя устойчивость рассмотренных систем необходимо бывает установить значение запаздывания при котором система находится на границе устойчивости. Такое время носит название критического времени запаздывания и оно определяется из следующего выражения:
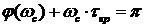
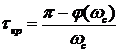
18. МЕТОД D-РАЗБИЕНИЯ
На практике бывает необходимо знать не только запас, который можно оценить с помощью какого - либо критерия устойчивости, но и всю область устойчивости по параметрам. Этой цели служит метод D - разбиения, позволяющий построить такую область в плоскости одного или двух параметров.
Рассмотрим сначала этот метод для одного параметра D, который входит в характеристическое уравнение системы линейно:
| A(p) = N(p) + D M(p) = 0. | (4. 38) |
В (4. 38) заменим p на j 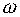 и получим уравнение
и получим уравнение

| (4. 39) |
соответствующее границе устойчивости согласно критерию Михайлова (условие (4. 24)). Разрешим его относительно D
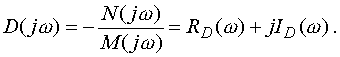
| (4. 40) |
Полученное комплексное представление параметра D позволяет изобразить его в виде вектора на плоскости 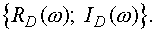 Конкретное численное значение D(j
Конкретное численное значение D(j 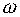 ) зависит от частоты, и при изменении
) зависит от частоты, и при изменении 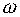 в диапазоне от -
в диапазоне от - 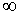 до +
до + 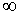 конец вектора выписывает на комплексной плоскости кривую D - разбиения, представляющую собой границу устойчивости (ее можно рассматривать также как отображение мнимой оси плоскости корней).
конец вектора выписывает на комплексной плоскости кривую D - разбиения, представляющую собой границу устойчивости (ее можно рассматривать также как отображение мнимой оси плоскости корней).
 Риc. 4. 24. Иллюстрация построения кривой D - разбиения
Риc. 4. 24. Иллюстрация построения кривой D - разбиения
| Эта кривая симметрична относительно вещественной оси, поэтому достаточно построить ее часть, соответствующую положительным значениям частоты, а вторую часть получить отображением относительно вещественной оси. |
Кривая D разбивает плоскость параметра на несколько областей с различным условием устойчивости, для определения которого необходимо выбрать по одному значению D в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при выбранном D, то она будет устойчива и при других значениях из этой области.
|
|
|
Обычно в качестве параметра D фигурирует реальный параметр системы (коэффициент передачи, постоянная времени, момент инерции и так далее), который может иметь только вещественные значения. Представление его комплексным выражением D(j 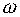 ) носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.
) носит формальный характер, а область устойчивости ограничивается отрезком вещественной оси.
Метод D - разбиения применим и в случае построения области устойчивости для двух параметров  и
и  , которые входят линейно в характеристическое уравнение
, которые входят линейно в характеристическое уравнение
A(p,  ) = 0. ) = 0.
| (4. 41) |
В этом случае уравнение границы устойчивости
A(j 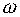 , ,  ) = 0 ) = 0
| (4. 42) |
распадается на два независимых уравнения, соответствующих равенству нулю вещественной и мнимой части (4. 42)
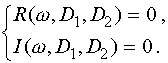
| (4. 43) |
Эти два уравнения параметрически задают кривую D - разбиения. Область устойчивости определяется аналогично случая одного параметра D.
Пример 4. 8.
Определить область устойчивости системы по коэффициенту усиления.

Рис. 4. 25. Структурная схема системы
Определим передаточную функцию замкнутой системы

и запишем ее характеристическое уравнение

Здесь k - параметр, по которому строится область устойчивости, поэтому обозначим его через D. Разрешим характеристическое уравнение относительно D и сделаем замену 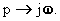 В результате получим уравнение для кривой D - разбиения:
В результате получим уравнение для кривой D - разбиения:

Вычислим значения вещественной и мнимой части D(  ) при конкретных положительных значениях частоты и занесем их в таблицу.
) при конкретных положительных значениях частоты и занесем их в таблицу.

Для построения кривой D - разбиения при отрицательных значениях частоты полученную половину D(j 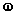 ) отобразим относительно оси абсцисс.
) отобразим относительно оси абсцисс.
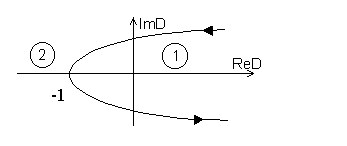
Риc. 4. 26. Кривая D - разбиения для исследуемой системы
Как видим, кривая D - разбиения разделила плоскость параметра на две области. Выбираем по одному вещественному значению D в каждой из них и оцениваем устойчивость системы второго порядка, необходимым и достаточным условием устойчивости которой является положительность всех коэффициентов характеристического уравнения. Следовательно, первая область - есть область устойчивости (-1 < k <  ).
).
|
|
|
|
|
|


