 |
17. Частотный критерий устойчивости.
|
|
|
|
17. ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ.
Критерий Михайлова
Все частотные критерии, в том числе и критерий Михайлова, основаны на хорошо известном из курса высшей математики «Принципа аргумента», который позволяет отобразить необходимое условие устойчивости на частотной плоскости.
Все элементарные вектора 
изображаются на комплексной плоскости. Задаваясь изменением частоты 
от 
до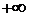 
будем наблюдать поворот единичных векторов. Анализ их изменения показывает, что устойчивые вектора поворачиваются отлично от неустойчивых. Такое наблюдение позволило сделать четкий вывод о значении угла поворота устойчивой системы в зависимости от числа правых и левых корней (левыми считаются устойчивые корни, а правыми – неустойчивые корни).
Этот частотный критерий устойчивости был сформулирован в 1938 г. советским ученым Михайловым и является интерпретацией принципа аргумента, позволяя судить об устойчивости системы наблюдая за поведением кривой называемой кривой Михайлова.
За основание построения кривой берется характеристический полином вида:
| (3. 17) |
Произведя замену 
получим характеристический полином Михайлова:
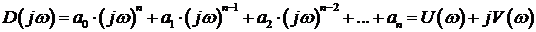(3. 18)
| (3. 19) |
При изменении частоты вектор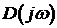 
будет изменяться как по величине, так и по направлению, описывая своим окончанием некоторую кривую, называемую кривой Михайлова или годографом Михайлова.
Для устойчивых систем кривая Михайлова начинаясь при 
на вещественной положительной полуоси, при увеличении частоты , описывает относительно начала координат некую линию.
Критерий Михайлова: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы кривая или годограф Михайлова при изменении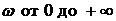 
начинаясь при на вещественной полуоси, обходила только против часовой стрелки последовательно n-квадрантов комплексной плоскости, нигде не обращаясь в нуль (n – степень характеристического полинома (уравнения)).
|
|
|
Устойчивые САУ:
Неустойчивые САУ:
Нейтральные САУ (граница устойчивости):
Анализируя кривую Михайлова можно вывести следствие из него: при прохождении кривой Михайлова числа квадрантов комплексной плоскости, происходит последовательное поочередное пересечение действительной и мнимой соей, т. е.:
| (3. 20) (3. 21) |
Значение частот при которых происходит пересечение кривой с вещественной или мнимой осью, должны является корнями уравнений (3. 20) и (3. 21), причем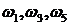 
корни уравнения (3. 21), а 
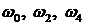- корни уравнения (3. 20). При этом корень с большим индексом по значению, также больше корня с меньшим индексом, то обязательно должно выполняться следующее неравенство:
| (3. 22) |
В связи с выше записанным следствие кривой Михайлова можно сформулировать следующим образом: САУ будет устойчивой тогда и только тогда, когда вещественная 
и мнимая 
функции Михайлова приравненные к нулю, имеют все действительные и перемеживающиеся корни, причем общее число корней равно n и при выполняется следующее условие:
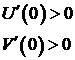
| (3. 23) |
Для реализации этого следствия определяются только корни уравнения 
. Перемежаемость корней можно проверить подставив в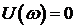 
найденные корни . Знаки значений при подстановке возрастающих по значению корней должны чередоваться (+ - + - + и т. д. ). Если что-то не так – система является неустойчивой.
|
|
|
