 |
Тақырып №1. Кіріспе. Кодтардың шығу тарихы
|
|
|
|
Тақ ырып №1. Кіріспе. Кодтардың шығ у тарихы
Мә ліметтерді кодтау ерте заманнан бері жү зеге асып келе жатыр. Юлий Цезарьдың мә ліметтерді кодтауы жә не Геродоттың жазғ ан мысалдарынан осыларды анық байқ ауғ а болады. Бертін келе мә ліметтерді кодтаумен кө птеген ғ алымдар мен философтар айналысқ ан. Осығ ан сә йкес ә ртү рлі жазулар жә не криптограммалар ө те кө п кездеседі.
Негізінен мә ліметтерді кодтау кө п жағ дайда белгілі бір адамның ғ ана білетін қ ұ пия ісі болғ ан. Бірақ қ азір уақ ытта дә лелденіп отырғ анына байланысты алғ ашқ ы қ ұ рылғ анғ ан криптограммалардың барлығ ын, негізінен, шешуге болады. Американың атақ ты ғ алымы, кодтау теориясының негізін қ алаушы Шеннон мынадай тұ жырым дә лелдеген. Егер нақ ты кілті болмаса, ешқ ашанда шешілмейтін криптограмма қ ұ руғ а болады. Қ азіргі заманда криптограммамен бірге криптоанализ де жақ сы дамығ ан. Алғ ашқ ы кодтау мысалының бірі – Морзе ә ліппесі. Онда ә рбір ә ріп, нү кте мен сызық шаның жиынынан тұ рады. Осы қ асиетті Бода деген ғ алым телеграфта пайдаланғ ан. Мұ нда нү кте мен кідірістің кө мегімен қ ашық тытағ ы адамғ а мә лімет жіберуге болады. Информацияны 0 мен 1 бойынша кодтау кесіндіні қ ақ қ а бө лу теориясына байланысты шық қ ан. Мысалығ а, 0-ден 7-ге дейін кез-келген бір санды жасырып, табуымыз қ ажет болсын. Санды табу ү шін неше рет сұ рақ қ ою керек. Бұ л жерде санды табу ү шін 3 сұ рақ қ ою жеткілікті болып табылады. Оларды сә йкес 0 жә не 1 арқ ылы ө рнектеуге болады.
|
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0000 | 001 | 010 | 011 | 100 | 100 | 110 | 111 |
Егер алынғ ан аралық ү лкен болса, оғ ан сә йкес 0 мен 1 сандарының тізбектері де кө бейеді. Бірақ 0 жә не 1 арқ ылы кез-келген санды кодтауғ а болады.
Негізгі ә дебиеттер: [1, 2, 5, 8]
Қ осымша ә дебиеттер: [11, 12]
Тақ ырып №2. Информацияның ө лшемдері
Кез келген бізге берілетін хабарламаның біз ү шін ең маң ызды мінездемесі ондағ ы берілген информация болып табылады. Мысалы, таң ертең кү н шық ты. Сіздің ү йің із қ ұ лап қ алды. Мұ ндағ ы екінші сө йлемде, біз ү шін, кө п информация берілген. Берілген хабарламадағ ы информация мө лшері оның кездесу немесе жү зеге асу ық тималдығ ына байланысты болады. Біз информацияны бит жә не байт арқ ылы ө рнектейміз. Берілген бит ық тималдық теориясымен қ алай байланысқ анын қ арастырайық. Ық тималдық теориясында тиынғ а байланысты классикалық мысал бар. Берілген тиынды n рет лақ тырып, герб жағ ының тү су ық тималдығ ын анық тайды. Бұ л жағ дайда мү мкіншілікті 4 бит арқ ылы ө рнектейік. Мү мкіншілік болатын ә р тү рлі жағ дайлар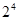 
тең. Осындай жағ дайдың болуы 1/16 –ге тең болады.
Анық тама: Информация мө лшері деп І=-log (p) мә нін атаймыз. І-информация мө лшері, р -ық тималдық болу жағ дайы. log – негізі екі, екілік логарифм, минус таң басы (-) –информация мө лшерінің оң болуына ә сер етеді, себебі ық тималдық теориясы бойынша оқ иғ аның ә рқ ашанда болу ық тималдығ ының махсималь мә ні max=1 болады.
Информация ө лшемінің ең кіші ө лшем бірлігі бит екенін білеміз. Бізге екі информация берілсін: 0 немесе 1 жә не олардың ық тималдық тү су жағ дайы бірдей болсын.
|
|
|
Р (0) = P(1)=1/2
Бір цифр ү шін информацияның ө лшемін анық тайық.
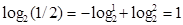бит.
Мысалы, Латын алфавитінде 26 ә ріп бар, сондық тан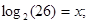 
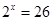, яғ ни бұ дан 
.
Цифрлар ү шін 10=> 
Негізгі ә дебиеттер: [1, 2, 6, 9]
Қ осымша ә дебиеттер: [11, 12]
Тақ ырып №3. Энтропия
Берілген символдардың оқ иғ а пайда болу ық тималдығ ы ә р тү рлі болсын.
P(0)=p P(1)=q=1-p
Онда осығ ан байланысты бір цифрда болатын информация мө лшері ә р тү рлі болады. Мысалы,
P (0)=0, 99 P(1)=0, 01
Осыларды логарифмдеу арқ ылы информация мө лшерін анық тайық.
- 
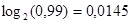бит І=- 
Ұ зындығ ы n-ге тең хабарлама берілсін. Онда 0 жә не 1сандары кездеседі. Орташа алғ анда 0 саны p*n кездессе, онда 1 саны q*n=n-p*n q*n=n*(1-p) кездеседі.
Ә рбір цифрдағ ы информация мө лшерін білгеннен кейін ұ зындығ ы n-ге тең хабарламадағ ы жалпы информация мө лшері қ анша болатынын анық тауғ а болады. Бізде 0 –дің тү су ық тималдығ ы р, 1-дікі 1-р.
-р*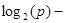 
q*n* 
n-жалпы ұ зындық, барлығ ын n-ге бө лсек орташа мә нін табамыз. Яғ ни біз бір символғ а келетін орташа информация мө лшерін анық таймыз.
Біздің алфавиттерде N ә ртү рлі символдар болсын жә не олардың пайда болу ық тималдығ ы сә йкесінше p(1), p(2), …., p(n) болса, онда бір символғ а сә йкес келетін орташа информация мө лшері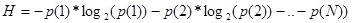 
Осы Н-тың мә нін берілген символдар ағ ынындағ ы энтропия деп атаймыз.
Мысалы: 1) Екі символды алфавит берілсін, яғ ни олардың кездесу ық тималдығ ы ½ тең. Бұ л жағ дайда энтропия 1 бит символғ а тең. 2) егер р(0)=0, 99 p(1)=0, 01 бұ л жағ дайда энтропия 0, 08 бит символғ а тең болады, бірақ бұ л шығ арылғ ан есептерде берілген ағ ындағ ы символдар бір-біріне тә уелсіз, яғ ни келесі символдардың пайда болуы алдындағ ы символғ а тә уелсіз болып келеді. Энтропия ұ ғ ымымен бірге информацияның шамадан тыс артық болу ұ ғ ымы ө те тығ ыз байланысты. Мысалы: берілген хабарламада символдардың мө лшері шамадан тыс кө п болуы мү мкін. Бірақ соғ ан қ арамастан олардың ә келетін информация мө лшері ө те аз болуы мү мкін.
|
|
|
0 0 0
1 1 1 болса информация мө лшері 1.
Максималдық энтропиядан ағ ымдағ ы энтропияны азайтып max энтропияғ а бө лу арқ ылы артық информацияны білуге болады.
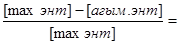[шамадан тыс артық болу]
Негізгі ә дебиеттер: [1, 2, 9]
Қ осымша ә дебиеттер: [11, 12
|
|
|
