 |
Тақырып№10. Циклдық кодтар.
|
|
|
|
Тақ ырып№10. Циклдық кодтар.
Жалпы сызық тық кодтардың ішінде циклдық кодтар, сипатталуы жә не қ олданылуы қ арапайым болғ андық тан, ең маң ызды кодтар болып табылады. Сондық тан циклдық кодтар кө птеген маң ызды есептерді шығ ару барысында жиі қ олданылады. Мұ нда сызық тық кодтағ ы кодтау жә не декодтау жағ дайлары қ ысқ а тү рде беріледі. Декодтаудың, циклдық коды, ү шін ең бір қ арапайым жә не оң ай ә дісі бар. Бұ л жерде декодтау ә дісін толық мең геру ү шін алгебра курсының аппараты қ ажет.
1) Векторды цикл бойынша жылжыту.

 ө рісі.
ө рісі.
 - циклдық жылжыту.
- циклдық жылжыту.
Мысал: (0 1 1 0 1) (1 0 1 1 0) (0 1 0 1 1)
Циклдық код дегеніміз- ө зінің векторы мен бірге цикл бойынша жылжытуды қ амтитын сызық тық код, яғ ни кез келген кодтық вектордың цикл бойынша жылжытып алынғ ан векторы кодтық вектор болып табылады. Циклдық кодтарды қ арастыру барысында векторлар ү шін қ олданылатын амалдар мен бірге мына амалды қ арастырамыз: ә рбір векторғ а оның циклдық ығ ысуын сә йкес қ оямыз. Мұ нда векторларғ а сә йкес кө пмү шені алып, соларды қ арастырып, зерттеу ө те ың ғ айлы болып табылады.
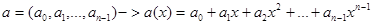 (2)
(2)
Енді a векторы ү шін а(х) кө пмү шелерін қ арастырып зерттейміз.

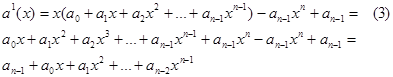
(3)-ден келесі шығ ады. Егер х- тің n-дә режесі циклды қ ұ растырудың элементі болса, онда хn =1. (4)
Егер (4) орындалса, онда 1, х, х2,..., хn-1 элементтері ә р тү рлі жә не сызық тық тә уелсіз болады. Бұ л жағ дайда х-тің дә режесін кө бейту n модулі бойынша жү зеге асырылады, яғ ни
|
|
|
xk xm = xr (5)
r =k+ m (mod n)
n=5, k=3, m=4, r =2
(3)-ге (4) –ті қ олданамыз, онда а1(х)=xa(x) циклдық жылжыту кез келген векторды х-тың мә ніне кө бейту арқ ылы алынады. (4) пен (5) –ті пайдаланып дә режесі n-1 –ден аспайтын кез келген екі кө пмү шелікті кө бейту ережесін қ арастырайық:
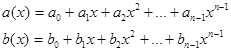
1-ші вектордың ә рбір элементін 2-ші вектордың барлық элементтеріне кө бейтіп шығ амыз, жә не х-дің дә режесін кө бейтуде (4) –ші тең дікті қ олданамыз.
Негізгі ә дебиеттер: [1, 2]
Қ осымша ә дебиеттер: [12]
Тақ ырып №11. Қ анық қ ан кодтар. Кодтарды бағ алау
Қ анық қ ан кодтарда кодтық сө здердің саны 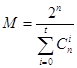 (1)
(1)
Егер де n= 2t+1, => M= 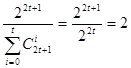
Ұ зындығ ы 2m -1-ге тең Хеммингтың коды берілсін. Мұ ндай кодтар кез- келген бір қ атені жө ндейтінін білеміз. Сонымен
n= 2m-1, t=1, V= 


m=3, n=7, M=16.
(4)-ші тең дік бойынша екілік қ анық қ ан кодтар ү шін  тү рінде ө рнектелуі керек.
тү рінде ө рнектелуі керек.
1949 жылы Голей (23, 12) кодын қ ұ растырды. Бұ л қ анық қ ан код жә не ол ү ш қ атені жө ндейді. 1957 жылы Эллой қ анық қ ан кодтарды зерттеп, зерттеу барысында комплекс сандарды, дифференциялдық тең деулерді қ олданып берілген теорияны алгебралық тең деулер жү йесіне алып келді.
Бізге ұ зындығ ы n- ге тең сө здер берілсін. Олардың ішіндегі кодтық сө здің ең кіші ара қ ашық тығ ы d -ә ріпімен берілсін. Осы ұ зындығ ы n-ге тең сө здің ішінен кодтық сө здің санын қ алай анық тауғ а немесе бағ алауғ а болады. Оны біз M(n, d) деп белгілейміз. 
 (1)
(1)
Бұ л формулада егер де r кез келген бір радиус болса, онда 

|
|
|
Негізгі ә дебиеттер: [1, 2, 9]
Қ осымша ә дебиеттер: [11, 12]
Тақ ырып №12. Архиваторлар. Лемпель – Зив тә сілі
Архиваторлар мағ ынасына байланысты 2 тү рлі болады.
1) сығ у архиваторы программа бойынша 2-лік мә ліметтерді ө лшемі аз файлғ а жазу.
2) архивтегі файлдарды қ алпына келтіру.
Информацияларды сығ у алгоритмдерді жалпы 2 тү рге бө леді.
1) информацияны жоғ алтпай сығ атын алгоритмдер.
2) Информацияның кейбір мә ліметтерін жоғ алтып, сығ атын алгоритмдер.
І-ші алгоритмдер бойынша сығ ылғ ан информацияны тү гелдей қ алпына келтіруге болады. Олардың мысалдары arj, pk zip, rar, ha, т. б.
ІІ-ші алгоритмдер бойынша алғ ашқ ы информация тек жуық тап қ алпына келтіруге болады. Мұ ндай сығ у мә тіндік файлдар ү шін тиімді болып табылмайды. Бірақ оларды дыбыс, графика, видеоинформацияларды сақ тау барысында ө те жиі қ олданады. Мысалы: jpeg файлы.
Егер берілген ағ ында барлық символдар бірдей мү мкіншілікпен жә не бір-біріне байланыссыз болса, онда мұ ндай ағ ындардың символдарын сығ у мү мкін емес. Сондық тан кез-келген файлды сығ уғ а болатын архиватор қ ұ растыру мү мкін емес. Мә ліметтерді архивтеу барысында мә ліметтер тізбегінің ағ ынының ерекшеліктерін қ арастырады. Ә зірше, біз ағ ындағ ы символдардың алдың ғ ы символдарғ а тә уелділігін қ арастырайық. Кодтау теориясында келесі символдардың алдынғ ы символдарғ а тә уелділігін сипаттау қ иын мә селелердің бірі болып табылады. Нақ ты программада бұ л есепті басқ аша қ ояды. Оны қ ысқ арту деп атайды.
Онда бұ ғ ан дейін кездескен символдардың орнына файлғ а сол символдарғ а сә йкес сілтеме жасалады. Практикада бұ л тө мендегідей жү зеге асырылады.
1) Белгілі бір мә ліметтердің тізбегінен басқ а алфавитте символдар қ ұ растырылады. Бұ л жағ дайда мү мкіншілік болғ анша қ ысқ арту ә дісін пайдаланады. Мұ нда Леппель-Зив алгоритмінің ә р-тү рлі варианттарын қ арастырады.
2) Алдынғ ы қ ұ рылғ ан алфавит бойынша Хаффман немесе арифметикалық кодтау ә дістері бойынша есептерді шығ ару. Мұ нда ә рбір символдың пайда болуы ық тималдығ ы ә р тү рлі жә не келесі символдың пайда болуы алдың ғ ы алдың ғ ы символғ а тә уелсіз болады.
|
|
|
Бұ ғ ан дейін қ арастырғ ан тә сілдің барлығ ында алғ ашқ ы берілген алфавит элементінің саны шектеулі болғ ан. Ә детте белгілі бір тілге байланысты онда қ олданылатын негізгі символдардың саны 256-дан аспайды. Осындай алфавиттерді қ олдану арқ ылы, мысалы Хаффман коды, 2-рет жү ргізілген алгоритм мә тінді 50%- ке дейін сығ уғ а мү мкіндік береді. Мә тінді ә рі қ арай жақ сы сығ у ү шін берілген алфавиттен белгілі бір қ айталанатын мә тіндерді мү мкіндігінше бө ліп алып, соларғ а сілтеме жасау арқ ылы орындауғ а болады. Осындай тә сілдің бірі Лемпеь –Зив тә сілі. Тә сілдің негізгі жұ мыс істеу принцпі. Жұ мыс істеу барысында алгоритм сө здік қ ұ растырады. Ө зі оқ итын мә тіннің ішінен сө здікке тиісті элементтерді іздей бастайды. Егер оны табатын болса, оғ ан екі мә нді сә йкес қ ояды. Табылғ ан ішкі жолдың ұ зындығ ын сол сө зден оқ ылатын мә тінге дейін қ ашық тық. Егер ондай элемент табылмаса, онда келесі оқ ылатын символды сө здікке тіркейді. Осылай жұ мыс жалғ аса береді. Яғ ни алгоритм бойынша мә ліметтердің ағ ынына екі мә н сә йкес қ ойылады.
Length - ұ зындық.
Distance- ара қ ашық тық.
Сонымен кез-келген мә ліметтер ағ ынын жаң а алфавитте белгілеп алады. L, D
0, 1
A-900 І-460
Ә -31 Ө -83
Б-112 Ң -104
В-0 Ү -62
Г-48 Ұ -40
Ғ -56 Қ -240
Д-212 Һ -2
Е-208 Ж-148
Негізгі ә дебиеттер: [3, 9]
Қ осымша ә дебиеттер: [11, 13]
|
|
|
|
|
|


