 |
Тақырып №7. Алмастыру тәсілі
|
|
|
|
Тақ ырып №7. Алмастыру тә сілі
Алғ ашқ ы мә тіннің символдарының ретін ғ ана ө згертетін шифрды алмастыру шифры деп атаймыз.
Ұ зындығ ы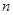 
символдан тұ ратын хабарламаны шифрлеуге арналғ ан алмастыру шифрының тү рлендіруін қ арастырайық. Оны тө мендегі кесте тү рінде беруге болады:
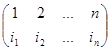
(2)
мұ ндағ ы 
- таң далғ ан тү рлену кезіндегі алғ ашқ ы хабараламаның бірінші ә ріпіне тү сетін шифрмә тіннің орнының нө мірі. 
- екінші ә ріп ү шін орын жә не т. б. Кестенің жоғ арғ ы жолында рет-ретімен 1-ден 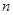-ге дейінгі сандар жазылғ ан, ал тө менгі жолында сол сандар, бірақ кез - келген ретпен алынғ ан. Мұ ндай кесте 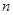дә режелі алмастыру деп аталады.
Берілетін тү рлендірудің алмастыруын біле отырып, мә тінді шифрлеумен бірге оның шифрын қ алай шешуге болатынын орындауғ а болады. Мысалы, егер тү рлендіру ү шін
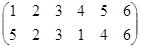
ауыстыруы қ олданылса жә не сонымен бірге МОСКВА сө зі шифрленсе, онда КОСВМА шығ ады. НЧЕИУК хабарламасын шифрлең із.
Ұ зындығ ы 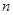-ге тең хабарламаны шифрлеу ү шін арналғ ан ауыстыру шифрының ә р тү рлі тү рлендіру саны 
-дан артық болмайды. Алғ ашқ ы 10 натурал сан ү шін мә нінің кестесін келтірейік:
|
| ||||||||||
|
|
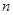
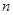ү лкен болғ анда -ды жуық тап есептеу ү шін ө зімізге белгілі Стирлинг формуласын қ олдануғ а болады.
Негізгі ә дебиеттер: [3, 6, 10]
Қ осымша ә дебиеттер: [12, 13]
Тақ ырып №8. Периодты кілтпен берілген кө п алфавитті ауыстыру шифры
|
|
|
Орыс тілінің 30-ә ріпті алфавитін қ арастырайық:
АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯ.
Бұ л алфавитте Ё, Й жә не Ъ ә ріптері қ атыспайды, олар орыс тілінде ашық хабарлама қ ұ руғ а қ атыспайды. Шынында да, Ё ә ріпін Е ә ріпіне ауыстыру, Й ә ріпін И ә ріпіне ауыстыру, ал Ъ ә ріпін Ь ә ріпіне ауыстыру осы алфавитті қ олдану арқ ылы жазылғ ан ашық хабарламаның мағ ынасын тү сінуге мү мкіндік береді.
Кез - келген тілдегі алфавитте ә ріптер рет-ретімен орналасады. Бұ л алфавитте ә рбір ә ріптің реттік нө мірін иемденуге мү мкіндік береді. Келтірілген алфавитте А ә ріпі 1 реттік нө мірге ие, ал О ә ріпіне – 14 ретті, Ы ә ріпіне – 27 ретті нө мірді сә йкес береміз. Егер ашық хабарламада ә рбір ә ріпті оның алфавитте қ арастырылғ ан нағ ыз реттік нө мірімен ауыстырсақ, онда сандық хабарламаның тү рленуі алғ ашқ ы ашық хабарламаны тұ рғ ызуғ а мү мкіндік береді. Мысалы, 1 11 20 1 3 9 18 сандық хабарлама ә ріптік хабарламағ а тү рленгенде АЛФАВИТ деген сө зді білдіреді.
Алфавитте нағ ыз ә ріптер ретін қ осымшалайық. Алфавиттегі соң ғ ы ә ріпнің соң ынан бірінші ә ріп шығ ады. Егер ә ріптерді сағ ат тілімен орналастырсақ, онда осындай ә ріптер реті орындалады. Мұ ндай орналасу кезінде ә рбір ә ріпке ө зінің ретті нө мірін меншіктеуге болады. Мұ ндай нө мірді сә йкесінше ретті нө мір деп атаймыз. Егер алфавиттегі ә ріптер саны 
-ке тең болса, онда берілген ә ріптегі реттік нө мір сә йкесінше 0-ден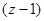 
-ге дейінгі мә ндерді қ абылдайды жә не осығ ан қ атысты есептеледі.
Негізгі ә дебиеттер: [3, 6, 10]
Қ осымша ә дебиеттер: [11, 13]
Тақ ырып№9. Сызық тық кодтар
Алдыың ғ ы қ арастырылғ ан кодтардың барлығ ына тә н мынадай қ асиет бар: екі кодтық сө здің қ осындысы немесе айырмасы кодтық сө з болып табылады. Енді осы қ асиет арқ ылы жалпы бір теория қ ұ руғ а болады. Ол ү шін F ө рісін аламыз. Ө рістегі ә рбір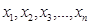 
сө зге 
n ө лшемді кең істікте 
векторларын сә йкес қ оямыз жә не оны код деп атаймыз. Осығ ан сә йкес тексеру шарттарын
|
|
|
(1) 
шығ арып аламыз.
Егер код (1)-ді қ анағ аттандырса, оны жұ птық қ асиетке тексерілген код деп атайды.
(1)-дің шешімдерінің мынадай қ асиеті бар:
1. Егер а жә не b (1) –дің шешімі болса, онда а+b да (1)-ң шешімі болады.
2. 
(1)- шешімі болсын, онда 
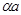-да (1)-дің шешімі болады. Бұ дан шығ атын қ орытынды: жұ птық қ а тексерілген кодтар сызық тық кең істік қ ұ райды. Мұ ндай кең істіктерді сызық тық кодтар деп атайды. Берілген кең істігінде ішкі кодтық кең істіктердің ө лшемі k-ғ а тең болса, ол (n, k) сызық тық коды деп аталады.
Сызық тық кодтар - кодтау теориясында негізгі кодтардың бірі. Оның тө мендегідей негізгі қ асиеттері бар:
- қ атені тез табу, оны оң ай жө ндеуге болатындығ ы.
- жазылатын кодтың қ ысқ алығ ы.
Сызық тық кодтар практикада жиі қ олданылады. Ә рбір кодтық сө зге F ө рісінде белгілі бір матрицаны сә йкес қ оюғ а болады. Мұ ндай матрицаны (1)-дің кө мегімен қ ұ растыруғ а болады:
Матрицадағ ы жолдар – сызық тық тә уелсіз болып табылады.
Негізгі ә дебиеттер: [1, 2, 4]
Қ осымша ә дебиеттер: [11, 12]
|
|
|
