 |
Функции и Тендеулер. YYYYYYYYYYYY
|
|
|
|
Матрица
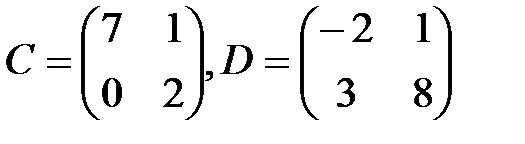
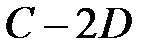 матрицасынын мә ні: B)
матрицасынын мә ні: B) 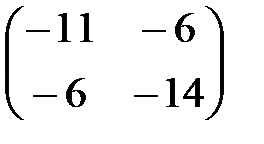 D)
D) 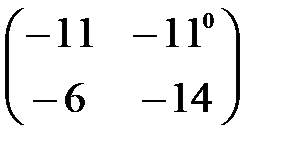 E)
E) 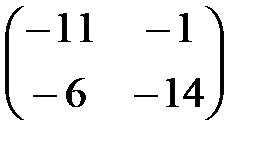
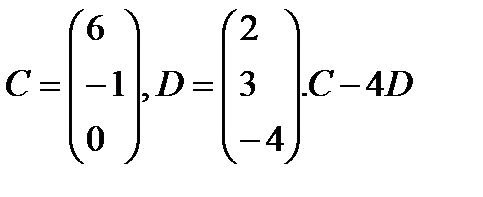 матрицасын табу керек: C)
матрицасын табу керек: C) 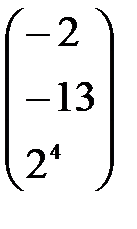 E)
E) 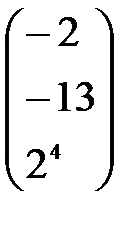
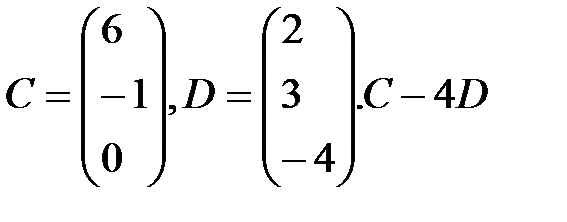 матрицасының мә ні: A)
матрицасының мә ні: A) 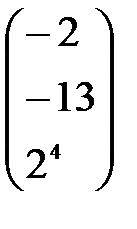 C)
C)  F)
F) 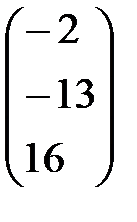
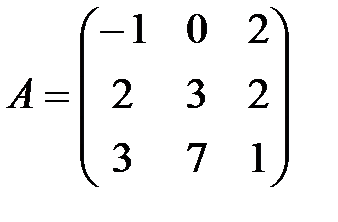 ,
,  A+B матрицасынын мә ні: B)
A+B матрицасынын мә ні: B) 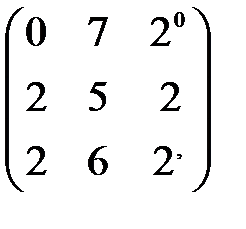 E)
E) 
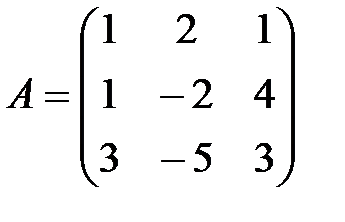 ;
; 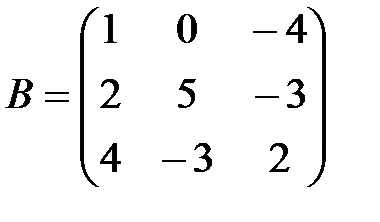 A+B матрицасының мә ні: A)
A+B матрицасының мә ні: A) 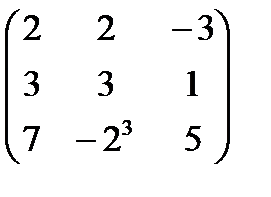
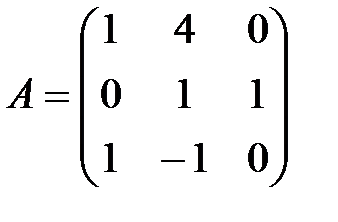 матрицасының рангі: А) 3 В) 2-ден артық.
матрицасының рангі: А) 3 В) 2-ден артық.
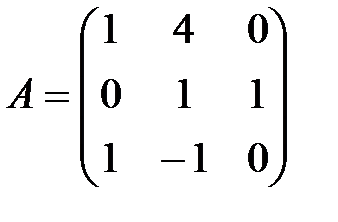 матрицасының рангы: A) 1-ден артық C)2-ден артық
матрицасының рангы: A) 1-ден артық C)2-ден артық
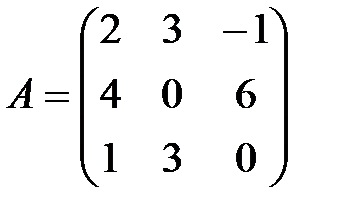 матрицасы берілген.
матрицасы берілген. 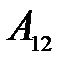 алгебралық толық тауышты есептең із: A) 6 B) 18/3
алгебралық толық тауышты есептең із: A) 6 B) 18/3
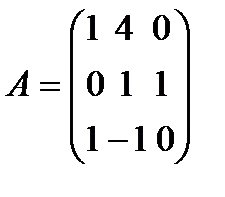 матрицасының рангы: А)3 В)2-ден артық
матрицасының рангы: А)3 В)2-ден артық
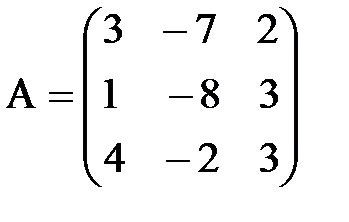 ,
, 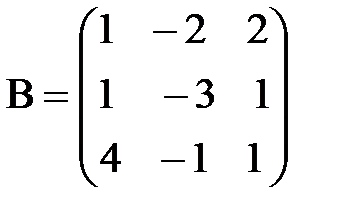 . 3А+2В матрицаларын табу керек; A)
. 3А+2В матрицаларын табу керек; A) 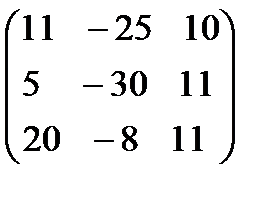 B)
B) 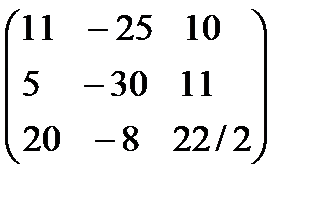 C)
C) 
 ,
,  . А+В матрицаларын табу керек; A)
. А+В матрицаларын табу керек; A) 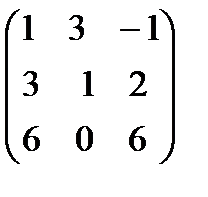 B)
B) 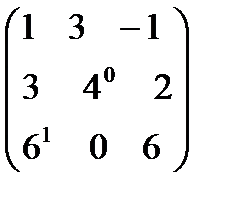 C)
C) 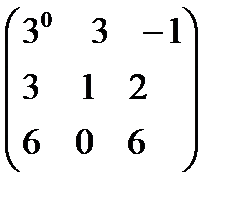
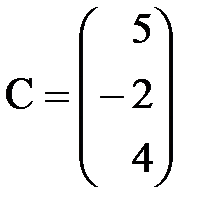 ,
, 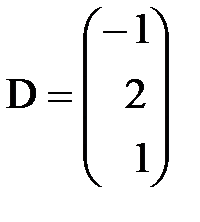 . С–2D матрицаларын табу керек; A)
. С–2D матрицаларын табу керек; A) 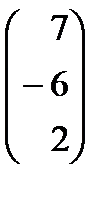 B)
B)  C)
C) 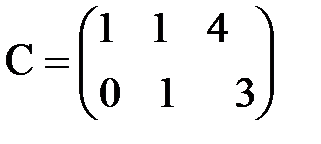
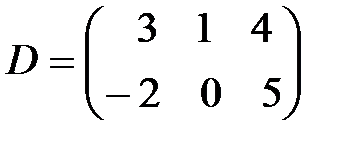 . С–4D матрицаларын табу керек; A)
. С–4D матрицаларын табу керек; A) 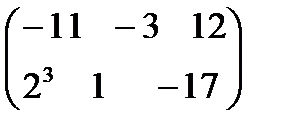 B)
B) 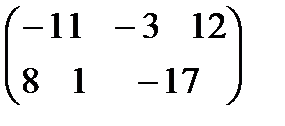 C)
C) 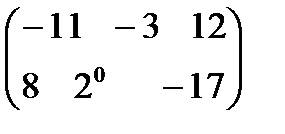
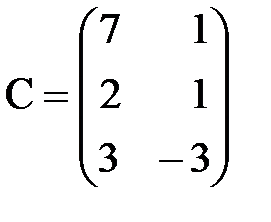 ,
, 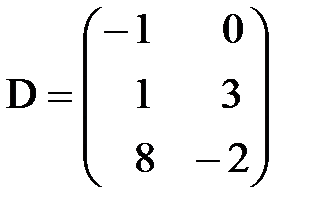 . С–D матрицаларын табу керек; A)
. С–D матрицаларын табу керек; A) 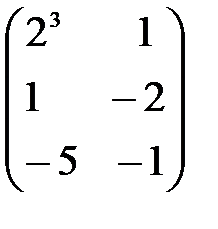
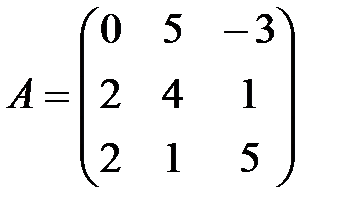 ,
, 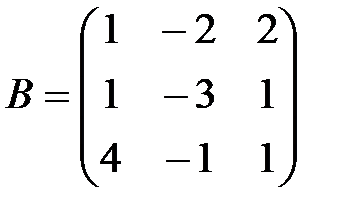 , А+В матрицасын табу керек: А)
, А+В матрицасын табу керек: А) 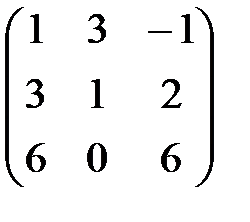 В)
В) 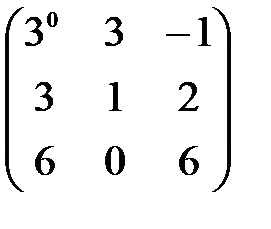 С)
С) 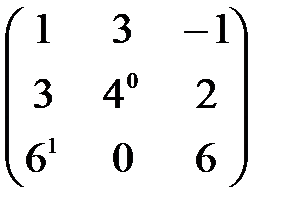
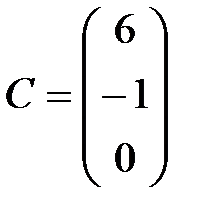 ,
, 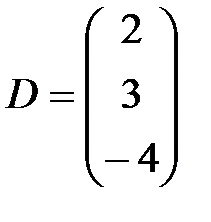 , С-4D матрицасын табу керек: А)
, С-4D матрицасын табу керек: А) 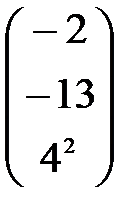
 ,
, 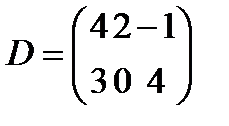 C-2D Матрицасын табу керек: А)
C-2D Матрицасын табу керек: А) 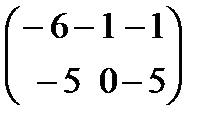
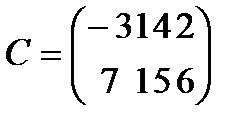 ,
, 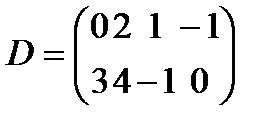 C-DМатрицасын табу керек: А)
C-DМатрицасын табу керек: А) 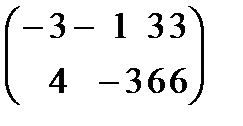
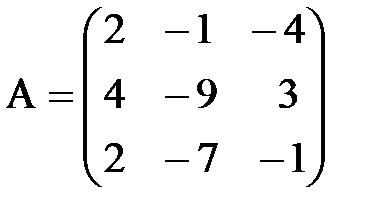 ,
, 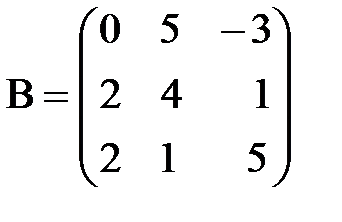 . А+В матрицаларын табу керек; A)
. А+В матрицаларын табу керек; A) 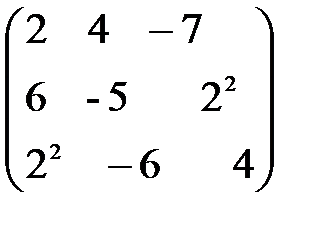
 ,
, 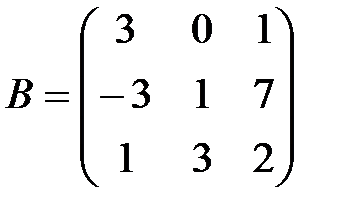 . А+В матрицасын табу керек. А)
. А+В матрицасын табу керек. А) 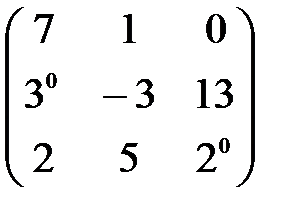 В)
В) 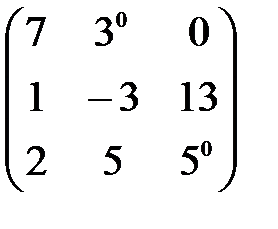
 ,
, 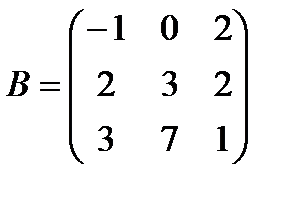 . А+В матрицасын табу керек А)
. А+В матрицасын табу керек А) 
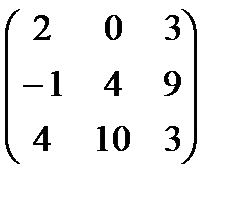 В)
В) 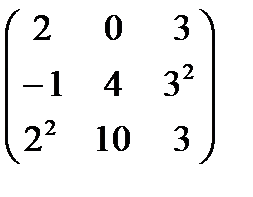
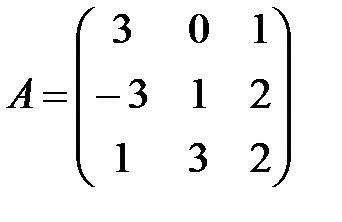 ,
, 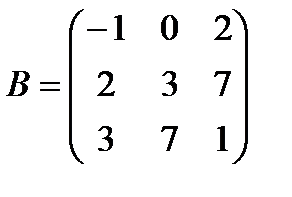 . А+В матрицасын табу керек А)
. А+В матрицасын табу керек А) 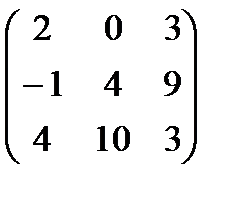 В)
В) 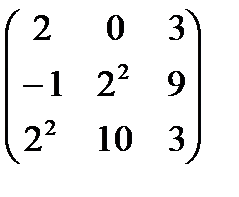
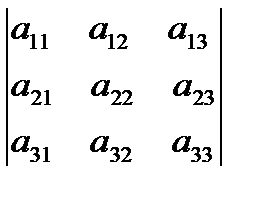 анық тауышы тең: А)
анық тауышы тең: А) 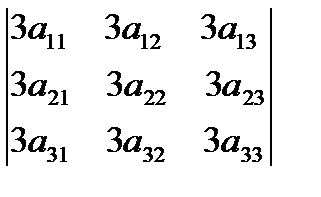
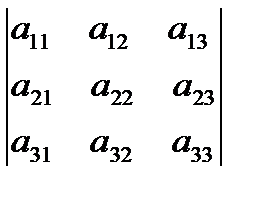 анық тауышы тең: А)
анық тауышы тең: А) 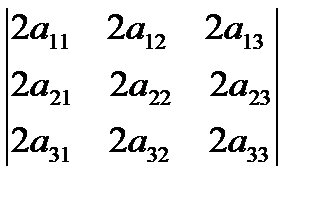
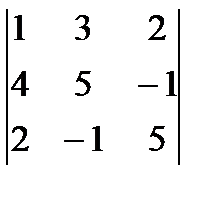 анық таушыныі мә ні A )
анық таушыныі мә ні A )  B)
B) 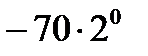
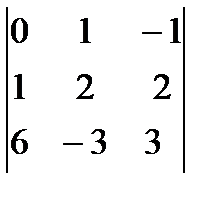 анық таушыныі мә ні C)
анық таушыныі мә ні C)  E)
E) 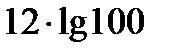 G)
G) 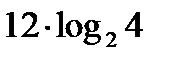
 анық тауышын былайша есептеуге болады: B)Анық тауыштын қ андайда бір жолының элементтері арқ ылы жіктеу жолымен D) Анық тауыштын қ андайда бір бағ анының элементтері арқ ылы жіктеу жолымен E)Саррюс ережесі бойынша
анық тауышын былайша есептеуге болады: B)Анық тауыштын қ андайда бір жолының элементтері арқ ылы жіктеу жолымен D) Анық тауыштын қ андайда бір бағ анының элементтері арқ ылы жіктеу жолымен E)Саррюс ережесі бойынша
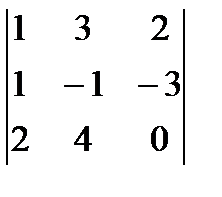 анық тауышынын мә ні: B)
анық тауышынын мә ні: B) 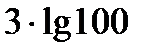
 анық тауышының мә ні: A) 11E)
анық тауышының мә ні: A) 11E) 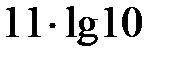
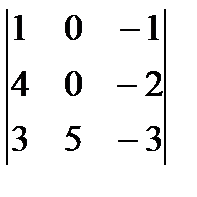 анық тауышының мә ні: B)
анық тауышының мә ні: B) 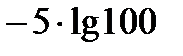
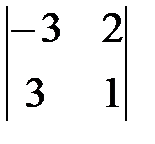 анық тауышының мә ні: B) -3 2 С)
анық тауышының мә ні: B) -3 2 С) 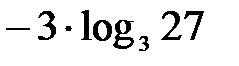
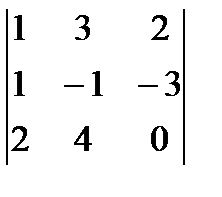 анық тауышының мә ні: C)
анық тауышының мә ні: C) 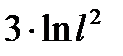 G)
G) 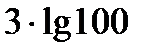
Функции и Тендеулер
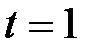 болғ анда
болғ анда 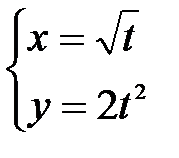 функциясының туындысы
функциясының туындысы 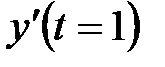 тең: A) 8 B)
тең: A) 8 B) 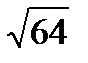 C)
C) 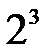
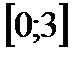 - де
- де 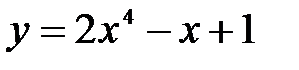 функциясының ең ү лкен мә нін табың дар: А) 160 В) 320/2
функциясының ең ү лкен мә нін табың дар: А) 160 В) 320/2
[0, 3]-де 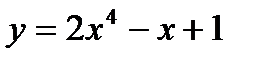 функциясының ен ү лкен мә ні C)
функциясының ен ү лкен мә ні C)  D)
D) 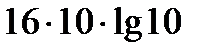 E)
E) 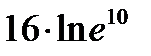
|
|
|
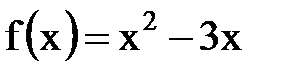 функциясы берілген.
функциясы берілген.  мә нін табың ыз: A)2/2 B)1
мә нін табың ыз: A)2/2 B)1
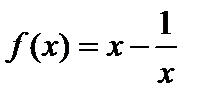 функциясының туындысы
функциясының туындысы 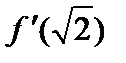 табың ыздар. A) 1, 5 B)15/10 C)3/2
табың ыздар. A) 1, 5 B)15/10 C)3/2
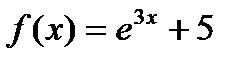 функциясының
функциясының 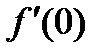 туындысының аралығ ы: A)[2; 4]
туындысының аралығ ы: A)[2; 4]
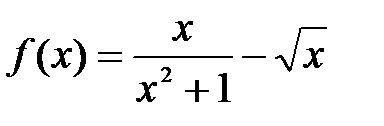 функциясының x=1 нү ктелеріндегі туындысын табың ыздар: A) -0, 5 B)-1/2
функциясының x=1 нү ктелеріндегі туындысын табың ыздар: A) -0, 5 B)-1/2
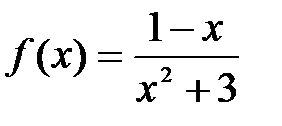 функциясының x=1 нү ктесіндегі туындысын табың ыздар: A) -0, 25 B)-1/4
функциясының x=1 нү ктесіндегі туындысын табың ыздар: A) -0, 25 B)-1/4
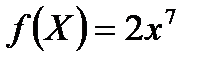 функциясының алғ ашқ ы функциясы А)
функциясының алғ ашқ ы функциясы А) 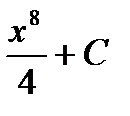 В)
В) 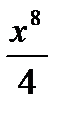 С)
С) 
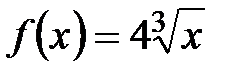 функциясының алғ ашқ ы функциясы А)
функциясының алғ ашқ ы функциясы А) 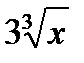
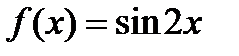 функциясының
функциясының 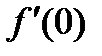 туындысы: А) 3-тен кіші В) 2-ге тең
туындысы: А) 3-тен кіші В) 2-ге тең
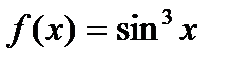 функциясының
функциясының 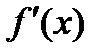 туындысы А)
туындысы А)  В)
В) 
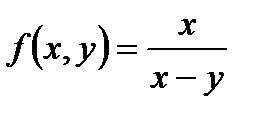 функциясы ү шін
функциясы ү шін 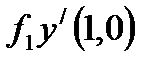 дербес туындысы: А) оң сан В) 1
дербес туындысы: А) оң сан В) 1
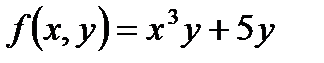 функциясы ү шін
функциясы ү шін 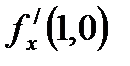 дербес туындысы А) 0 В) теріс емес сан
дербес туындысы А) 0 В) теріс емес сан
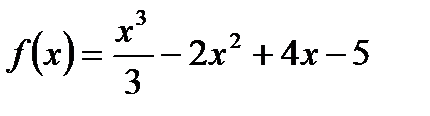 функциясының
функциясының 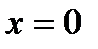 нү ктедегі 2-ші ретті туындысы: А) бү тін сан В) -4
нү ктедегі 2-ші ретті туындысы: А) бү тін сан В) -4
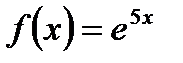 функциясының
функциясының 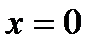 нү ктедегі 2-ші ретті туындысы: А) оң сан В) 25
нү ктедегі 2-ші ретті туындысы: А) оң сан В) 25
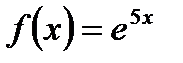 функциясының
функциясының 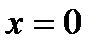 нү ктедегі екінші ретті туындысы. А) Оң сан. В) 25 С) Бү тін сан.
нү ктедегі екінші ретті туындысы. А) Оң сан. В) 25 С) Бү тін сан.
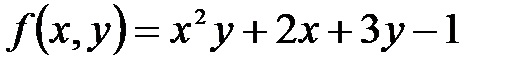 функциясы ү шін
функциясы ү шін 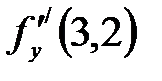 дербес туындысы: А) 12 В) Бү тін
дербес туындысы: А) 12 В) Бү тін 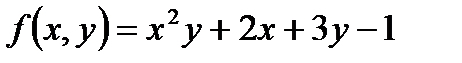 функциясы ү шін
функциясы ү шін 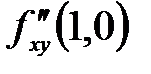 дербес туындысы: А) 2 В) Оң сан. C) нақ ты сан
дербес туындысы: А) 2 В) Оң сан. C) нақ ты сан
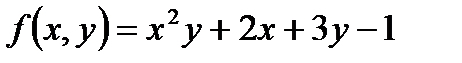 функциясы ү шін
функциясы ү шін 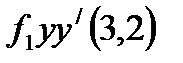 дербес туындысы: А) 6 В) бү тін сан
дербес туындысы: А) 6 В) бү тін сан
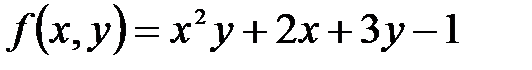 функциясы ү шін
функциясы ү шін 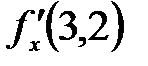 дербес туындысы: А) Оң сан. В) Бү тін сан. С) 18
дербес туындысы: А) Оң сан. В) Бү тін сан. С) 18
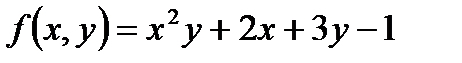 функциясы ү шін
функциясы ү шін 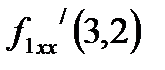 дербес туындысы: А) оң санВ) бү тін санС) 4
дербес туындысы: А) оң санВ) бү тін санС) 4
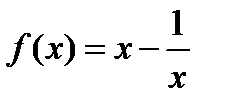 функциясының
функциясының 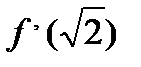 табың дар. C)1, 5
табың дар. C)1, 5
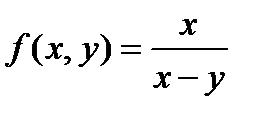 функциясы ү шін
функциясы ү шін 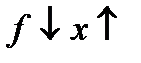 (1, 0) дербес туындысы: B)0 C)бү тін сан E)нақ ты сан
(1, 0) дербес туындысы: B)0 C)бү тін сан E)нақ ты сан
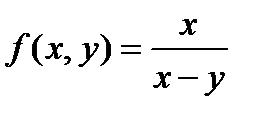 функциясы ү шін
функциясы ү шін 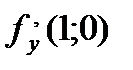 нү ктесіндегі дербес туындысының мә ні: A)
нү ктесіндегі дербес туындысының мә ні: A)  C)lg10 G)100
C)lg10 G)100
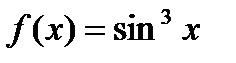 функциясының
функциясының  туындысы: B)
туындысы: B) 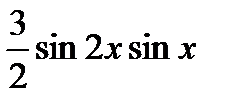 C)
C) 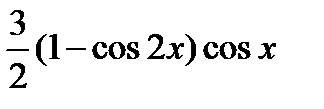 E)
E) 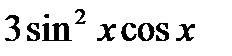
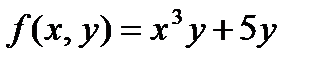 функциясы ү шін
функциясы ү шін 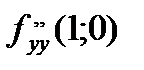 нү ктесіндегі дербес туындысының мә ні: D)
нү ктесіндегі дербес туындысының мә ні: D) 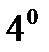 F)
F) 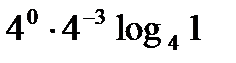
f(x)=e3x+5 функциясының f(0) туындысының мә ні жататын аралық: B)[1; 3] E)[3; 5]
f(x)=sin2x функциясының 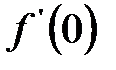 туындысы: C) 1-ден ү лкен E) 3-тен кіші G) 2ге тең
туындысы: C) 1-ден ү лкен E) 3-тен кіші G) 2ге тең
ƒ (x, y)=x2y+2x+3y-1 функциясы ү шін ƒ ¢ хх(3, 2) нү ктесіндегі дербес туындысының мә ні мына аралық тарда жатады: А)(0; 5), D)[4; 5), G) (3; 5)
f(x, y)=x2y+2x+3y-1функциясы ү шін(3; 2)нү ктесіндегі дербес туындысының мә ні: D) log24E)  F)18/2
F)18/2
|
|
|
F(1; 0)ү ктесінең жә не х=2тү зуінен бірдей аралық та орналасқ ан нү ктелердің геометриялық орының тең деуі A) 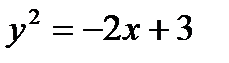
YYYYYYYYYYYY
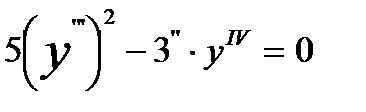 Дифференцифалдық тең деуінің реті тең: D)
Дифференцифалдық тең деуінің реті тең: D) 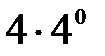 E)
E) 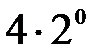 F)
F) 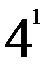
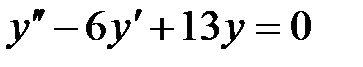 сызық тық біртекті дифференциалдық тең деуінің жалпы шешімін табың ыз. A)
сызық тық біртекті дифференциалдық тең деуінің жалпы шешімін табың ыз. A) 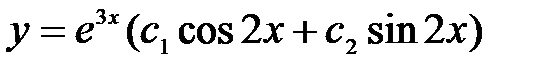 B)
B) 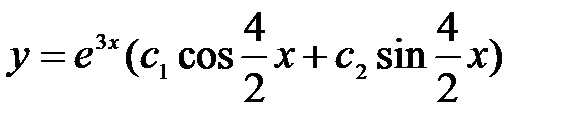
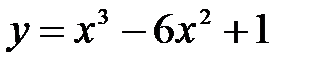 функциясының [-1; 2] кесіндісінің ең кіші мә нін табың ыздар. A) -15 B)-30/2
функциясының [-1; 2] кесіндісінің ең кіші мә нін табың ыздар. A) -15 B)-30/2
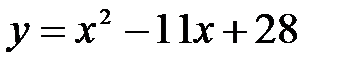 функциясының [4, 5] кесіндісінде ең ү лкен мә нін табың ыздар. A) 0
функциясының [4, 5] кесіндісінде ең ү лкен мә нін табың ыздар. A) 0
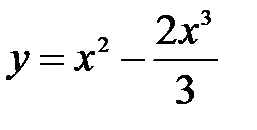 функциясының кему интервалын табың ыз: A)
функциясының кему интервалын табың ыз: A) 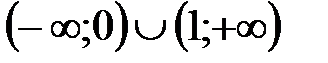 B)
B) 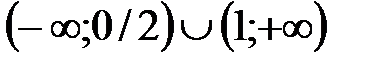
 функциясының минимумын табың ыз: A)-36 B)
функциясының минимумын табың ыз: A)-36 B) 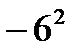
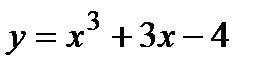 функциясының
функциясының 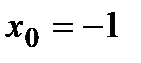 нү ктесіндегі туындысын табың ыздар. A) 6 B)18/3
нү ктесіндегі туындысын табың ыздар. A) 6 B)18/3
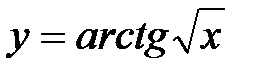 функциясының
функциясының 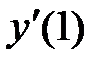 туындысын есептең із; A) 0, 25
туындысын есептең із; A) 0, 25
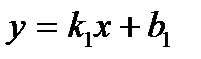 жә не
жә не 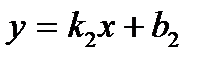 тү зулерінің арасындағ ы бұ рыш табу формуласын кө рсетің із: A)
тү зулерінің арасындағ ы бұ рыш табу формуласын кө рсетің із: A) 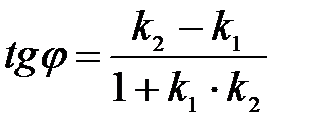
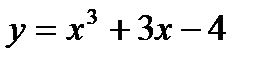 функциясының
функциясының 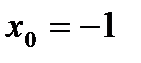 нү ктесіндегі туындысын табу керек А)12/2В)6 С) 0, 6*10
нү ктесіндегі туындысын табу керек А)12/2В)6 С) 0, 6*10
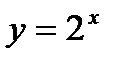 функциясының
функциясының 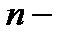 ші ретті туындысы: А)
ші ретті туындысы: А) 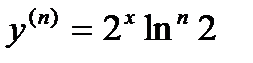
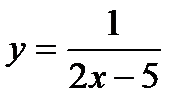 функцияның анық талу облысы: В)
функцияның анық талу облысы: В)  D)
D) 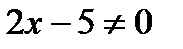
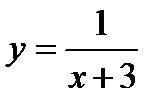 функциясы ү шін: C)
функциясы ү шін: C) 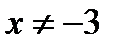 -анық талу облысы F) х=-3-ү зіліс нү ктесі
-анық талу облысы F) х=-3-ү зіліс нү ктесі
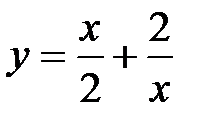 функциясының максимумын анық тау керек: B)-2C)-6/3E)-4/2
функциясының максимумын анық тау керек: B)-2C)-6/3E)-4/2
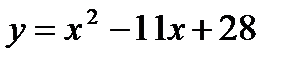 функциясының
функциясының 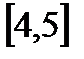 кесіндісінде ең ү лкен мә нін табың дар: E)0/7 F)0
кесіндісінде ең ү лкен мә нін табың дар: E)0/7 F)0
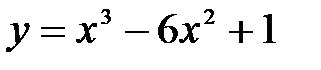 функциясының
функциясының 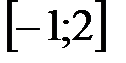 кесіндісіндегі ең кіші мә ні: C)
кесіндісіндегі ең кіші мә ні: C) 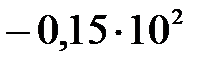 D)
D) 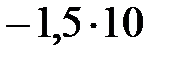 E)
E) 
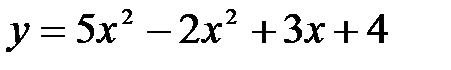 функциясының x=1 нү ктесіндегі туындысын табың дар: A)14 D)0, 14*102 E)
функциясының x=1 нү ктесіндегі туындысын табың дар: A)14 D)0, 14*102 E) 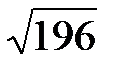
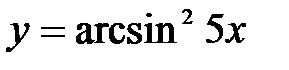 функциясының туындысы: A)
функциясының туындысы: A) 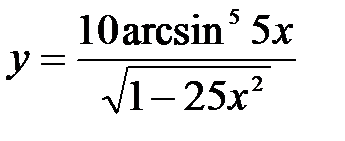 D)
D)  F)
F) 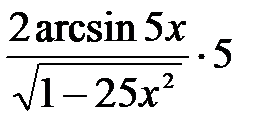
 функцияның кему аралығ ын табың ыз: A)
функцияның кему аралығ ын табың ыз: A) 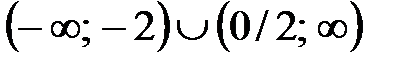 B)
B) 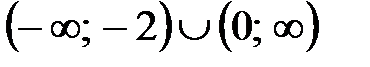
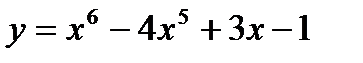 функцияның туындысы тең: D)
функцияның туындысы тең: D) 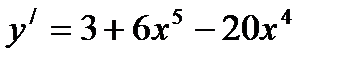 Е)
Е) 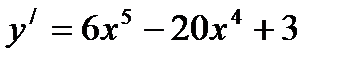
 функциясының ү шінші ретті дефференциалы
функциясының ү шінші ретті дефференциалы 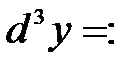 C)
C) 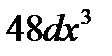 D)
D) 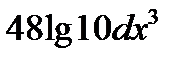 F)
F) 
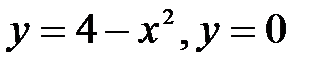 сызық тарымен шектелген фигураның ауданы: B)
сызық тарымен шектелген фигураның ауданы: B) 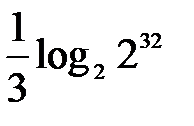 E)
E) 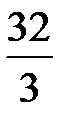
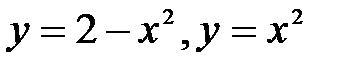 сызық тарымен шектелген фигураның ауданы: B)
сызық тарымен шектелген фигураның ауданы: B) 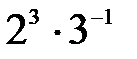 E)
E) 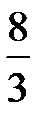
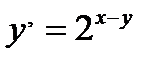 дифференциалдық тең деуінің жалпы шешімі: A)
дифференциалдық тең деуінің жалпы шешімі: A) 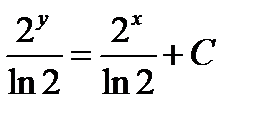 ; D)
; D) 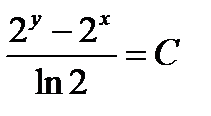
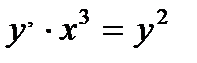 дифференциалдық тең деуінің реті: D) lne E) 20 G) log22
дифференциалдық тең деуінің реті: D) lne E) 20 G) log22
y=2x-3жә неy=2x+10 тү зулері: E)0  Бұ рыш жасайдыF)Бірдей бұ рыштық коэффицентке ие G)параллель
Бұ рыш жасайдыF)Бірдей бұ рыштық коэффицентке ие G)параллель
y=-3 тү зуі: B)Oy ө сінен -3-ке тең кесінді қ ияды: C)Ox ө сіне параллель G)(0; -3) нү ктесі арқ ылы ө теді
y=5x+7 жә не 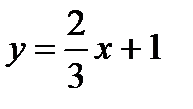 тү зулерінің арасындағ ы бұ рыштың аралығ ы: D)
тү зулерінің арасындағ ы бұ рыштың аралығ ы: D) 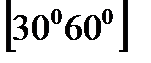
y=cos3x функциясының ү шінші ретт 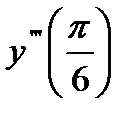 туындысы: B) 27-ге тең: E) 26-дан ү лкен
туындысы: B) 27-ге тең: E) 26-дан ү лкен
|
|
|
y=xтү зуі: A) (0; 0)нү ктесі арқ ылы ө теді D)0xө сімен 135 бұ рыш жасайды
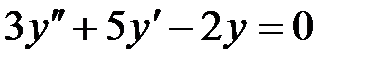 тендеуінің жалпы шешімін табың ыз. A)
тендеуінің жалпы шешімін табың ыз. A) 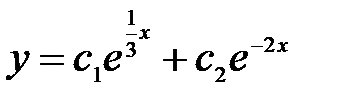 B)
B) 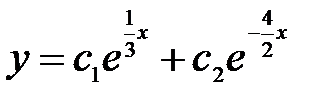
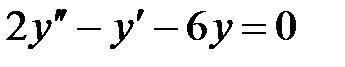 тең деуінің жалпы шешімін табың ыз: A)
тең деуінің жалпы шешімін табың ыз: A) 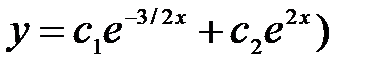
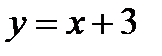 тү зуі А) Ох ө сімен 450 бұ рыш жасайды В) Оу ө сінен 3-ке тең кесінді қ ияды C)
тү зуі А) Ох ө сімен 450 бұ рыш жасайды В) Оу ө сінен 3-ке тең кесінді қ ияды C) 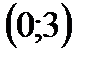 нү ктесі арқ ылы ө теді
нү ктесі арқ ылы ө теді
 функциясының максимумын анық тау керек. A) -2 B)-6/3
функциясының максимумын анық тау керек. A) -2 B)-6/3
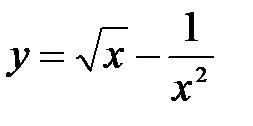 функциясының
функциясының 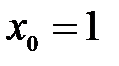 нү ктесіндегі туындысын табың ыздар. A) 2, 5 B)25/10 C)5/2
нү ктесіндегі туындысын табың ыздар. A) 2, 5 B)25/10 C)5/2
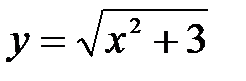 функциясының x=1 нү ктесіндегі туындысын табың ыздар.
функциясының x=1 нү ктесіндегі туындысын табың ыздар. 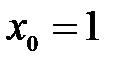 : A) 0, 5 B)1/2 C)2/4
: A) 0, 5 B)1/2 C)2/4
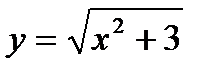 функциясының туындысының
функциясының туындысының 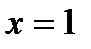 нү ктесіндегі мә нін табың дар: А) 2/4
нү ктесіндегі мә нін табың дар: А) 2/4
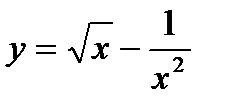 функциясының туындысының
функциясының туындысының 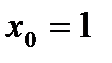 нү ктесіндегі мә нін табың дар: А) 25/10 В) 5/2 С) 2, 5
нү ктесіндегі мә нін табың дар: А) 25/10 В) 5/2 С) 2, 5
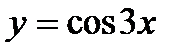 функциясының ү шінші ретті
функциясының ү шінші ретті 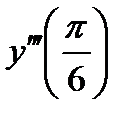 туындысы А) 28-ден кіші
туындысы А) 28-ден кіші
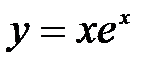 функциясының х=0 нү ктесіндегі екінші ретті туындысын табың ыз; A) 2
функциясының х=0 нү ктесіндегі екінші ретті туындысын табың ыз; A) 2
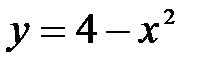 параболасымен шектелген фигураның ауданын есептең із: A)
параболасымен шектелген фигураның ауданын есептең із: A) 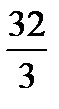 B)
B) 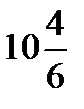 C)
C) 
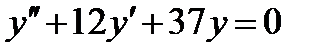 сызық тық біртекті дифференциалдық тең деуінің жалпы шешімін табың ыз: A)
сызық тық біртекті дифференциалдық тең деуінің жалпы шешімін табың ыз: A) 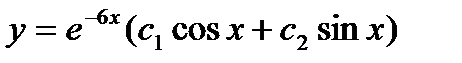 B)
B) 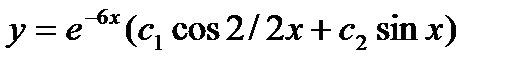 C)
C) 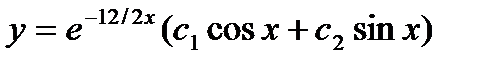
 тең деуіне сә йкес біртекті сызық ты тең деуінің жалпы шешімін кө сетің із: A)
тең деуіне сә йкес біртекті сызық ты тең деуінің жалпы шешімін кө сетің із: A) 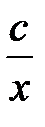 B)
B) 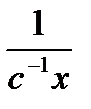 C)
C) 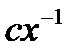
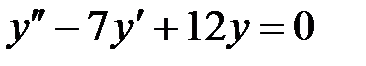 тең деуінің жалпы шешімін табың ыз: A)
тең деуінің жалпы шешімін табың ыз: A) 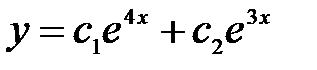 B)
B) 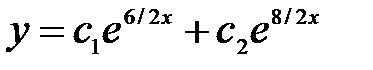 C)
C) 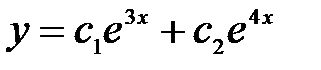
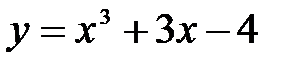 функциясының
функциясының 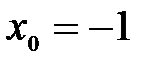 нү ктесіндегі туындысын табың ыздар. A) 12/2 B)18/3 C)6
нү ктесіндегі туындысын табың ыздар. A) 12/2 B)18/3 C)6
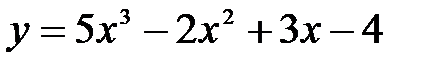 функциясының
функциясының 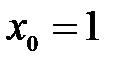 нү ктесіндегі туындысын табың ыздар. A) 14 B)42/3 C)28/2
нү ктесіндегі туындысын табың ыздар. A) 14 B)42/3 C)28/2
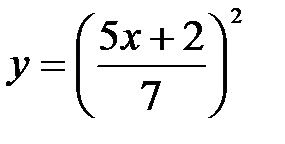 функциясының
функциясының 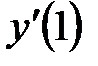 туындысы. A)10/7 B20/14 C)30/21
туындысы. A)10/7 B20/14 C)30/21
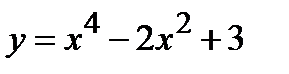 функциясының [-2; 2] кесіндісіндегі ең ү лкен мә нін табың ыздар: A) 11 B)99/9
функциясының [-2; 2] кесіндісіндегі ең ү лкен мә нін табың ыздар: A) 11 B)99/9
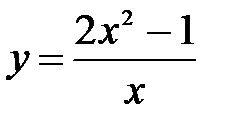 функциясының кө лбеу асимптотасын табың ыз: A)
функциясының кө лбеу асимптотасын табың ыз: A) 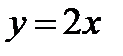 B)
B) 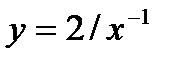 C)
C) 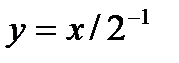
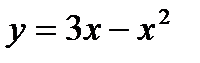 жә не
жә не 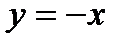 сызық тармен шектелген фигураның ауданы: А)
сызық тармен шектелген фигураның ауданы: А) 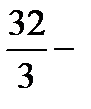 ке тең
ке тең
 тү зуі: А) Ох ө сімен 1350 бұ рыш жасайды В)
тү зуі: А) Ох ө сімен 1350 бұ рыш жасайды В) 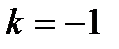 бұ рыштық коэффициентке ие
бұ рыштық коэффициентке ие
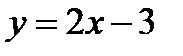 жә не
жә не 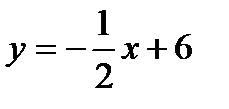 тү зулері: А) Перпендикуляр. В) 900 бұ рыш жасайды.
тү зулері: А) Перпендикуляр. В) 900 бұ рыш жасайды.
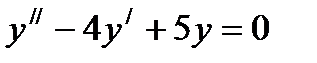 дифференциалдық тең деудің жалпы шешімі мынадай: А)
дифференциалдық тең деудің жалпы шешімі мынадай: А) 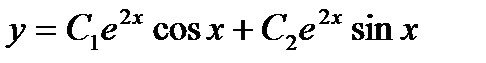 D)
D) 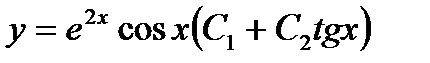
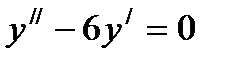 дифференциалдық тең деудің жалпы шешімі мынадай: А)
дифференциалдық тең деудің жалпы шешімі мынадай: А) 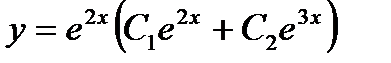 D)
D) 
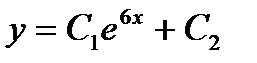
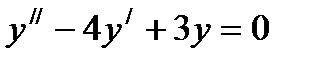 дифференциалдық тең деудің жалпы шешімі мынадай: А)
дифференциалдық тең деудің жалпы шешімі мынадай: А) 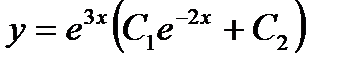 D)
D) 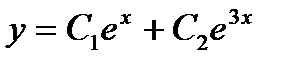
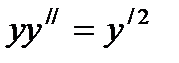 дифференциалдық тең деудің жалпы шешімі мынадай: С)
дифференциалдық тең деудің жалпы шешімі мынадай: С) 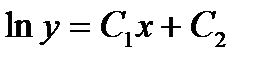 D)
D) 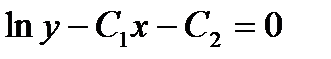
|
|
|
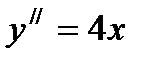 дифференциалдық тең деудің жалпы шешімі мынадай: Шешімі жоқ
дифференциалдық тең деудің жалпы шешімі мынадай: Шешімі жоқ
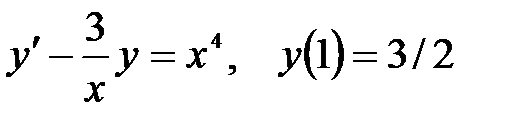 Коши есебін шешің із: A)
Коши есебін шешің із: A) 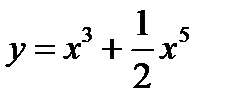 B)
B) 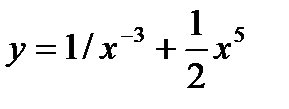 C)
C) 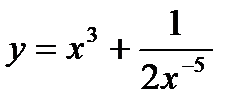
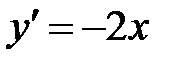 дифференциалдық тең деуін шешің із: A)
дифференциалдық тең деуін шешің із: A) 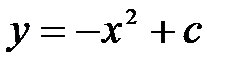
 дифференциалдық тең деуінің реті тең: A) 1B)
дифференциалдық тең деуінің реті тең: A) 1B) 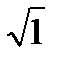
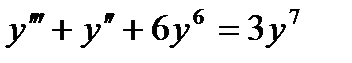 дифференциалдық тең деуінің реті тең: A) 3
дифференциалдық тең деуінің реті тең: A) 3
 дифференциалдық тең деуінің шешімін табың ыз. A)
дифференциалдық тең деуінің шешімін табың ыз. A) 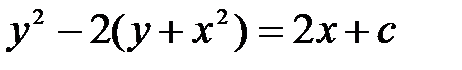 B)
B) 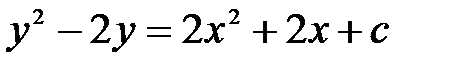
 дифференциалдық тең деуінің шешімін табың ыз. A)
дифференциалдық тең деуінің шешімін табың ыз. A) 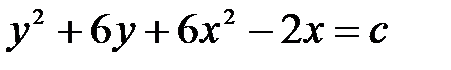 B)
B) 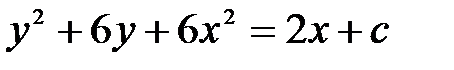
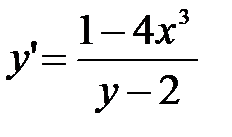 дифференциалдық тең деуінің шешімін табың ыз: A)
дифференциалдық тең деуінің шешімін табың ыз: A) 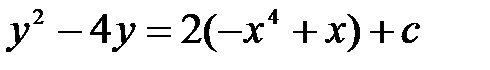 B)
B) 
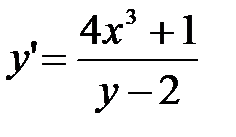 дифференциалдық тең деуінің шешімін табың ыз: A)
дифференциалдық тең деуінің шешімін табың ыз: A) 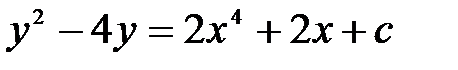 B)
B) 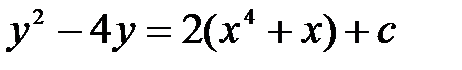
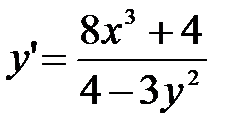 дифференциалдық тең деуінің шешімін табың ыз: A)
дифференциалдық тең деуінің шешімін табың ыз: A)  B)
B) 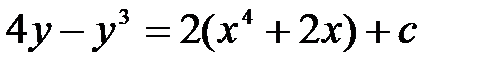
|
|
|


