 |
Ввввггггдддд. Ееееееееее
|
|
|
|
ВВВВГГГГДДДД
Векторларғ а сызық тық амалдар қ олдану кезінде орындалатын қ асиеттер: А)  мұ ндағ ы
мұ ндағ ы 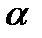 жә не
жә не 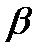 тұ рақ тылар В)
тұ рақ тылар В) 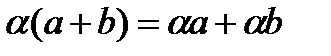 С)
С) 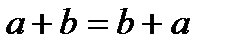
Векторлардың компланарлық шарты: А) осы векторлардан қ ұ рылғ ан параллелипедтің кө лемі кез-келген оң санғ а тең
Векторлық кө бейтіндінің қ асиеттері: А) 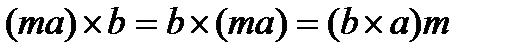 В)
В) 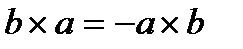 С)
С) 
Векторлардын компланарлық шарты: C)Аралас кө бейтіндісі нө лге тең F)Осы векторлардан қ ұ ралғ ан параллелепипедтін кө лемі нө лге тең
Гармоникалық қ атардың тү рі: A) 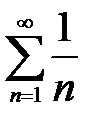
Даламбер белгісі бойынша қ атар  : D)жинақ ты, ө йткені g< 1
: D)жинақ ты, ө йткені g< 1
Даламбер белгісі бойынша қ атар  А) жинақ ты, ө йткені
А) жинақ ты, ө йткені  В) жинақ ты
В) жинақ ты
Даламбер белгісі бойынша қ атар 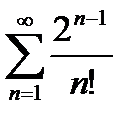 А) жинақ ты В) жинақ ты, ө йткені
А) жинақ ты В) жинақ ты, ө йткені 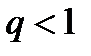
Дә режелік қ атардың  жалпы мү шесі келесі ө рнек болады: A)
жалпы мү шесі келесі ө рнек болады: A) 
Дә режелік қ атардың 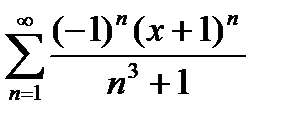 жалпы мү шесінің коэффициенті тең. A)
жалпы мү шесінің коэффициенті тең. A)  B)
B)  C)
C) 
Дә режелік қ атардың  жалпы мү шесі келесі функция болады: A)
жалпы мү шесі келесі функция болады: A) 
Дисперсия 1/36 - ке тең болса, онда орташа квадраттық ауытқ уды табың ыз. A) 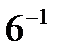 B)1/6 C) 1/
B)1/6 C) 1/ 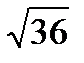
ЕЕЕЕЕЕЕЕЕЕ
Егер  функциясы біртекті болса, онда оның біртектілік дә режесі: D)
функциясы біртекті болса, онда оның біртектілік дә режесі: D)  F)ln1 H)
F)ln1 H) 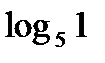
Егер f(x, y)= 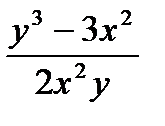 функциясы бір текті болса онда оның біртектілік дә режесі: A) log31
функциясы бір текті болса онда оның біртектілік дә режесі: A) log31
Егер y(x)= 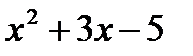 болса, онда
болса, онда  : B)
: B)  E)
E) 
Егерf(x)=  болсаf(0)табу керек: A)0/9 E)1n1F)0
болсаf(0)табу керек: A)0/9 E)1n1F)0
Егерf(x)=3x-2 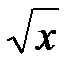 болсаf(1)табу керек: C)6/3 D)2 E)4/2
болсаf(1)табу керек: C)6/3 D)2 E)4/2
Екі вектордан векторлық кө бейтіндісінің модулі: B)Осы векторлардан қ ұ ралғ ан параллелограммның ауданың а тең
Екінші ретті дифференциалдық тең деу: C)  D)
D) 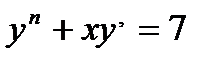 E)
E) 
Екінші ретті сызық тық дифференциалдық тең деудің  сипаттаушы тең деуінің тү бірлері: B)
сипаттаушы тең деуінің тү бірлері: B) 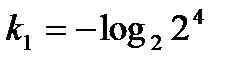 ,
, 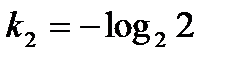 E)
E) 
|
|
|
Екінші ретті сызық тық дифференциалдық тең деудің 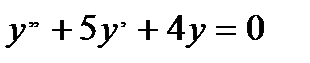 сипаттаушы тең деуінің тү бірлері: A)
сипаттаушы тең деуінің тү бірлері: A)  ,
,  C)
C) 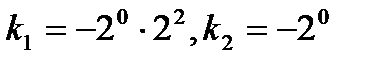 F)
F) 
Есепте 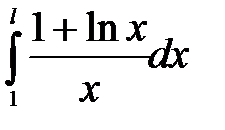 : B)15/10
: B)15/10
Есепте:  A)20/2
A)20/2
Есепте: 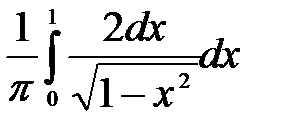 A)2/2
A)2/2
Есепте:  : A)4, 5E)9/2F)45/10
: A)4, 5E)9/2F)45/10
Есепте: 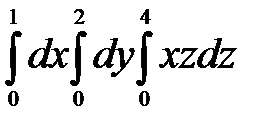 : A)16/2 C)8 B)
: A)16/2 C)8 B) 
Егер  болса,
болса,  табу керек: A) 3
табу керек: A) 3
Егер 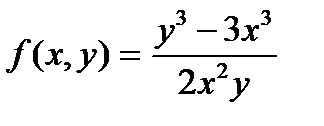 функциясы біртекті болса, онда оның біртектілік дә режесін табу керек: А)324.
функциясы біртекті болса, онда оның біртектілік дә режесін табу керек: А)324.
Егер 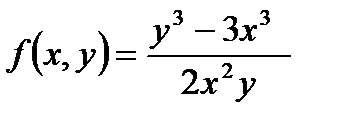 функциясы біртекті болса, онда оның біртектілік дә режесін табу керек: А) 0 В)
функциясы біртекті болса, онда оның біртектілік дә режесін табу керек: А) 0 В) 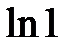
Егер  ,
,  болса,
болса,  векторының координаттары тең: Д)
векторының координаттары тең: Д)  Е)
Е) 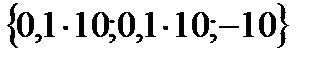
Егер  болса,
болса, 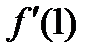 табу керек:
табу керек:  A)2
A)2
Егер 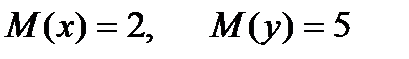 берілген болса, онда
берілген болса, онда  кездейсоқ шаманың математикалық ү мітін табың ыз A)
кездейсоқ шаманың математикалық ү мітін табың ыз A)  B)3 C)
B)3 C) 
Егер  берілген болса, онда
берілген болса, онда  кездейсоқ шаманың математикалық ү мітін табың ыз. A)-4 B)-12/3 C)-8/2
кездейсоқ шаманың математикалық ү мітін табың ыз. A)-4 B)-12/3 C)-8/2
Егер 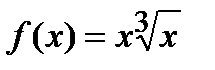 болса,
болса, 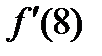 табу керек: A)8/3
табу керек: A)8/3
Егер  болса,
болса, 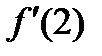 табу керек: A)2/9
табу керек: A)2/9
Егер  болса, у¢ (1) табу керек: A)5
болса, у¢ (1) табу керек: A)5
Егер 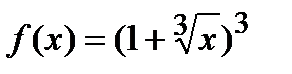 болса,
болса,  табу керек: A) 4
табу керек: A) 4
Егер f(x) =  болса,
болса, 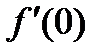 табу керек: A) 0
табу керек: A) 0
Екі белгісізі бар сызық тық тең деуді шешің із.  : А) (2, -2)
: А) (2, -2)
Екінші ретті анық тауышты есептең із:  тең: A)
тең: A) 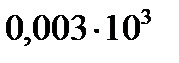
Екінші ретті сызық тық дифференциалдық тең деудің  сипаттаушы тең деуінің тү бірлері: А) екі тү бірі де теріс сан В)
сипаттаушы тең деуінің тү бірлері: А) екі тү бірі де теріс сан В) 
Емтихан кезінде студент жоспар бойынша қ ойылатын 50 сұ рақ тың 30-на дайындалғ ан. Емтиханда берілген 3 сұ рақ тың екеуіне жауап беру ық тималдығ ы тең: А) 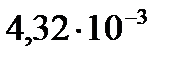 В)
В) 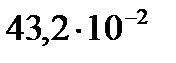 D)
D) 
Есепте  А) 0, 1*10
А) 0, 1*10
Есепте 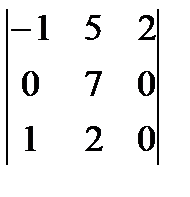 А) -14В) -28/2С) -42/3
А) -14В) -28/2С) -42/3
Есепте  А) 1В) 2/2С) 8/8
А) 1В) 2/2С) 8/8
Есепте 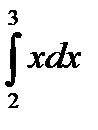 А) 2, 5В) 5/2
А) 2, 5В) 5/2
Есепте  А) 45/3В) 15
А) 45/3В) 15
Есепте  А) 6
А) 6 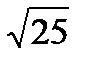 В)
В) 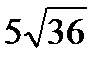 С) 30
С) 30
Есепте.  А) 0, 1*10
А) 0, 1*10
Есепте:  А) 24/3
А) 24/3
Есепте:  А) 30/8 В) 15/4 С) 45/12
А) 30/8 В) 15/4 С) 45/12
Есепте:  А) 8 В) 24/3 С) 16/2
А) 8 В) 24/3 С) 16/2
Есепте:  А)
А)  В) 4С)
В) 4С) 
Есепте:  А)
А)  В)
В) 
Есепте: 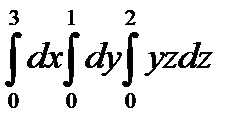 А)
А) 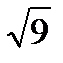 В)
В) 
Есептең із. 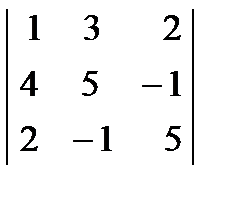 A) -70
A) -70
Есептең із.  A) 2
A) 2
Есептең із.  A)6 B) 24/4 C)36/6
A)6 B) 24/4 C)36/6
Есептең із. 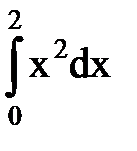 A)8/3 B)
A)8/3 B) 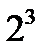 /3
/3
Есептең із. 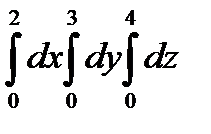 A) 72/3 B)24 C)48/2
A) 72/3 B)24 C)48/2
Есептең із..  А) -12В) -48/4 С) -24/2
А) -12В) -48/4 С) -24/2
|
|
|
Есептең із.  А) -14 В) -28/2С) -42/3
А) -14 В) -28/2С) -42/3
Есептең із..  А) 20/2 В)30/3 С)40/4
А) 20/2 В)30/3 С)40/4
Есептең із. 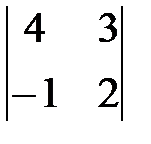 А) 22/2 В) 33/3 С) 11
А) 22/2 В) 33/3 С) 11
Есептең із.  А) 24/2 В) 48/4 С)12
А) 24/2 В) 48/4 С)12
Есептең із..  . A) ½ B)
. A) ½ B) 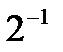
Есептең із.  . A)
. A) 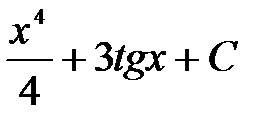 B)
B) 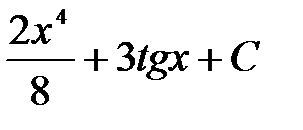
Есептең із. 
 A)
A) 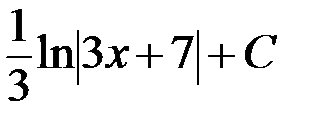 B)
B) 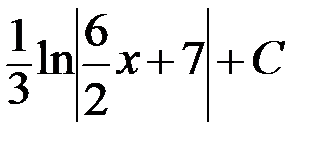
Есептең із..  . A)
. A)  B)
B) 
Есептең із..  A) 1 B)3/3
A) 1 B)3/3
Есептең із. .  A) 12, 8 B)128/10
A) 12, 8 B)128/10
Есептең із.. 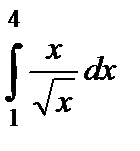 A) 14/3 B)28/6
A) 14/3 B)28/6
Есептең із..  A) 16 B)32/2
A) 16 B)32/2
Есептең із.  A) 2, 5 B)5/2
A) 2, 5 B)5/2
Есептең із.. 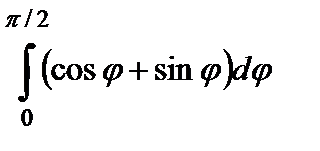 A) 2 B)4/2
A) 2 B)4/2
Есептең із..  A) 3/8 B)6/16
A) 3/8 B)6/16
Есептең із.  A) 4, 5 B)9/2
A) 4, 5 B)9/2
Есептең із..  A) 66 B)198/3
A) 66 B)198/3
Есептең із.. 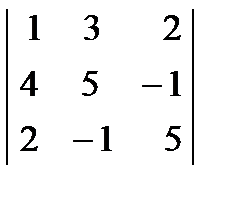 A) -70 B)-140/2
A) -70 B)-140/2
Есептең із..  A) 8/3 B)16/6
A) 8/3 B)16/6
Есептең із..  A) 8/9 B)24/27
A) 8/9 B)24/27
Есептең із.  A)p/3 B) 2p/6
A)p/3 B) 2p/6
Есептең із.  A)
A) 
Есептең із.  A)
A)  B)
B) 
Есептең із. 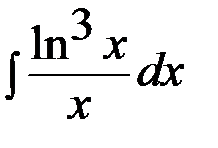 A)
A)  B)
B) 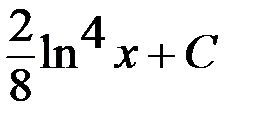
Есептең із. . 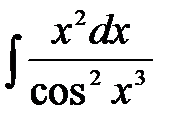 A)
A) 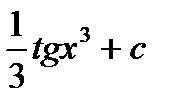 B)
B) 
Есептең із. . 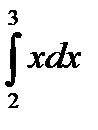 А) 2, 5 В) 5/2
А) 2, 5 В) 5/2
Есептең із. .  А) 45/3 В) 15
А) 45/3 В) 15
Есептең із. .  А) 88/2 В) 44
А) 88/2 В) 44
Есептең із. . 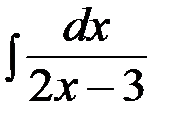 А)
А)  В)
В) 
Есептең із. : 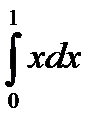 A) 0, 5
A) 0, 5
Есептең із. : 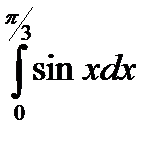 A) 0, 5
A) 0, 5
Есептең із. : 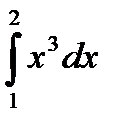 A) 15/4
A) 15/4
Есептең із. :  A) 16
A) 16
Есептең із. : 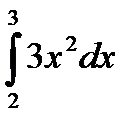 A) 19
A) 19
Есептең із. :  A) 2
A) 2
Есептең із. :  A) 2, 5
A) 2, 5
Есептең із. :  A) 6/3 B)2
A) 6/3 B)2
Есептең із. :  A) 66 B)132/2
A) 66 B)132/2
Есептең із. :  A) 8/3
A) 8/3
Есептең із. :  A) 8/9 B)24/27
A) 8/9 B)24/27
Есептең із. : 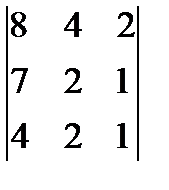 A) 0
A) 0
Есептең із. :  A) 0
A) 0
Есептең із. :  A) 1
A) 1
Есептең із. :  A) –10
A) –10
Есептең із. : 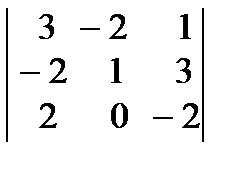 A) –12
A) –12
Есептең із. :  A) –14
A) –14
Есептең із. :  A) 24
A) 24
Есептең із. : 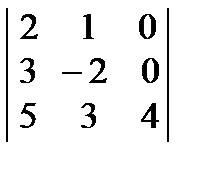 A) –28
A) –28
Есептең із. : 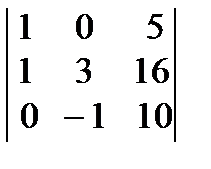 A) 41
A) 41
Есептең із. : 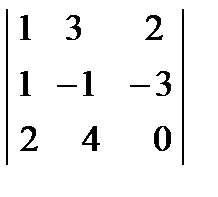 A) 6
A) 6
Есептең із. : 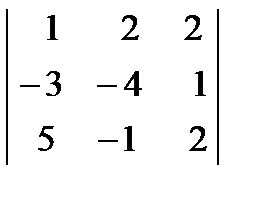 A) 61
A) 61
Есептең із. :  A) 8
A) 8
Есептең із. : 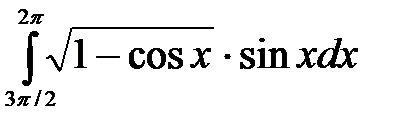 A) -2/3
A) -2/3
Есептең із. :  A) 8/9
A) 8/9
Есептең із.  А) 1
А) 1
Есептең із.. 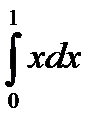 A) 0, 5 B)1/2
A) 0, 5 B)1/2
Есептең із.: 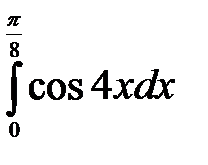 . A) 1/4
. A) 1/4
Есептең із.:  . A) 1/5
. A) 1/5
Есептең із. 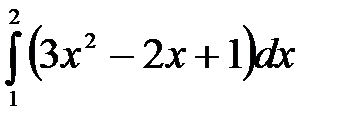 А) 5 В) Бү тін сан.
А) 5 В) Бү тін сан.
|
|
|


