 |
Интеграл, Дифференциал и сумма
|
|
|
|
Интеграл, Дифференциал и сумма
 интегралы: А)
интегралы: А)  Е)
Е) 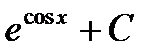
 анық талғ ан интеграл: А) 0, 25 D) 2/8 Е) ¼
анық талғ ан интеграл: А) 0, 25 D) 2/8 Е) ¼
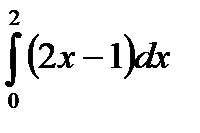 анық талмағ ан интегралдың мә ні тең: А)
анық талмағ ан интегралдың мә ні тең: А)  С)
С)  D)
D) 
 интегралы: А)
интегралы: А) 
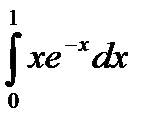 интегралы А)
интегралы А) 
 интегралы А)
интегралы А) 
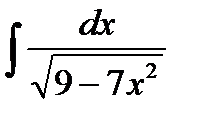 интегралы А)
интегралы А)  В)
В) 
 А) 1
А) 1
 А) 1/15 В) рационал санС) оң сан
А) 1/15 В) рационал санС) оң сан
 А) оң санВ)4С) бү тін сан
А) оң санВ)4С) бү тін сан
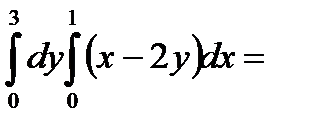 А) теріс санВ) рационал санС) 1
А) теріс санВ) рационал санС) 1
 интегралы: А)
интегралы: А) 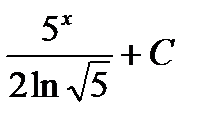
 интегралы А)
интегралы А)  тен кіші В)
тен кіші В)  ге тең
ге тең
 интегралы мә ні: D)0, 16
интегралы мә ні: D)0, 16  102
102
 интегралының мә ні: D)
интегралының мә ні: D)  E)
E) 
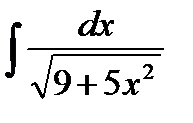 интегралы: A)
интегралы: A)  B)
B) 
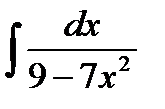 интегралы: C)
интегралы: C)  E)
E) 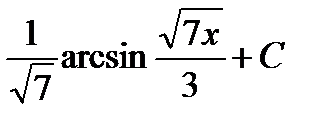
 интегралы: C)
интегралы: C)  E)
E) 
 интегралы: C)
интегралы: C) 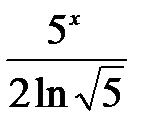 +CD)
+CD) 
 интегралы: D)
интегралы: D)  F)
F) 
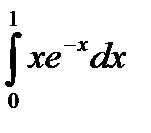 интегралы: D)
интегралы: D) 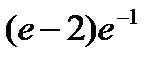 F)
F) 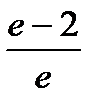
 интегралы: D)
интегралы: D)  Е)
Е) 
 интегралының мә ні B)
интегралының мә ні B) 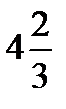 D)
D) 
 дә режелік қ атарының жинақ тылық радиусын табың ыз: A)
дә режелік қ атарының жинақ тылық радиусын табың ыз: A)  B)
B)  C)1/5
C)1/5
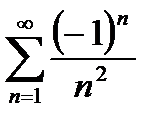 сандық қ атарының мү шелері: А)
сандық қ атарының мү шелері: А) 
 сандық қ атарының мү шелері А)
сандық қ атарының мү шелері А) 
 қ атарларының қ айсысы жинақ ты қ атар болады: A) 2
қ атарларының қ айсысы жинақ ты қ атар болады: A) 2
 қ атарының бесінші мү шесі А) оң сан В)
қ атарының бесінші мү шесі А) оң сан В) 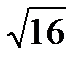 С) 4 (Рационал сан)
С) 4 (Рационал сан)
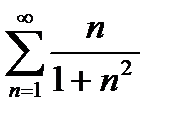 қ атарының тоғ ызыншы мү шесі А) рационал сан В) оң сан С) 9/82
қ атарының тоғ ызыншы мү шесі А) рационал сан В) оң сан С) 9/82
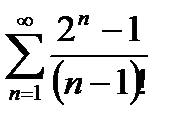 сандық қ атарының мү шелері: А)
сандық қ атарының мү шелері: А) 
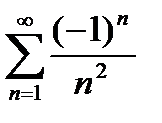 сандық қ атарының мү шелері А)
сандық қ атарының мү шелері А) 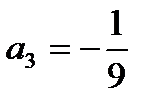 В)
В) 
 дә режелік қ атардың бесінші мү шесі тең: А)
дә режелік қ атардың бесінші мү шесі тең: А)  D)
D)  Е)
Е) 
 дә режелік қ атардың жинақ талу интервалы неге тең: В)
дә режелік қ атардың жинақ талу интервалы неге тең: В)  С)
С)  Е)
Е) 
 дә режелік қ атардың жинақ талу интервалы неге тең: А)
дә режелік қ атардың жинақ талу интервалы неге тең: А)  В)
В) 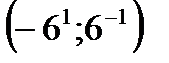 С)
С) 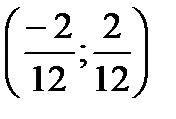
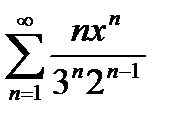 дә режелік қ атардың жинақ талу интервалы неге тең: В)
дә режелік қ атардың жинақ талу интервалы неге тең: В)  С)
С) 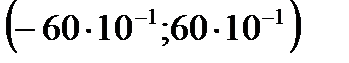 Е)
Е) 
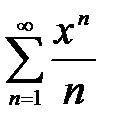 дә режелік қ атарының жинақ тылық радиусы тең: A) 1
дә режелік қ атарының жинақ тылық радиусы тең: A) 1
 қ атары кошидің радикалдық белгісі бойынша: D )жинақ сыз E) жинақ сыз, ө йткені q=e G) жинақ сыз, ө йткені q> 1
қ атары кошидің радикалдық белгісі бойынша: D )жинақ сыз E) жинақ сыз, ө йткені q=e G) жинақ сыз, ө йткені q> 1
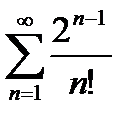 Қ атары Даламбер белгісі бойынша: B) жинақ ты D) жинақ ты, ө йткені q=0 F) жинақ ты, ө йткені
Қ атары Даламбер белгісі бойынша: B) жинақ ты D) жинақ ты, ө йткені q=0 F) жинақ ты, ө йткені 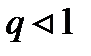

|
|
|
 қ атары Кошидің радикалдық белгісі бойынша: B) жинақ сыз, ө йткені
қ атары Кошидің радикалдық белгісі бойынша: B) жинақ сыз, ө йткені  C)жинақ сыз, ө йткені
C)жинақ сыз, ө йткені 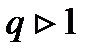
 қ атарының бесінші мү шесі: B)
қ атарының бесінші мү шесі: B)  C)4 F)оң сан
C)4 F)оң сан
 қ атарының тоғ ызыншы мү шесі: A)
қ атарының тоғ ызыншы мү шесі: A) 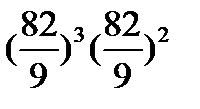 B)
B)  E)
E) 
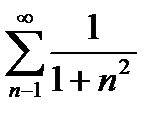 қ атарының тоғ ызыншы мү шесі: C)рационал сан
қ атарының тоғ ызыншы мү шесі: C)рационал сан
 сандық қ атарының мү шеслері: C)
сандық қ атарының мү шеслері: C)  E)
E)  F)
F) 
 сызық тық тең деуінің
сызық тық тең деуінің  -ін есепте: А) -25
-ін есепте: А) -25
 сызық тық тең деуінің
сызық тық тең деуінің 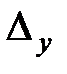 -ін есепте: А)-75 В)-150/2
-ін есепте: А)-75 В)-150/2
 жү йенің шешімдерінің қ осындысы мына аралық та жатады: C)[1; 3] E)[3; 5] F)[2; 4]
жү йенің шешімдерінің қ осындысы мына аралық та жатады: C)[1; 3] E)[3; 5] F)[2; 4]
 параметрлік функциясының yx туындысы: A)
параметрлік функциясының yx туындысы: A)  D)
D)  E)
E) 
 тең деуінің шешімі: A)x=-t, y=-t, z=t
тең деуінің шешімі: A)x=-t, y=-t, z=t
 тең деуінің шешімі: B)x=2t, y=t, z=-4t D)x+y+z=-t
тең деуінің шешімі: B)x=2t, y=t, z=-4t D)x+y+z=-t
 шешімдерінің қ осындысы мына аралық та жатады: A)[2; 4] B)[3; 5]
шешімдерінің қ осындысы мына аралық та жатады: A)[2; 4] B)[3; 5]
ШЕК
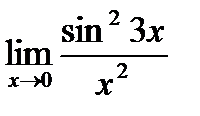 шегі: А) 9-ғ а тең В)10-нан кіші С)8-ден ү лкен
шегі: А) 9-ғ а тең В)10-нан кіші С)8-ден ү лкен
 шегі А) 1-ден кіші В)
шегі А) 1-ден кіші В)  нен кіші
нен кіші
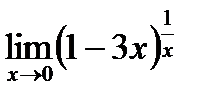 шегі А)0-ден ү лкен В)
шегі А)0-ден ү лкен В) 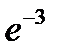 тең
тең
 А)
А) 
 функциясының шегі: С)
функциясының шегі: С)  D)
D) 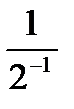
 шегі: А) 8-ден ү лкен В) 10-нан кіші
шегі: А) 8-ден ү лкен В) 10-нан кіші
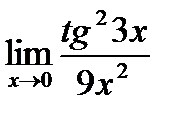 шегінің аралық та: А)[1; 3] B)[-1; 1]
шегінің аралық та: А)[1; 3] B)[-1; 1]
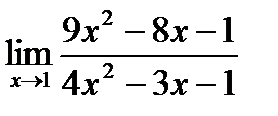 шегінің аралығ ы: А) [0; 2, 5]B)[2; 4]
шегінің аралығ ы: А) [0; 2, 5]B)[2; 4]
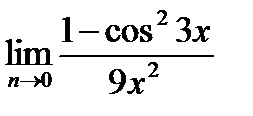 шегі: A)0-ден ү лкенB) 1-ге тең
шегі: A)0-ден ү лкенB) 1-ге тең
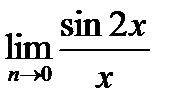 шегі: A)3-тен кішіD)2-ге тең E)
шегі: A)3-тен кішіD)2-ге тең E)  1-ден ү лкен
1-ден ү лкен
 шегі: A)log42
шегі: A)log42
 шегі: B)log42 C) 1-ден кіші
шегі: B)log42 C) 1-ден кіші
 шегінің мә ні: A)
шегінің мә ні: A) 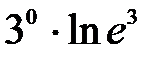 F)
F)  G)
G) 
 шегінің мә ні: C)
шегінің мә ні: C)  E)
E) 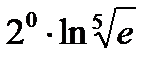 G)
G) 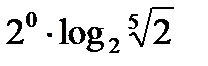
 шегі: A)1-ден кішіC)0-ден ү лкенE)0, 5-ке тең
шегі: A)1-ден кішіC)0-ден ү лкенE)0, 5-ке тең
 А)Нақ ты сан C)оң санF)
А)Нақ ты сан C)оң санF) 
ААААААА
 жә не
жә не 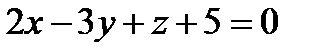 жазық тық тары А, В, С-ның сә йкес паралель мә ндері: А)
жазық тық тары А, В, С-ның сә йкес паралель мә ндері: А)
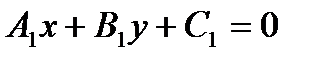 жә не
жә не  тү зулерінің паралльлелдік шартын кө рсетің із: A)
тү зулерінің паралльлелдік шартын кө рсетің із: A) 
-2, 3, -1 В) 4, -6, 2 С) -6, 9, -3
 жә не
жә не  нү ктелері берілген.
нү ктелері берілген. 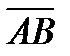 кесіндісінің ортасының ординатасы А) 0
кесіндісінің ортасының ординатасы А) 0
A(0; 3) нү ктесі арқ ылы ө тетін 3x-2y+7=0 тү зуіне параллель болатын тү зутең деуі: C) 3x-2y=-6 D) 3(x+2)=2y E) 
A(-1; 3) жә не B(2; 3) нү ктелері арқ ылы ө тетін тү зудің тең деуі: C)y=3 D 
 E) y-3=0
E) y-3=0
A(2, 2) жә не B(5, -2) нү ктелері берілген.  кесіндісінің ортасының ординатасы: B)0D)бү тін сан
кесіндісінің ортасының ординатасы: B)0D)бү тін сан
|
|
|
A(2, 2) жә не B(5, -2) нү ктелері берілген  . кесіндісінің ортасының абциссасы: B)3, 5 C)теріс емес сан
. кесіндісінің ортасының абциссасы: B)3, 5 C)теріс емес сан
A(2, 2)жә не B(5, -2)нү ктелері берілген  векторының абциссасы: C)оң сан
векторының абциссасы: C)оң сан
A(2; -1; 4) жә не B(3; 2; -1) нү ктелері арқ ылы ө тетін сонымен бірге x+y+2z-3=0 жазық тығ ына перпендикуляр болатын жазық тық A)11x-7y-2z-21=0 D)11x-7y-2z=21 E)11(x-2)-7(y+1)-2(z-4)=0
Ax+By+Cz+5=0 жә не 2x-3y+z+5=0 жазық тық тарыA, B, C-ның сә йкес параллель мә ндері: B) 2, -3, -1 D) -6, 9, -3 E) 4, -6, 2
Айнымалылары ажыратылатын дифференциалдық тең деу: A) 
Айнымалылары ажыратылатын дифференциалдық тең деу: B)  F)
F) 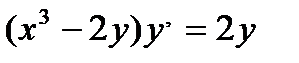 G)
G) 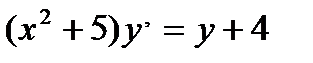
Анық талғ ан интегралдың негізгі қ асиеттері: A) 
Анық талмағ ан интегралдың негізгі қ асиеттері: A)  E )
E ) 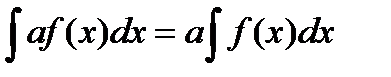 мұ ндеғ ы а тұ рақ ты F)
мұ ндеғ ы а тұ рақ ты F) 
Анық тауышты есепте 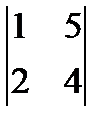 : A)-12/2
: A)-12/2
Анық тауышты есепте:  : C) 10/2 D)5 E)25/5
: C) 10/2 D)5 E)25/5
Айнымалылары ажыратылатын дифференциалдық тең деу. А)  В)
В)  C)
C) 
Ақ иқ ат емес оқ иғ аның ық тималдығ ы неге тең. A)0 B)0/3 C)0/2
Ақ иқ ат оқ иғ аның ық тималдығ ы неге тең? A)1 B)2/2 C) 
Алты ұ пайдың пайда болу ық тималдығ ы 1/6-ғ а тең болса, онда пайда болмау ытималдығ ы неге тең: A)5/6 B)  C)
C) 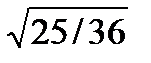
Анық тауышты есепте  А) -12 В) -48/4 С) -24/2
А) -12 В) -48/4 С) -24/2
Aнық тауышты есепте  А) 5 В) 10/2 С) 25/5
А) 5 В) 10/2 С) 25/5
Анық тауышты есепте 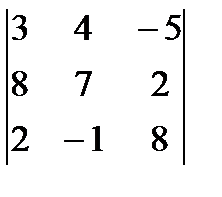 А) 88/2=В) 22*2 C) 44
А) 88/2=В) 22*2 C) 44
Анық тауышты есепте: 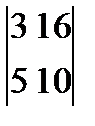 : А) -50
: А) -50
Анық тауышты есепте:  А) 20/2В)30/3 C) 10
А) 20/2В)30/3 C) 10
Анық тауышты есепте:  А) 22/2В) 33/3С) 11
А) 22/2В) 33/3С) 11
Анық тауышты есепте:  А) 24/2В) 48/4С)12
А) 24/2В) 48/4С)12
Анық тауышты есептең із.  A) 30
A) 30
Анық тауышты есептең із.  A) 5
A) 5
Анық тауышты есептең із.  А) 26
А) 26
Анық тауыштың негізгі қ асиеттері: А) егер параллель екі қ атар жолды орындарын ауыстырсақ, онда анық тауыш таң басы қ арама-қ арсығ а ауысады. В) егер анық тауыштың бас диоганалы нө лге тең болса, онда анық тауыш нө лге тең; С) Егер анық тауыштың тік жол элементтері сә йкес жатық жол элементтеріне пропорциональ болса, онда анық тауыш нө лге тең; D) Берілген анық тауышты қ андайда бір 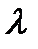 санына кө бейтсек, онда анық тауыштың барлық элементі сол санғ а кө бейтіледі.
санына кө бейтсек, онда анық тауыштың барлық элементі сол санғ а кө бейтіледі.
|
|
|
 ,
,  векторлардың скаляр кө бейтіндісін табың дар. A) -9 B)-18/2
векторлардың скаляр кө бейтіндісін табың дар. A) -9 B)-18/2
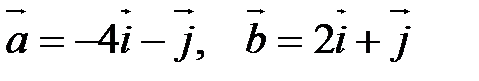 векторларынан қ ұ ралғ ан параллелограмның ауданы: A) 6/3 B)4/2 C)2
векторларынан қ ұ ралғ ан параллелограмның ауданы: A) 6/3 B)4/2 C)2
 векторының ұ зындығ ын табың дар. A)
векторының ұ зындығ ын табың дар. A) 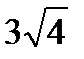 B)6
B)6
 векторының ұ зындығ ын табың дар. A) 75/3 B)50/2 C)25
векторының ұ зындығ ын табың дар. A) 75/3 B)50/2 C)25
 векторының ұ зындығ ын табың дар. A) 26/2 B)13 C)39/3
векторының ұ зындығ ын табың дар. A) 26/2 B)13 C)39/3
 векторының ұ зындығ ын табың дар.. A) 26/2 B)13 C)39/3
векторының ұ зындығ ын табың дар.. A) 26/2 B)13 C)39/3
 векторының ұ зындығ ын табың дар. A ) 7 B)14/2 C)28/4
векторының ұ зындығ ын табың дар. A ) 7 B)14/2 C)28/4
 векторының ұ зындығ ын табың дар. A) 7 B)14/2 C)28/4
векторының ұ зындығ ын табың дар. A) 7 B)14/2 C)28/4
 векторының ұ зындығ ын табың дар. A)28/2 B)42/3 C)14
векторының ұ зындығ ын табың дар. A)28/2 B)42/3 C)14
 векторының модулiн тап. A)
векторының модулiн тап. A) 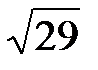
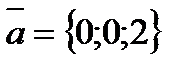 векторының модулін тап А) 2
векторының модулін тап А) 2
 векторының
векторының  ө сімен жасайтын бұ рышы
ө сімен жасайтын бұ рышы  болса, онда: А)
болса, онда: А)  В)
В) 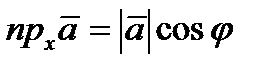 C)
C) 
 ,
,  ,
,  векторлардың аралас кө бейтіндісін табың дар. A) 7
векторлардың аралас кө бейтіндісін табың дар. A) 7
 векторларының скаляр кө бейтіндісі: В)
векторларының скаляр кө бейтіндісі: В)  E)
E) 
 векторының ұ зындығ ы тең: C)2E)
векторының ұ зындығ ы тең: C)2E) 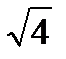 F)
F) 
 жә не
жә не 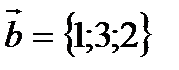 векторларының скалярлық кө бейтіндісінің мына аралық та: C)
векторларының скалярлық кө бейтіндісінің мына аралық та: C) 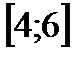
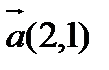 жә не
жә не  векторларының скаляр кө бейтіндісі: B)
векторларының скаляр кө бейтіндісі: B)  D
D 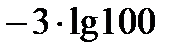 E)
E) 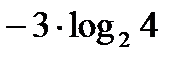
 ,
,  векторлардың скаляр кө бейтіндісін табың дар. A) 22 B)66/3
векторлардың скаляр кө бейтіндісін табың дар. A) 22 B)66/3
 ,
,  векторлардың скаляр кө бейтіндісін табың дар. A) 0 B)0/1
векторлардың скаляр кө бейтіндісін табың дар. A) 0 B)0/1
 ,
, 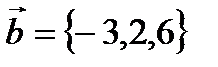 векторлардың скаляр кө бейтіндісін табың дар. A) 10 B)30/3
векторлардың скаляр кө бейтіндісін табың дар. A) 10 B)30/3
 ,
, 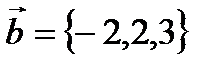 векторлардың скаляр кө бейтіндісін табың дар. A) 13 B)39/3
векторлардың скаляр кө бейтіндісін табың дар. A) 13 B)39/3
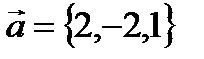 ,
, 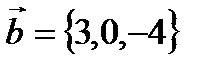 векторлардың скаляр кө бейтіндісін табың дар. A) 2 B)6/3
векторлардың скаляр кө бейтіндісін табың дар. A) 2 B)6/3
 ,
,  векторлардың скаляр кө бейтіндісін табың дар. A) -4 B)-8/2
векторлардың скаляр кө бейтіндісін табың дар. A) -4 B)-8/2
 ,
,  векторларының скаляр кө бейтіндісін табың дар. A) 17 B)51/3 C)34/2
векторларының скаляр кө бейтіндісін табың дар. A) 17 B)51/3 C)34/2
 ,
, 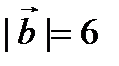 ,
,  векторлардың скаляр кө бейтіндісін табың дар. A) 9 B)18/2
векторлардың скаляр кө бейтіндісін табың дар. A) 9 B)18/2
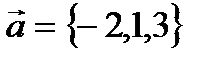 ,
,  ,
,  векторлардың аралас кө бейтіндісін табың дар. A) 44 B) 88/2 C) 132/3
векторлардың аралас кө бейтіндісін табың дар. A) 44 B) 88/2 C) 132/3
 ,
,  ,
,  векторлардың аралас кө бейтіндісін табың дар. A) -58/2 B)-87/3 C)-29
векторлардың аралас кө бейтіндісін табың дар. A) -58/2 B)-87/3 C)-29
 ,
,  ,
,  векторлардың аралас кө бейтіндісін табың дар. A) 38/2 B) 19 C) 57/3
векторлардың аралас кө бейтіндісін табың дар. A) 38/2 B) 19 C) 57/3
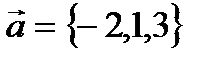 ,
,  ,
,  векторлардың аралас кө бейтіндісін табың дар. A) 44
векторлардың аралас кө бейтіндісін табың дар. A) 44
 ,
, 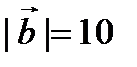 ,
,  векторлардың скаляр кө бейтіндісін табың дар. A) 15 B)30/2
векторлардың скаляр кө бейтіндісін табың дар. A) 15 B)30/2
 ,
, 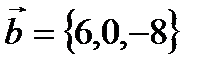 векторлардың скаляр кө бейтіндісін табың дар. A) 4 B)8/2
векторлардың скаляр кө бейтіндісін табың дар. A) 4 B)8/2
 векторының ұ зындығ ын табың дар. A) 11 B)22/2
векторының ұ зындығ ын табың дар. A) 11 B)22/2
|
|
|
 векторының ұ зындығ ын табың дар. A) 5 B)20/4 C)10/2
векторының ұ зындығ ын табың дар. A) 5 B)20/4 C)10/2
 дә режелік қ атарының жинақ тылық радиусын тең: A)
дә режелік қ атарының жинақ тылық радиусын тең: A)  B)
B)  C)
C) 
 векторының модулiн тап. A)
векторының модулiн тап. A) 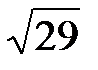
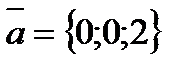 векторының модулін тап А) 2
векторының модулін тап А) 2
 векторының
векторының  ө сімен жасайтын бұ рышы
ө сімен жасайтын бұ рышы  болса, онда: А)
болса, онда: А)  В)
В) 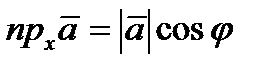 C)
C) 
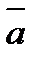 жә не
жә не  векторларының векторлық кө бейтіндісі деп тө мендегі шарттарды қ анағ аттандыратын
векторларының векторлық кө бейтіндісі деп тө мендегі шарттарды қ анағ аттандыратын 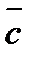 векторын айтады А) осы векторлармен реттелген сол ү штік қ ұ райды В)
векторын айтады А) осы векторлармен реттелген сол ү штік қ ұ райды В) 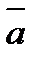 векторына да
векторына да  векторына да перпендикуляр С) ұ зындығ ы
векторына да перпендикуляр С) ұ зындығ ы 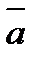 жә не
жә не  векторларынан қ ұ рылғ ан параллелограммның ауданына тең
векторларынан қ ұ рылғ ан параллелограммның ауданына тең
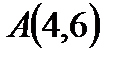 жә не
жә не  нү ктелері арқ ылы ө тетін тү зудің бұ рыштық коэффициентін табу керек: А)
нү ктелері арқ ылы ө тетін тү зудің бұ рыштық коэффициентін табу керек: А)  В)2 С)
В)2 С) 
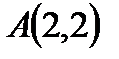 жә не
жә не  нү ктелері берілген.
нү ктелері берілген. 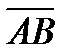 векторының ординатасы: А)-4
векторының ординатасы: А)-4
 жә не
жә не 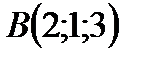 нү ктелерінің арақ ашық тығ ын табу керек: А) 9/3В) 3
нү ктелерінің арақ ашық тығ ын табу керек: А) 9/3В) 3
А(-1; 3) жә не В(2; 3)нү ктелері арқ ылы ө тетін тү зудің тең деуі: А)  В)
В) 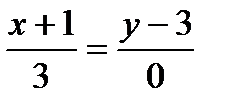 С)
С) 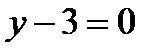
А(-3, 1), В(0, 5) нү ктелері берілген.  векторының координаталары тең: А) (-3; -4) B) (-9/3; -16/4)
векторының координаталары тең: А) (-3; -4) B) (-9/3; -16/4)
А(-3, 1), В (0, 5) нү ктелері берілген.  векторының координаталары тең: А) (3; 4)
векторының координаталары тең: А) (3; 4)
А(3, 3, 5) жә не В(2, 1, 3) нү ктелерінің арақ ашық тығ ын табың дар. A) 3 B) 
А(4, 6) жә не В(–1, -4) нү ктелері арқ ылы ө тетін тү зудің бұ рыштық коэффициентін табың дар. A) 2 B)  C)
C) 
 векторының ұ зындығ ы: A)
векторының ұ зындығ ы: A) 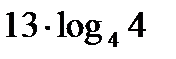 B)
B) 
ББББББББББ
Берілген сызық ты тең деулер жү йесін шешу арқ ылы y айнымалысының мә нін табың ыз: 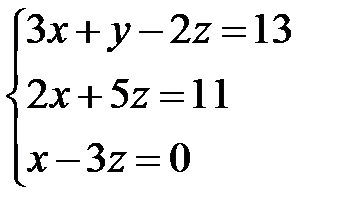 A) 6
A) 6
Берілгені. D(Х)=4. Табың ыз:  . A)
. A)  B)4/2 C)2
B)4/2 C)2
Берілгені:  . Табың ыз:
. Табың ыз:  . А) -20 B)-60/3 C)-40/2
. А) -20 B)-60/3 C)-40/2
Берілгені:  . Табың ыз:
. Табың ыз:  . А) -40 B)-80/2 C)-120/3
. А) -40 B)-80/2 C)-120/3
Берілгені: 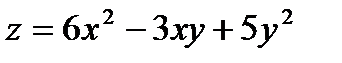 . Табың ыз:
. Табың ыз:  A) 12 B)36/3
A) 12 B)36/3
Берілгені:  табу керек:
табу керек:  А)2 В)4/2 С) 6/3
А)2 В)4/2 С) 6/3
Берілгені:  . Табу керек:
. Табу керек:  А)
А)  В -3
В -3
Берілгені: 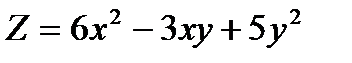 . Табу керек:
. Табу керек:  А) 24/2В) 12 C) 36/3
А) 24/2В) 12 C) 36/3
Берілгені:  . Нү ктесіндегі
. Нү ктесіндегі  мә нін табың ыз: A) 4B)
мә нін табың ыз: A) 4B) 
Берілгені:  . Табың ыз:
. Табың ыз: 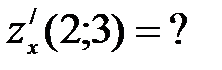 A)4 B)
A)4 B)  C)
C) 
Берілгені: Дано. 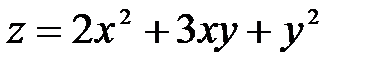 . Нү ктесіндегі
. Нү ктесіндегі 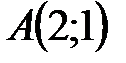
 -ті табың ыз: A)
-ті табың ыз: A)  B)
B) 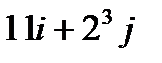 C)
C) 
Берілгені: А= 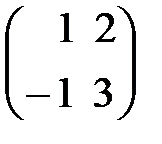 . Берiлген матрицаның А2 тап. . A)
. Берiлген матрицаның А2 тап. . A)  B)
B)  C)
C) 
Берілгені: А= 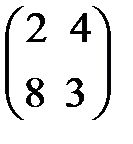 , В=
, В=  . Берiлген матрицалардың кө бейтіндісін тап. A)
. Берiлген матрицалардың кө бейтіндісін тап. A) 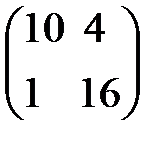 B)
B)  C)
C) 
Бірінші ретті сызық тық дифференциалдық тең деу: А) 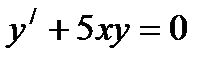 В)
В) 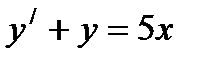
Бірінші ретті сызық тық дифферециалдық тең деу: А)  В)
В)  С)
С) 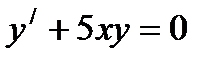
Болатын гиперболаның тең деуі А)  В)
В) 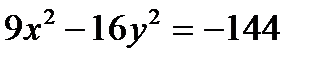
Берілген  ;
;  ;
;  ;
; 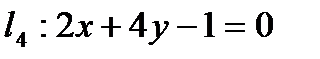 ;
;  жә не
жә не 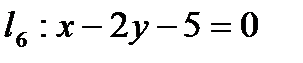 тү зулерінің арасында ө зара параллель болатын тү зулер: B)
тү зулерінің арасында ө зара параллель болатын тү зулер: B) 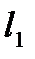 жә не
жә не 
Берілгені 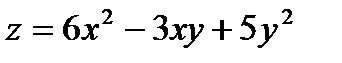 табу керек
табу керек  : A)12 G)36/3
: A)12 G)36/3
Берілгені: 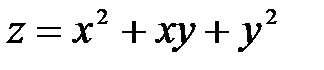 табу керек:
табу керек: 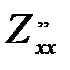 B)6/3 D)2 G)4/2
B)6/3 D)2 G)4/2
Бірінші ретті сызық тық дифференциялдық тендеу: E)  F)y+y=5x
F)y+y=5x
|
|
|


