 |
Ммммммннннн. Оооооооорррррр. Сссссссттттттт
|
|
|
|
ММММММННННН
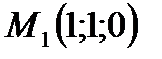 ,
,  екі нү ктеніің арақ ашық тығ ын тап: А)
екі нү ктеніің арақ ашық тығ ын тап: А) 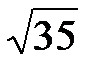 В)
В) 
 нү ктесінде
нү ктесінде  -нің мә ні, егер
-нің мә ні, егер  : А) -1
: А) -1
 нү ктесінен
нү ктесінен  осіне тү сірілген перпендикуляр тең деуі: А)
осіне тү сірілген перпендикуляр тең деуі: А) 
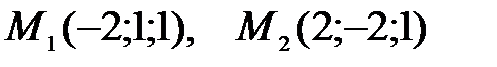 екi нү ктенiң арақ ашық тығ ын тап. A) 5
екi нү ктенiң арақ ашық тығ ын тап. A) 5
M0(-2; 1; -1)Нү ктесі арқ ылы ө тетін S={1; -2; 3}векторына параллель болатын тү зудің параметрлік тең деуі: D)x=-2+t, y=1-2t, z=-1+3tE)x+2=t, y-1=-2t, z+1=3tF) 
М  (1, -2, 3) нү ктесі арқ ылы ө тетін жә не
(1, -2, 3) нү ктесі арқ ылы ө тетін жә не  векторына перпендикуляр тү зудің тең деуі. A)
векторына перпендикуляр тү зудің тең деуі. A) 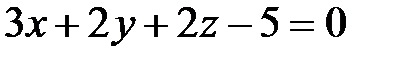
М(1; -2) нү ктесінде  - ті табың ыз, егер
- ті табың ыз, егер  . A)-1 B) -
. A)-1 B) - 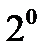
М1(1; 1; 0), М2(-4; 0; 3) екi нү ктенiң арақ ашық тығ ын тап. А)  B)
B) 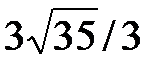 C)
C) 
М1(-1; 2; 3), М2(3; -4; 2) екi нү ктенiң арақ ашық тығ ын тап. . А)  B)
B)  C)
C) 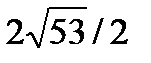
М1(3; 2; 1), М2(4; -3; 2) екi нү ктенiң арақ ашық тығ ын тап. А)  B)
B)  C)
C) 
Матрицаның А13 алгебралық толық тауышын есепте  А)
А) 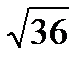 B)6
B)6
Матрицаның А21 алгебралық толық тауышын есепте.  А)–2 B)-4/2
А)–2 B)-4/2
Матрицаның А22 алгебралық толық тауышын есепте.  А)8 B)16/2
А)8 B)16/2
Матрицаның М11 минорын тап.  А)30 B)
А)30 B) 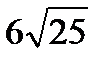
Матрицаның М12 минорын тап.  A) 12 B)48/4
A) 12 B)48/4
Матрицаның М13 минорын тап.  A) 6 B)12/2
A) 6 B)12/2
Матрицаның М21 минорын тап.  A)2 B)4/2
A)2 B)4/2
Матрицаның рангісін анық таң ыз. 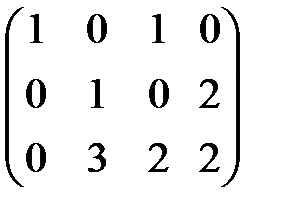 : A)
: A) 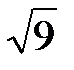 B)3
B)3
Матрицаның рангы мына жағ дайларда ө згермейді: А) Кез-келген екі жолын (бағ анын)) ауыстырғ анын. В) Кез-келген жолының (бағ анының ) элементтерін 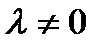 санына кө бейткеннен. С) Кез-келген қ атардың элементтерін
санына кө бейткеннен. С) Кез-келген қ атардың элементтерін 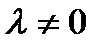 санына кө бейтілген басқ а қ атардың элементтерін қ осқ аннан.
санына кө бейтілген басқ а қ атардың элементтерін қ осқ аннан.
Матрицаның рангы мына жағ дайларда ө згермейді: А) Кез-келген жолының (бағ анның ) элементтерін  санына кө бейткеннен. В) Кез-келген элементтерін басқ а сандармен ауыстырғ аннан. С) Кез-келген элементтеріне
санына кө бейткеннен. В) Кез-келген элементтерін басқ а сандармен ауыстырғ аннан. С) Кез-келген элементтеріне  санына кө бейтілген басқ а қ атардың элементтерін қ осқ аннан.
санына кө бейтілген басқ а қ атардың элементтерін қ осқ аннан.
|
|
|
Матрицанынң рангы мына жағ дайларда ө згермейді: C)кез келген жолының бағ анының элементтерін 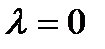 санына кө бейткеннен E)кез-келген екі жолын бағ анын ауыстырғ аннан
санына кө бейткеннен E)кез-келген екі жолын бағ анын ауыстырғ аннан
Мына матрицаү шін кері матрицаны табуғ а болады: B)  E
E 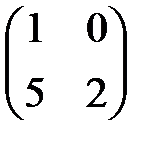
Мына матрица ү шін кері матрицаны табуғ а болады: А)  В)
В) 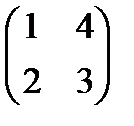 С)
С) 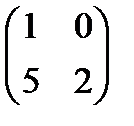
Мына ө лшемді матрицалардың кө бейтіндісін табуғ а болады: B) 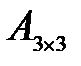 жә не
жә не 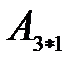
Нақ ты осі  , ал эксцентриситеті
, ал эксцентриситеті  болатын гипербола тең деуі А)
болатын гипербола тең деуі А) 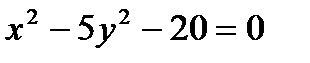 В)
В) 
Нақ ты осі 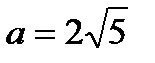 , ал эксцентриситеті
, ал эксцентриситеті  болатын гипербола тең деуі: A)
болатын гипербола тең деуі: A) 
Негізгі интегралдар кестесінің формуласы: E) 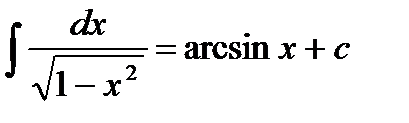 G)
G) 
ООООООООРРРРРР
Ойын сү йегі лақ тырылды. Жұ п ұ пайлар тү су ық тималдығ ын табың ыз: A)0, 5 B)1/2
Ойын сү йегі лақ тырылды. Тақ ұ пайлар тү су ық тималдығ ын табың ыз: A)0, 5 B)1/2
Орташа квадраттық ауытқ у  тең болса, онда дисперсияны табың ыз. A)
тең болса, онда дисперсияны табың ыз. A)  B)
B) 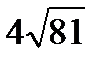 C)36
C)36
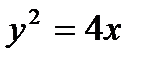 параболасы ү шін: А) тө бесі
параболасы ү шін: А) тө бесі 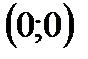
Радиусы  , центрі
, центрі 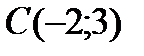 нү ктесінде жатқ ан шең бердің тең деуі: А)
нү ктесінде жатқ ан шең бердің тең деуі: А) 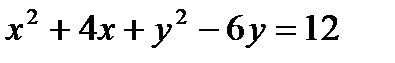 В)
В) 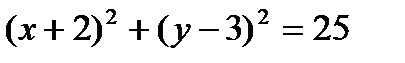 С)
С) 
СССССССТТТТТТТ
Скаляр кө бейтіндінің қ асиеттері А)  В)
В) 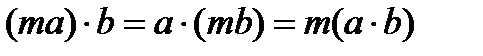
Скалярлық кө бейтіндісінің қ асиеттері: A) 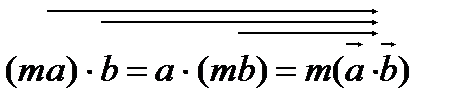 B)
B) 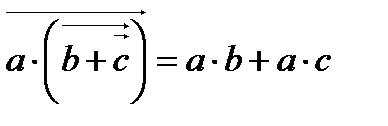 D)
D) 
Сызық тармен шектелген фигураның ауданын табу керек 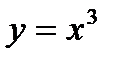 ,
, 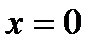 ,
, 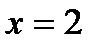 ,
,  А)8/2 В)4 С) 12/3
А)8/2 В)4 С) 12/3
Сызық тармен шектелген фигураның ауданын табу керек 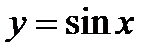 ,
, 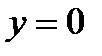 ,
, 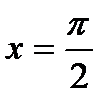 ,
,  А) 1В) 8/8
А) 1В) 8/8
Сызық тармен шектелген фигураның ауданын табу керек  А) 128/2 В) 192/3 С) 64
А) 128/2 В) 192/3 С) 64
Сызық тармен шектелген фигураның ауданын табу керек  А) 30/5В) 6
А) 30/5В) 6
Сызық тармен шектелген фигураның ауданын табың ыз:  A) 1 B)2/2
A) 1 B)2/2
Сызық тармен шектелген фигураның ауданын табың ыз: 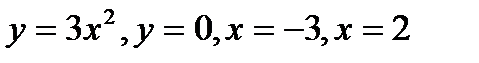 A) 35 B)70/2
A) 35 B)70/2
Сызық тармен шектелген фигураның ауданын табың ыз:  A) 48
A) 48
Сызық тармен шектелген фигураның ауданын табың ыз:  A) 6 B)18/3
A) 6 B)18/3
|
|
|
Сызық тармен шектелген фигураның ауданын табың ыз:  A) 9
A) 9
Сызық тармен шектелген фигураның ауданын табың ыз: y=5x, x=2, y=0 A) 10
Сызық тармен шектелген фигураның ауданын табың ыз:  A) 2
A) 2
Сызық тармен шектелген фигураның ауданын табың ыз:  A) 8
A) 8
Сызық тармен шектелген фигураның ауданын табың ыз:  A) 9
A) 9
Сызық тармен шектелген фигураның ауданын табың ыз: A) 8
Тақ функция А) 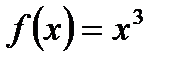 В)
В) 
Таң балары айнымалы қ атар: А) 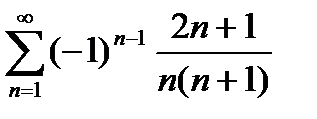 В)
В)  С)
С) 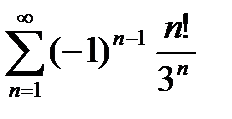
Таң балары айнымалы қ атар: С) 
Тең деуді шешің із:  . A)
. A) 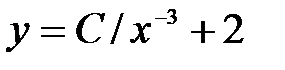 B)
B)  C)
C) 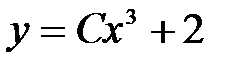
Тө белері  ,
,  жә не
жә не  нү ктелері болатын ү шбұ рыштың ауданы тең: D)
нү ктелері болатын ү шбұ рыштың ауданы тең: D) 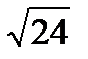 Е)
Е)  F)
F) 
Тікелей интегралдау арқ ылы табылатын интеграл: A )  B)
B) 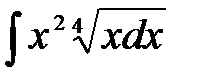 E)
E) 
Тө белері A(3; -3; 1), B(5; -2; 3) жә не C(3; -1; 3) болатын ү шбұ рыштың ауданы жататын аралық: D) 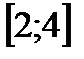 E)
E) 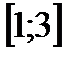
Ү Ү Ү Ү Ү Ұ Ұ Ұ Ұ ШШШШШ
Ұ яшық та 12 шар бар, оның 3 - уі ақ, 4 - уі қ аражә не 5 –у і қ ызыл. Кездейсоқ алынғ ан шардың қ ара болу ық тималдығ ын табың ыз. A)1/3 B)  C)
C) 
Ұ яшық та 15 шар бар. Оның 5 ақ, 10 қ ара шар. Екі шар алынды. Алынғ ан шардың кө к тү сті болу ық тималдығ ын табың дар. A)0
Ұ яшық та 3 қ ызыл шар бар. Кездейсоқ алынғ ан шардың ақ болу ық тималдығ ын табың ыз. A)0 B)0/4 C)0/3
Ұ яшық та 6 шар бар, оның 3 - уі қ ызыл, 2 - уі кө к жә не 1 - уі ақ. Кездейсоқ алынғ ан шардың қ ызыл болу ық тималдығ ын табың ыз. A)0, 5 B)1/2
Ү лкен жарты осі 5-ке жә не кіші жарты осі 3-ке тең болатын эллипстің тең деуі: С)9х2+25у2-225=0; D)
Ү шінші ретті дефферециалды тең деу: A)  D)
D) 
|
|
|


