 |
Порядок выполнения работы и методические указания
|
|
|
|
Порядок выполнения работы и методические указания
1. Расчет областей значений основной погрешности вольтметров
1. 1. Построить области допускаемых основных абсолютных погрешностей аналогового и цифрового вольтметров (табл. 1. 1) в диапазоне от 0 до 2, 5 В. Пример построения показан на рис. 1. 1. Предел измерения исследуемого вольтметра выбрать равным 2, 5 В. Тогда пределы измерения эталонного вольтметра следует выбрать равными 1 или 10 В.
Указание. Для простых электроизмерительных приборов основную погрешность обычно нормируют в форме предельно допустимойприведенной погрешности – числом g, выраженным в %. Число g, записанное без указания %, определяет класс точности такого вольтметра. Область значений допускаемой основной абсолютной погрешности такого прибора можно определить с помощью простой одночленной формулы:
 , (1. 1)
, (1. 1)
здесь Uк– значение установленного предела измерения.
Видно, что эта погрешность не зависит от значения измеряемого напряжения – носит чисто аддитивный характер.
Основную погрешность более сложных и точных цифровых вольтметров обычно нормируют в форме предельно допустимой относительной погрешности, %, по двучленной формуле вида:
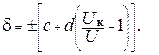 (1. 2)
(1. 2)
Значения коэффициентов c (%)и d (%), записанные через косую черту(c/d), определяюткласс точности цифрового вольтметра.
Область допускаемой основной абсолютной погрешности такоговольтметра можно вычислить по формуле:
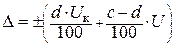 , U=[0, Uк]. (1. 3)
, U=[0, Uк]. (1. 3)
Эта погрешность растет с увеличением измеряемого напряжения, т. е. имеет, кроме аддитивной, еще и мультипликативную составляющую.
|
|
|
Специфической особенностью используемого в данной работе цифрового вольтметра В7-27 является возможность измерения напряжения до 1, 999 В при установке предела Uк = 1 В и напряжение до 19, 9 В при установке предела Uк =10 В. Изготовитель гарантирует, что при измерении напряжений U > Uк относительная погрешность будет находиться в соответствии с (1. 2) в пределах ±с (%).
Поскольку абсолютная погрешность эталонного прибора должна быть, по крайней мере, в 3 раза меньше погрешности исследуемого прибора, не следует без необходимости использовать в цифровом вольтметре В7-27 предел 10 В.
 |
Рис. 1. 1. Области значений абсолютной погрешности:
а - нормируемая для аналогового прибора,
б - нормируемая для цифрового прибора,
в - полученная экспериментально для аналогового прибора по п. 3
DUm, m = 1, 2, 3 (1. 9)
Примечание. Фирмы-изготовители вольтметров могут использовать и другие формулы для нормирования предельных погрешностей выпускаемых приборов.
1. 2. Сравнить значения абсолютных погрешностей аналогового и цифрового вольтметров в диапазоне от 0 до 2, 5 В, сделать вывод о возможности использования цифрового вольтметра в качестве эталонного на пределах 1 и 10 В.
2. Оценка систематической и случайной составляющих
основной погрешности исследуемого вольтметра
Исследование провести для трех точек установленного на исследуемом вольтметре диапазона измерения 2, 5В - для трех значений напряжения: U1=(0, 3-0, 7)В - в начале шкалы, U2 = (0, 8-1, 5)В - в середине и U3=(1, 5-1, 9)В - в конце.
2. 1. Ознакомиться с кратким описанием и органами управления вольтметров и источника постоянного напряжения. Включить питание источника постоянного напряжения и цифрового вольтметра. Проверить установку нуля аналогового и цифрового вольтметров.
2. 2. Собрать схему измерения согласно рис. 1. 2.
2. 3. Установить требуемые пределы измерения Uк на обоих вольтметрах.
|
|
|
 |
Рис. 1. 2. Схема для исследования погрешностей вольтметра
2. 4. Выбрать отметку на шкале исследуемого вольтметра, соответствующую выбранному значению напряжения U1 . Регулируя напряжение источника, установить показание равное U1, измерить действительное значение напряжения источника по показаниям эталонного вольтметра U1i и записать в табл. 1. 2 (столбец 2). Всего выполнить n измерений действительных значений напряжения U1i, i=1,..., n (8 ³ n ³ 16), каждый раз заново устанавливая показания исследуемого вольтметра на выбранную отметку шкалы.
2. 5. Повторить измерения п. 2. 4 для выбранных значений U2 и U3 . Измеренные действительные значения U2i и U3i, i =1,..., n записать в 6 и 10-й столбцы табл. 1. 2 соответственно.
2. 6. Вычислить для каждого значения напряжения U1, U2, U3 следующие величины:
2. 6. 1. Абсолютную погрешность каждого однократного измерения
 (1. 4)
(1. 4)
и записать их значения в 3, 7 и 11-й столбцы, внизу каждого столбца поместить алгебраическую сумму 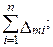
2. 6. 2. Оценку систематической составляющей погрешности 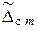 , вычислив ее значение как среднее значение погрешности
, вычислив ее значение как среднее значение погрешности 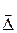 m:
m:
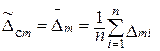 (1. 5)
(1. 5)
2. 6. 3. Случайные составляющие погрешности каждого измерения:
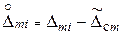 (1. 6)
(1. 6)
и записать их значения в 4, 8 и 12-й столбцы.
2. 6. 4. Оценки среднего квадратического отклонения случайной составляющей погрешности (среднюю квадратическую погрешность) однократного измерения для трех выбранных точек шкалы исследуемого вольтметра:

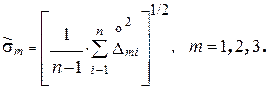 (1. 7)
(1. 7)
Для этого найти квадраты случайных составляющих 
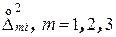 , i=1,..., n и полученные числа занести в 5, 9 и 13-й столбцы, а внизу каждого из них поместить суммы этих квадратов
, i=1,..., n и полученные числа занести в 5, 9 и 13-й столбцы, а внизу каждого из них поместить суммы этих квадратов 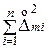 , m=1, 2, 3. Найденные значения оценок
, m=1, 2, 3. Найденные значения оценок 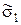 ,
, 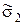 и
и 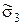 также поместить в табл. 1. 2.
также поместить в табл. 1. 2.
Таблица 1. 2
Результаты измерений и расчета составляющих основной погрешности
исследуемого вольтметра
| i | U1 = 0, 5 B | U2 = 1, 0 B | U3 = 1, 5 B | ||||||||||||
| Ui | 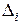
| 
| 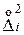
| Ui | 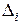
| 
|
| Ui | 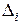
| 
| 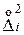
| ||||
|
| |||||||||||||||
|
| |||||||||||||||
| × |
| ||||||||||||||
| × |
| ||||||||||||||
| × |
| ||||||||||||||
| i |
| ||||||||||||||
|
| |||||||||||||||
| × |
| ||||||||||||||
| × |
| ||||||||||||||
| n |
| ||||||||||||||
|
| S= | S = | S = | S = | S = | S = | |||||||||
|
|
|
| |||||||||||||
| | | | |||||||||||||
| Рдов= , n = , t = | |||||||||||||||
| Dдов1= ± В | Dдов2= ± В | Dдов3= ± В | |||||||||||||
2. 6. 5. Доверительные интервалы случайной погрешности однократного измерения в предположении, что закон распределения этой случайной погрешности - нормальный:
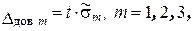 (1. 8)
(1. 8)
где t - коэффициент Стьюдента, значение которого зависит от заданного значения доверительной вероятности Рдов и числа проведенных измерений n. Значения t взять из таблицы распределения Стьюдента (прил. 1). При обработке результатов простых технических измерений доверительную вероятность обычно выбирают в пределах от 0, 8 до 0, 9.
Указание . Английский исследователь Госсет (опубликовавший свою знаменитую работу под псевдонимом Стьюдент) в 1908 г. показал, что если оценка среднеквадратического отклонения получена по небольшому числу измерений (n £ 17), то доверительный интервал для случайной величины с нормальным законом распределения следует рассчитывать с использованием распределения, которое впоследствии получило его имя - распределение Стьюдента. При увеличении числа измерений, распределение Стьюдента сходится к нормальному распределению. Поэтому, если число измерений велико, при оценке доверительного интервала можно использовать таблицы интеграла вероятности.
|
|
|
|
|
|






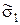 = В
= В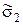 = В
= В