5. Измерение параметров двухполюсников

5. Измерение параметров двухполюсников

с помощью измерителя добротности

3. 1. Включить питание прибора Е4-11. Ознакомиться с его органами управления, схемой и расположением клемм для подключения измеряемых элементов. В соответствии с требованиями технического описания прибора установить переключатель ПРЕДЕЛЫ Q в положение НУЛЬ Q и его регулировкой установить нуль на шкале Q. Установить частоту 30 МГц (первый поддиапазон 30-50 МГц), установить переключатель ПРЕДЕЛЫ Q в положение КАЛИБР. Q и его регулировкой ручкой установить стрелку шкалы Q на знак.

Указание. Измеритель добротности (куметр) реализует резонансный метод измерения параметров двухполюсников (рис. 2. 3).

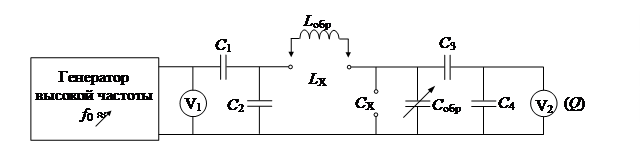В измерительный контур, образованный L_обр и C_обрчерез емкостный делитель С₁, С₂ вводится напряжение U₀, контролируемое вольтметромV₁. ВольтметрV₂служит индикатором резонанса.

 

 

Рис. 2. 3. Упрощенная структурная схема измерителя добротности

 

Поскольку при резонансе если Q > 10, имеет место равенство

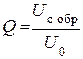,                                            (2. 4)

а величина U₀поддерживается постоянной, то можно проградуировать шкалу вольтметраV₂ в единицах Q. В результате получим прямые измерения добротности.

При резонансе справедливо соотношение

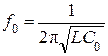,                                       (2. 5)

поэтому, зная частоту генератора f₀и емкость колебательного контура С₀, можно оценить неизвестное значение индуктивности L. Такие измерения называют косвенными.

С помощью куметра можно реализовать на заданной и достаточно высокой частоте также косвенные измерения емкости С_x, сопротивления потерь конденсаторов R_C, tgd, R_x и т. п. Такие измерения, как правило, проводятся в два этапа. Сначала колебательный контур прибора настраивают в резонанс и оценивают его характеристики в исходном состоянии. Затем в контур подключают исследуемый двухполюсник и по изменению характеристик контура оценивают параметры подключенного двухполюсника, используя формулы (2. 6) - (2. 16).

3. 2. Измерить действующие значения индуктивности L_д и добротности Q_д катушки индуктивности.

Подключить измеряемую катушку к зажимам L_x, расположенным на верхней панели измерителя добротности. Установить частоту генератора измерителя добротности, значение которой f₁ указано на корпусе измеряемой катушки индуктивности. Настроить измерительный контур в резонанс на частоте f₁ регулировкой емкости образцового конденсатора по максимуму показания вольтметра, градуированного в значениях Q.

Записать значения установленной частоты f₁, емкости образцового конденсатора С_об1 и добротности Q_д1 на частоте f₁ в табл. 2. 3. (С_об1= С_об (f₁), Q_д1=Q_д(f₁)). Значение С_об1 следует записать с учетом разрешающей способности шкалы образцового конденсатора 0, 01 пФ.

Таблица 2. 3

Результаты оценки параметров катушки индуктивности

Частота, MГц	Qд	Cоб, пФ	Lд, мкГн	Rд, Ом	CL, пФ	Lx, мкГн	Qx	RL, Ом	fL, МГц
f1
f2

 

Вычислить и записать в табл. 2. 3 действующее значение индуктивности

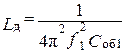                                   (2. 6)

и действующее сопротивление потерь в измеряемой катушке

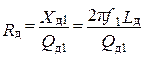.                              (2. 7)

3. 3. Оценить паразитную емкость, которую катушка индуктивности вносит в колебательный контур.

Установить частоту генератора f₂ = 2f₁. Настроить измерительный контур в резонанс и записать в табл. 2. 3 полученные значения f₂, С_об2 и Q_д2.

Вычислить собственную емкость катушки С_L из (2. 9) или (2. 10), результат внести в табл. 2. 3. Оценить истинное значение индуктивности по формуле (2. 11) и ее собственную резонансную частоту по формуле (2. 12).

Указание . Истинное значение индуктивности отличается от действующего вследствие того, что катушка вносит в контур паразитную емкость C_L, которую можно оценить по результатам настройки измерительного контура в резонанс на двух частотах путем решения системы двух уравнений с двумя неизвестными

                                 

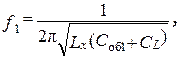
(2. 8)

                                              

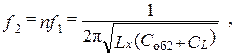
гдеС_об1, С_об2 - показания шкалы образцового конденсатора при резонансе на частотах f₁и f₂, соответственно. Решая систему уравнений относительно С_L, получаем:

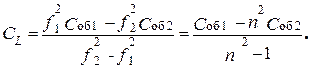                       (2. 9)

Удобно выбрать n = 2, тогда (2. 9) упрощается:

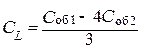.                                                     (2. 10)

Теперь можно оценить истинное значение индуктивности

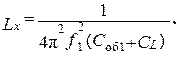                                  (2. 11)

Для проверки корректности этого результата следует повторить расчет L_x, подставив в (2. 11) значения f₂и C_об2. Два полученных значения L_x должны совпадать в пределах погрешностей косвенных измерений индуктивности (п. 3. 4. ).

Полученное значение C_L позволяет оценить собственную резонансную частоту исследуемой катушки индуктивности

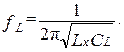                                    (2. 12)

3. 4. Измерить емкость конденсатора С_х и тангенс угла потерь.

Подключить к зажимам L_x штатную катушку индуктивности, входящую в комплект прибора Е4-11. Установить частоту генератора измерителя добротности, значение которой f₁ указано на корпусе измеряемой катушки индуктивности. Настроить измерительный контур в резонанс на частоте f₁ регулировкой емкости образцового конденсатора по максимуму показания вольтметра, градуированного в значениях Q. Записать значения установленной емкости С_об1, резонансной частоты f, и добротности Q₁ в табл. 2. 4.

Таблица 2. 4

Результаты измерений параметров конденсатора и резистора

Объект измерения	f, МГц	Соб1, пФ	Q1	Cоб2, пф	Q2	Cx, пф	tgd	Rx, Ом	СR, пф
Конденсатор								-	-
Резистор						-	-

 

Подключить к зажимам С_х измеряемый конденсатор (параллельно образцовому конденсатору) и изменением емкости образцового конденсатора восстановить резонанс на частоте f. Записать новые значения С_об2 и Q₂ в табл. 2. 4. Вычислить и поместить в табл. 2. 4 результаты косвенных измерений емкости конденсатора

С_х = С_об1 – С_об2                                              (2. 13)

и тангенса угла потерь                                                      (2. 14)

Указание . Чем больше установленное значение начальной емкости C_об1, тем шире диапазон измерения неизвестной емкости C_x. Поскольку нормируемая погрешность образцового конденсатора имеет существенную мультипликативную составляющую, при измерении емкости C_x целесообразно устанавливать минимально возможное значение начальной емкости С_об1.

3. 5. Измерить сопротивление резистора и его паразитную емкость.

Указание. Эквивалентные схемы конденсатора и резистора на высоких частотах одинаковы, поэтому процедура измерения параметров резистора не отличается от процедуры измерения параметров конденсатора.

После выполнения двух настроек в резонанс (без измеряемого резистора и при его подключении) записать полученные значения f, С_об1, Q₁, C_об2 и Q₂ в табл. 2. 4 и вычислить сопротивление резистора

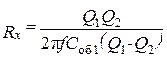                           (2. 15)

и его паразитную емкость         С_R = C_об1 – С_об2.                                (2. 16)

3. 6. Вывести формулы для оценки абсолютных Δ L_x, Δ C_x, Δ R_x или относительных d_L, d_с, d_R погрешностей косвенных измерений индуктивности катушки, емкости конденсатора и сопротивления резистора с помощью измерителя добротности на основе функциональных зависимостей (2. 6), (2. 13), (2. 15), определяющих измеряемые параметры (результаты расчета поместить в табл. 2. 5).

Таблица 2. 5

Оценка основной абсолютной погрешности

измерения параметров двухполюсников с помощью измерителя добротности

Измеряемая величина	Полученное значение	Относительная погрешность, %	Абсолютная погрешность	Результат измерения
Lx, нГн
Q
Сх, пФ
RС, кОм
Rx, кОм
СR , пФ

Указание. Главными источниками погрешностей косвенных измерений параметров двухполюсников с помощью куметра являются погрешности входящих в соответствующие формулы аргументов, которые оценивают с помощью прямых измерений - по шкалам Q, f и C₀этого прибора:

· погрешность измерения добротности D_Q,

· погрешность установки частоты генератора D_f ,

· погрешность градуировки образцового конденсатора D_C  .

Эти погрешности указаны в метрологических характеристиках прибора.

Если Y - искомая величина, связанная функциональной зависимостью

Y=F(x₁ , …, x_i, …, x_n)

с величинами x_i (i=1,..., n), которые измеряют непосредственно, то соотношение

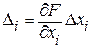                                     (2. 17)

позволяет оценить частную абсолютную погрешность косвенного измерения величины Y, обусловленную погрешностьюDx_i аргумента x_i.

Выражение для абсолютной погрешности косвенного измерения, полученное путем дифференцирования, в некоторых случаях может получиться достаточно громоздким. Тогда целесообразно использовать выражение для частной относительной погрешности косвенного измерения

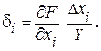                                                      (2. 18)

При этом формулы значительно упрощаются (сокращаются постоянные коэффициенты).

Способ оценки результирующей (суммарной) погрешности косвенного измерения при наличии нескольких аргументов зависит от свойств исходных погрешностейDx_i.

Если это систематические погрешности, то частные погрешности косвенных измерений складывают алгебраически с учетом знака. При этом отдельные систематические погрешности косвенных измерений могут друг друга частично компенсировать.

Если погрешности исходных величин носят случайный характер, взаимонезависимы и известны их средние квадратические отклонения, то абсолютная средняя квадратическая погрешность косвенного измерения определяется соотношением

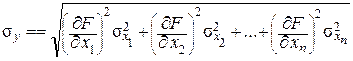.               (2. 19)

Погрешности прямых измерений с помощью куметра(D_Q, D_f, D_C)обычно задают симметричными интервалами как пределы неисключенных систематических погрешностей. В этом случае предельную погрешность косвенного измерения при количестве составляющих не более 3 принято определять путем суммирования модулей соответствующих частных абсолютных или относительных погрешностей

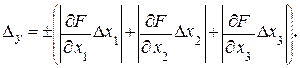                        (2. 20)

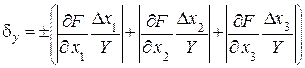.                               (2. 21)

Например, если частная относительная составляют, соответственно, δ ₁=±1%, δ ₂=±2%, δ ₃=±3% то результирующая предельная погрешность косвенного измерения будет находиться в пределах ±6%.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: