Главная | Обратная связь | Поможем написать вашу работу!

Методы, виды и способы отбора выборочных совокупностей

В теории выборочного наблюдения разработаны различные методы, способы и виды отбора единиц из генеральной совокупности. По методам отбор делится на повторный и бесповторный.

При повторном отборе каждая единица, отобранная в случайном порядке, после ее обследования возвращается в генеральную совокупность и в последующем отборе может снова попасть в выборку. При таком отборе вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отобранных единиц.

При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора.

Так как бесповторный отбор охватывает все новые и новые совокупности, а повторный отбор на всем протяжении одну и ту же совокупность, то бесповторный отбор дает более точные результаты, чем повторный.

По видам отбор делится на индивидуальный, групповой и комбинированный. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности. При групповом отборе в выборочную совокупность отбираются качественно однородные группы или серии изучаемых единиц. При комбинированном отборе происходит сочетание первого и второго вида отбора.

Существует несколько способов отбора:

ü собственно-случайный;

ü механический;

ü типический;

ü серийный;

ü комбинированный.

Собственно-случайный отбор – это отбор, при котором наблюдению подвергается часть совокупности, отобранная из всей совокупности в случайном порядке.

Собственно-случайный отбор бывает повторным и бесповторным. Для собственно-случайного отбора применяются следующие формулы:

Средняя ошибка выборки для средней ( при повторной выборке):

при бесповторной выборке:

Средняя ошибка выборки для доли (при повторной выборке):

при бесповторной выборке:

Численность выборки при определении среднего размера признака (повторная выборка):

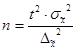
бесповторная выборка:

Численность выборки при определении доли признака (повторная выборка):

бесповторная выборка:

Механический отбор применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (например, номера домов, списки избирателей).

При проведении механического отбора устанавливается шаг отсчета, т.е. расстояние между отбираемыми единицами(N/n – величина обратная доли выборки ) и начало отсчета - номер той единицы, которая должна быть обследована первой.

Механический отбор всегда бывает бесповторным. При этом отборе применяются те же формулы, что и при собственно-случайном бесповторном отборе.

Механический отбор имеет преимущество перед случайным отбором, его не только легче организовать, но при нем единицы выборочной совокупности равномернее распределяются в генеральной совокупности.

Типический отбор представляет собой отбор, при котором генеральная совокупность разбивается на качественно однородные типические группы, затем из каждой группы собственно-случайной или механической выборкой производится отбор единиц в выборочную совокупность.

Из всех типических групп можно отбирать число единиц, пропорциональное их численностям и непропорциональное. В зависимости от этого различают пропорциональный и непропорциональный типический отбор.

Объем выборки из типической группы при отборе пропорциональном численности единиц типических групп определяется по формуле:

где – объем выборки из i -ой типической группы;

– объем i -ой типической группы в генеральной совокупности.

Типический отбор бывает повторным и бесповторным.

Разбивка на типические группы дает возможность избежать влияния межгрупповой вариации на точность выборки. Так как в типическую выборку должны попасть представители всех групп, то средняя ошибка типической выборки зависит только от средней из внутригрупповых дисперсий , а не от общей дисперсии .

При типическом отборе используются следующие формулы:

Средняя ошибка выборки для средней (при повторной выборке):

при бесповторной выборке:

Средняя ошибка выборки для доли (при повторной выборке):

при бесповторной выборке:

Численность выборки при определении среднего размера признака (выборка повторная):

выборка бесповторная:

Численность выборки при определении доли признака (выборка повторная):

выборка бесповторная:

Серийный отбор – это такой отбор, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий обследованию подвергаются все единицы, т.е. применяется сплошное наблюдение.

Поскольку внутри серий обследуются все без исключения единицы, средняя ошибка выборки при отборе равновеликих серий зависит от величины только межгрупповой дисперсии ().