 |
Лабораторная работа №2 Суммарный пуассоновский поток
|
|
|
|
Оглавление
Лабораторная работа №1 Пуассоновский поток. 2
Лабораторная работа №2 Суммарный пуассоновский поток. 6
Лабораторная работа №3 Одноканальная СМО с отказами. 8
Лабораторная работа №4 Одноканальная СМО с ожиданием и ограниченной очередью.. 10
Лабораторная работа №5 Многоканальная СМО с отказами. 14
Лабораторная работа №6 Многоканальная СМО с неограниченной очередью.. 16
Лабораторная работа №7 Многоканальная СМО с ограниченной очередью.. 19
ПРИЛОЖЕНИЕ 1 Таблица значений квантилей 
....... 22
ПРИЛОЖЕНИЕ 2 Таблица значений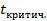 
........... 24
ПРИЛОЖЕНИЕ 3 Алгоритм решения задачи моделирования работы СМО.. 25
Лабораторная работа №1 Пуассоновский поток
Теория.
Система массового обслуживания включает следующие элементы:
- источник требований;
- входящий поток требований;
- очередь;
- обслуживающее устройство (обслуживающий аппарат, канал обслуживания);
- выходящий поток требований.
Под потоком событий в теории вероятностей понимается последовательность событий, происходящих одно за другим в случайные моменты времени. Примерами могут служить: поток вызовов на телефонной станции; поток включений приборов в бытовой электросети; поток заказных писем, поступающих в почтовое отделение; поток сбоев (неисправностей) электронной вычислительной машины; поток выстрелов, направляемых на цель во время обстрела, и т. п. События, образующие поток, в общем случае могут быть различными, но здесь мы будем рассматривать лишь поток однородных событий, различающихся только моментами появления. Такой поток можно изобразить как последовательность точек 
на числовой оси (рисунок 1.1), соответствующих моментам появления событий.
|
|
|
Рисунок 1.1 - Поток событий
Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Такой поток сравнительно редко встречается в реальных системах, но представляет интерес как предельный случай. Типичным для системы массового обслуживания является случайный поток заявок.
Мы рассмотрим потоки событий, обладающие некоторыми особенно простыми свойствами. Для этого введем ряд определений.
1. Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени длиной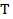 
(рисунок 1.1) зависит только от длины участка и не зависит от того, где именно на оси 
расположен этот участок.
2. Поток событий называется потоком без последействия, если для любых неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.
3. Поток событий называется ординарным, если вероятность попадания на элементарный участок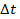 
двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.
Если поток событий обладает всеми тремя свойствами (т. е. стационарен, ординарен и не имеет последействия), то он называется простейшим (или стационарным пуассоновским) потоком. Название «пуассоновский» связано с тем, что при соблюдении условий 1-3 число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона.
Пусть в СМО требования поступают в случайные моменты времени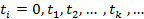 
, так что 
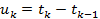(k ≥ 1) – интервалы между поступлениями и, кроме того,
|
(1.1)
Предположим, что случайные величины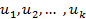 
независимы и имеют показательное распределение с параметром λ:
|
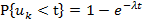
(1.2)
Другими словами, входной поток требований в систему является простейшим.
Пусть ν(t) - число требований, поступивших в СМО в интервале времени (0, t). Тогда справедлива формула
|
|
|
|
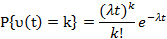
(1.3)
означающая, что если длительности промежутков между поступлениями в систему последовательных требований имеют показательный закон, то случайное число требований, поступивших за время t, имеет распределение Пуассона с параметром 
, а процесс ν(t) является однородным пуассоновским процессом.
Имеет место и обратное: если число требований ν(t), поступивших за время t, является процессом Пуассона с интенсивностью λ, то длительности интервалов uk независимы и имеют одинаковое показательное распределение с параметром λ.
Цель. Смоделировать поток, в котором длительность промежутков времени между поступлениями заявок имеет показательный закон с параметром λ, проверить гипотезу о «пуассоновости» полученного потока СМО.
Входные значения: промежуток наблюдения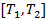 
, параметр λ.
Значения могут быть выбраны в зависимости от номера студента в списке группы I, где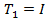 
, 
, 
.
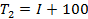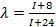Алгоритм решения задачи.
1. Сгенерируем случайное вещественное число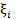 
в диапазоне (0;1). Приведем это число в показательное распределение с помощью формулы:
|
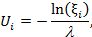
(1.4)
т.к.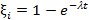 
; где t – промежуток времени, и в нашем случае равный 
(интервал между поступлениями требований).
По формуле (1.1) получаем
|
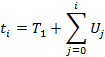
(1.5)
Генерируем массив значени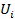й 
и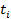 
, пока 
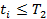. Полученный массив – модель пуассоновского потока.
Необходимо сгенерировать K=50 потоков.
Полученный набор потоков можно изобразить графически в соответствии со следующим рисунком (рисунок 1.2):
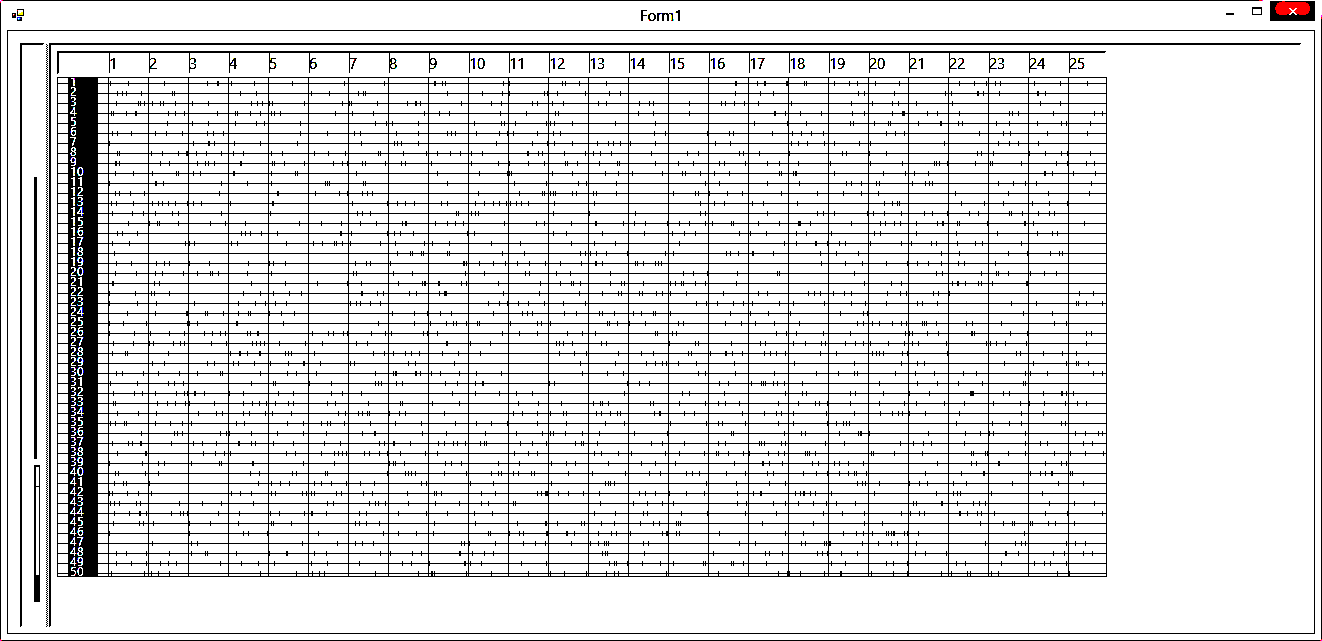
| Номер промежутка |
Рисунок 1.2 Модель пуассоновского потока
2. Разбиваем интервал [T1;T2] на 25 одинаковых промежутков, равных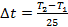 
.
Формируем таблицу следующего вида:
Таблица 1.1 – Сводная таблица модели
(T1, T1+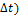 
| (T1+ 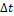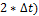 , T1+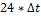 
| (T1+  , T1+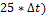 
| ||
| Номер промежутка | 1 | 2 | … | 25 |
| Итер. 1 | X1(1) | X1(2) | … | X1(25) |
| Итер. 2 | X2(1) | X2(2) | .. | X2(25) |
| …. | .. | .. | .. | .. |
| Итер.K | XK(1) | .. | .. | Xk(25) |
Где Xj(i) – количество 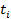в полученном массиве, попавших в промежуток 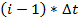(T1+ 
, T1+ 
в потоке j.
3. Из двумерного массива Xj(i) выбрать УНИКАЛЬНЫЕ значения Xj(i) и поместить в массив hl, где l= 
, L-количество уникальных значений Xj(i) в hl или длина массива hl. Составить следующую таблицу:
|
|
|
Таблица 1.2 – Сводная таблица модели
| Параметр | Уникальные значения | |||
| …. | L | |||
| hl | h1 | h2 | ….. | hL |
| nl | n1 | n2 | …. | nL |
| hl* nl | h1* n1 | h2* n2 | …. | hL* nL |
| nlтеоритическоеформула(1.6) | n1теоритическое | n2теоритическое | …. | nLтеоритическое |
|
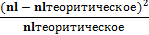
Где nl количество уникальных значений hl в массиве Xj(i).
|
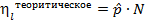
(1.6)
|
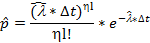
(1.7)
|
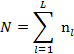
(1.8)
|
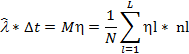
(1.9)
4. Вычислить значение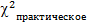 
:
|
(1.10)
5. Вычислить значение квантиля хи-квадрат крит.
Распределение Пирсона c2 (хи - квадрат) – распределение случайной величины
,
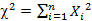где случайные величины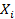 
независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.
Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.
Квантиль хи-квадрат — это число (величина хи-квадрат), при котором функция распределения хи-квадрат равна заданной (затребованной) вероятности ε. Равенство функции распределения хи-квадрат вероятности ε означает, что с вероятностью ε будут наблюдаться значения хи-квадрат, не большие, чем найденный (определенный согласно функции распределения) квантиль хи-квадрат. Таким образом, найти квантиль означает разграничить распределения хи-квадрат согласно заданной вероятности ε.
Для нашей задачи уровень значимости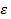 
(вероятность наблюдаемого значения быть случайным отклонением) равен 0,05, а число степеней свободы равно числу карманов с вычетом единицы и числа параметров распознавания (n=25-1-1=23). Значение крит можно найти в приложении 1, а также получить с помощью функции ХИ2ОБР в табличном редакторе MS Excel.
Если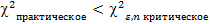 
, то гипотеза о «пуассоновости» потока не отвергается.
6. Сделать вывод о подтверждении или об опровержении гипотезы.
Лабораторная работа №2 Суммарный пуассоновский поток
|
|
|
Теория.
Основным свойством пуассоновского потока, обусловливающим его широкое применение при моделировании, является аддитивность: результирующий поток суммы пуассоновских потоков тоже является пуассоновским с суммарной интенсивностью:
 ,
|
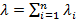(2.1)
где n – число пуассоновских потоков, участвующих в суммировании,
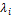– интенсивность i-ого потока.
Предположим, что имеется два точечных процесса и результирующий процесс формируется наложением (суммированием) этих процессов, то результирующий поток соответствует потоку, изображенному на следующем рисунке:
| Поток с интенсивностью l2 |
| Суммарный поток с интенсивностью l=l1+l2 |
Рисунок 2.1 Суммарный поток
Цель. Проверить гипотезу о свойстве аддитивности пуассоновского потока.
Входные значения: промежуток наблюдения 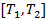, параметр λ.
Значения могут быть выбраны в зависимости от номера студента в списке группы I, где , ,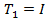 
., 
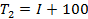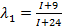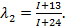
Алгоритм решения.
1. Используя реализацию решения первой лабораторной работы, произведем пункты 1-6 первой лабораторной работы для потока с интенсивностью λ= λ1+ λ2. Данный поток назовем X(t) теор.
2. Выполним пункт 1 первой лабораторной работы для потоков X1(t) с интенсивностью λ1 и X2(t) с интенсивностью λ2. Получим поток X(t) практ= X1(t)+ X2(t), путем объединения массивов ti для каждой выборки двух потоков, как это изображено на рисунке 2.1. Произведем пункты 2-6 первой лабораторной работы для полученного потока.
3. Произведем расчет параметров для каждого из потоков (X(t) практ, X1(t), X2(t), X(t) теор):
- математическое ожидание (формулы (2.2)-(2.4)).
|
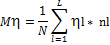
(2.2)
|
(2.3)
|
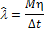
(2.4)
- дисперсию (формула (2.5)).
|
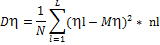
(2.5)
4. Сравним полученные значения:
- 
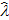и λ для каждого потока;
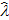- потока X(t)теор, 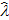потока X(t)практ и 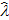, полученного сложением 
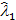потока X1(t) и 
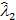потока X2(t).
- сравнить математическое ожидание и дисперсию потоков.
5. Проверить однородность выборок X(t)теор и X(t)практ, т.е. проверить, относятся ли они к общей генеральной совокупности.
В математико-статистических терминах постановка задачи такова: имеются две выборки x1, x2,...,xm и y1, y2,...,yn (т. е. наборы из m и п действительных чисел), требуется проверить их однородность. Можно переформулировать задачу: требуется проверить, есть ли различие между выборками. Если различия нет, то для дальнейшего изучения часто выборки объединяют.
Например, в маркетинге важно выделить сегменты потребительского рынка. Если установлена однородность двух выборок, то возможно объединение сегментов, из которых они взяты, в один. В дальнейшем это позволит осуществлять по отношению к ним одинаковую маркетинговую политику (проводить одни и те же рекламные мероприятия и т.п.). Если же установлено различие, то поведение потребителей в двух сегментах различно, объединять эти сегменты нельзя, и могут понадобиться различные маркетинговые стратегии, своя для каждого из этих сегментов.
|
|
|
Один из методов - критерий Стьюдента, который заключается в следующем:
Пусть есть выборка X (x1,x2……xn) и выборка Y (y1,y2……ym) (в нашем случае m и n равно L соответствующей выборки, взятой из первой лабораторной работы). Найдем математическое ожидание MX и MY и дисперсию DX и DY. Определим статистику Стьюдента t по формуле (2.6).
|
(2.6)
По заданному уровню значимости (пусть равно 0.01) и числу степеней свободы (m+n _ 2) из таблиц распределения Стьюдента находят критическое значение tкр. Если |t|>tкр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t|<tкр, то принимают. Значение tкр можно найти в приложении 2, а также получить с помощью функции СТЬЮДРАСПОБР в табличном редакторе MS Excel.
|
|
|
