 |
Лабораторная работа №3 Одноканальная СМО с отказами
|
|
|
|
Теория.
Простейшей одноканальной моделью с вероятностным входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. Рассмотрим простейшую задачу в теории массового обслуживания – задачу о функционировании одноканальной СМО с отказами.
Пусть система имеет всего один канал обслуживания (s=1) и на нее поступает пуассоновский поток заявок с интенсивностью λ. Заявка, заставшая канал занятым, получает отказ и покидает систему.
Обслуживание заявки продолжается за время обслуживания 
, следовательно «поток обслуживания» простейший с интенсивностью µ. Граф состояний такой системы выглядит следующим образом:
| E0 |
| E1 |
| λ |
| µ |
Рисунок 3.1 Граф состояний СМО < µ | µ | 1 | 0 >
Поток заявок и обслуживания простейшие, т.е. обладающие свойствами стационарности (среднее число событий, воздействующих на систему, в течение единицы времени, остается постоянным), ординарности (вероятность попадания на элементарный участок времени двух и более событий пренебрежимо мала) и отсутствия последействия (для любых непересекающихся участков времени количество событий, попадающих на один из них, не зависит от того, сколько событий попало на другие участки времени).
Система имеет два состояния: E0 - канал свободен и E1 - канал занят. Обозначим вероятности состояний: P0(t) - вероятность состояния E0, P1(t) - вероятность состояния E1. Составим систему уравнений Колмогорова и по условию стационарности прировняем производные нулю:
|
(3.1)
По условию нормировки 
решение системы следующее (см.(1.3)):
|
|
|
|
(3.2)
|
(3.3)
Для 1-канальной СМО с отказами вероятность P0(t) есть не что иное, как относительная пропускная способность системы q:
|
(3.4)
По истечении большого интервала времени (при t 
∞) достигается стационарный режим:
|
(3.5)
Абсолютная пропускная способность (А) - среднее число заявок, которое может обслужить СМО в единицу времени:
|
(3.6)
Вероятность отказа в обслуживании заявки будет равна вероятности состояния E1:
|
(3.7)
Данная величина может быть интерпретирована как средняя доля необслуженных заявок среди поданных.
Цель. Исследование одноканальной СМО с отказами и ее свойства стационарности.
Входные значения: параметр λ из первой лабораторной работы, время обслуживания 
.
Значения могут быть выбраны в зависимости от номера студента в списке группы N, 
где l=0,3 для N-нечетное и l=0,4 для N-четное.
Алгоритм решения.
1. Определим интенсивность выходного потока по формуле (3.8).
|
(3.8)
2. Построим следующую таблицу, получая значения P0(t) и P1(t) по формулам (3.2) и (3.3), пока не выполниться условие 
и 
, где 
.
Таблица 3.1 – Сводная таблица результатов
| t | P0(t) | P1(t) |
| t1=0 | (3.2) | (3.3) |
t2= t1 +  , где 
| ||
| ….. | ||
| tn= tn-1 +
|
Сравните полученные конечные значения P0(t) и значение P0(t), полученное по формуле (3.5). Сделайте выводы.
Лабораторная работа №4 Одноканальная СМО с ожиданием и ограниченной очередью
Теория.
Рассмотрим теперь одноканальную СМО с ожиданием. Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание поток имеет интенсивность λ. Интенсивность потока обслуживания равна μ (т. е. в среднем непрерывно занятый канал будет выдавать μ обслуженных заявок). Длительность обслуживания — случайная величина, подчиненная показательному закону распределения. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
|
|
|
Рассмотрим систему с ограниченной очередью. Предположим, что независимо оттого, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N-требований (заявок), из которых одна обслуживается, а (N-1) ожидают в очереди длиной m (m=N-1).
Клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте и такие заявки теряются. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.
Граф состояний такой системы выглядит следующим образом:
| E0 |
| λ |
| µ |
| E1 |
| E2 |
| Ek |
| Em+1 |
| λ |
| λ |
| λ |
| λ |
| λ |
| µ |
| µ |
| µ |
| µ |
| µ |
| … |
| … |
| … |
| … |
Рисунок 4.1 Граф состояний СМО < µ | µ | 1 | m >
Обозначим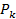 
- вероятность того, что в системе находится k заявок, т.е. система находится в состоянии 
.
|
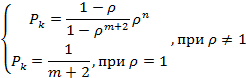
(4.1)
Параметр 
- приведенная интенсивность потока, и он находится по формуле (4.2).
|
(4.2)
Тогда вероятность того, что канал обслуживания свободен и в системе нет ни одного, клиента высчитывается по формуле
|
(4.3)
По формуле (4.1) можно высчитать вероятность отказа, т.е. вероятность того, что канал занят и вся очередь наполнена:
|
(4.4)
Относительная пропускная способность системы q будет являться противоположным событием событию «отказа заявки на обслуживание», и высчитывается по формуле.
|
(4.5)
Абсолютная пропускная способность (А) - среднее число заявок, которое может обслужить СМО в единицу времени:
|
(4.6)
Среднее число находящихся в очереди заявок:
|
(4.7)
Среднее время пребывания заявки в очереди:
|
(4.8)
|
|
|
