Цель. Исследование одноканальной СМО с ожиданием и ограниченной очередью.

Входные значения: параметр λ из первой лабораторной работы, время обслуживания .

 

Значения могут быть выбраны в зависимости от номера студента в списке группы N, где l=0,1,3 для N-нечетное и l=0,2,4 для N-четное.

 

Алгоритм решения.

 

1. Построить следующую таблицу, используя формулы указанные в таблице.

 

m

l

tобсл

Pотк.теор

A

q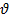

Pобсл

Pотказ.прак.

l1

tобсл(l1)

(4.2)

(4.4)

(4.6)

(4.5)

(4.7)

(4.8)

(1’)

(2’)

(3’)

(4’)

l2

tобсл(l2)

l3

tобсл(l3)

l1

tобсл(l1)

l2

tобсл(l2)

l3

tобсл(l3)

l1

tобсл(l1)

l2

tобсл(l2)

l3

tобсл(l3)

 

2. Для расчета 1’-2’ необходимо смоделировать два пуассоновских потока с интенсивностью и , как это делалось в лабораторной работе №2, и вычитать соответствующие значения по формуле (2.4).

3. Для расчета 3’-4’ необходимо провести следующее моделирование. Для каждого потока из 50 смоделированных в пункте 2 потоков с интенсивностью и каждого соответствующего значения m_i и t_обсл(l_j) построить график, содержащий следующие оси:

a) входящие в СМО заявки, представленные массивом t_i, который берется из соответствующего потока;

b) время вхождения заявки в очередь;

c) время отправления заявки на выполнение;

d) время выхода выполненной заявки из СМО;

e) время выхода заявки с отказом.

Данный график можно представить следующим образом:

e)

a)

b)

c)

d)

t

Рисунок 4.2 Моделирование работы СМО с длиной очереди m=2 и временем обслуживания t_обсл

По результатам моделирования необходимо посчитать вероятность событий «заявка обслужена» и «заявка получила отказ от обслуживания», полученную в результате испытаний по формуле (4.9). Изобразить работу модели графически в соответствии с рисунком 4.2.

(4.9)

 

 

где - вероятность наступления события A;

- число благоприятных A событий при испытаниях;

– общее число испытаний.

 

Возможный алгоритм моделирования работы СМО представлен в приложении 3.

 

4. Рисуем график функций P_{отк.модельн.}(t_обсл) и P_{обсл.теорит.}(t_обсл) для каждого m_i, где по абрисе будет 3 отметки t_обсл(l₁), t_обсл(l₁), t_обсл(l₁), а по ординате значения P_{отк.модельн.} и P_{обсл.теорит.}(t_обсл) для каждого m_i (всего 6 кривых).

 

5. Создаем таблицу для решения оптимизационной задачи.

 

				Доход на ед.времени	Расход на ед. временни	Прибыль
	Pотказа		tобсл	Доход от заявки	Число обсл. заявок	Общ. доход	Расходы на 1 прибор	Расходы на содерж.места в очереди	Число мест в очереди	Общ расход
			tобсл1	S1+=100	A	= A * S1+	Sприб-=10	S1-=1	m1	=m* S1-+ Sприб-	=(*1)-(*2)
			tобсл2			(*1)			m1	(*2)
			tобсл3						m1
			tобсл1						m2
			tобсл2						m2
			tобсл3						m2
			tобсл1						m3
			tобсл2						m3
			tобсл3						m3

 

6. В результате полученной в пункте 5 таблицы нарисовать график зависимости прибыли от числа мест в очереди. Сделать выводы.

 

Лабораторная работа №5 Многоканальная СМО с отказами

Теория.

Рассмотрим многоканальную СМО с отказами. Система массового обслуживания имеет S каналов. Входящий поток заявок на обслуживание имеет интенсивность λ. Заявка, поступившая в момент, когда все каналы заняты, получает отказ на обслуживание.

Граф состояний такой системы выглядит следующим образом:

E0

λ

µ

E1

E2

Ek

Es

λ

λ

λ

λ

λ

2µ

3µ

kµ

(k+1)µ

sµ

…

…

…

…

Рисунок 5.1 Граф состояний СМО < µ | µ | S | 0 >

Слева направо переходит один и тот же поток – входящий поток с интенсивностью λ. Если занято k-каналов и приходит новая заявка, система переходит в состояние E_k+1.

Справа налево поток из состояния E_k с интенсивностью kµ переходит в состояние E_k-1.

Пользуясь общими правилами можно составить уравнения Колмогорова для вероятностей состояний:

 

(5.1)

 

Параметр - приведенная интенсивность потока, и он находится по формуле (5.2).

(5.2)

 

 

Решив систему (5.1) и подставив (5.2), получим формулу (5.3).

(5.3)

 

 

По условию нормировки получим формулу (5.4).

(5.4)

 

Заявка получает отказ, если все S каналов заняты, тогда вероятность отказа – это вероятность состояния E_s:

(5.5)

 

 

Вероятность (q) того, что заявка будет принята к обслуживанию, дополняет до единицы:

(5.6)

 

Абсолютная пропускная способность (А) - среднее число заявок, которое может обслужить СМО в единицу времени:

(5.7)

 

Среднее число занятых каналов будет находиться по формуле (5.8).

(5.8)

 

Цель. Решить оптимизационную задачу на примере СМО < µ | µ | S | 0 >.

Входные значения: параметр λ, время обслуживания из четвертой лабораторной работы.

 

Значения необходимо выбрать такие, чтобы .

 

Задача. Определить оптимальное число контролёров ОТК, которые производят проверку выпускаемого оборудования. Если контролера нет на месте, оборудование отправляется без проверки. На каждое оборудование, не прошедшее проверку, накладывается штраф. На содержание одного рабочего места необходимо 500$/год. Заработная плата контролёра ОТК составляет 7500$/год. Контролёр получает зарплату по времени, а не по факту выработки. Штраф за отказ от обслуживания составляет 4$ за один отказ. Годовой фонд времени составляет 6000 часов. Размерность интенсивностей входного и выходного потоков шт/час.

 

Алгоритм решения.

 

1. Формула для расчета затрат:

(5.9)

 

где – затраты на работу s-каналов;

- коэффициент эффективности капиталовложения (0,15$/год);

- затраты на рабочее место (500$/год);

- затраты на заработную плату контролёра ОТК (7500$/год);

– затраты на простой контролёра ОТК (7500$/год);

– затраты на отказ от обслуживания (4$/шт.);

– среднее число занятых каналов ();

–годовой фонд рабочего времени (6000 часов);

 

2. Протабулировать функцию (5.9) при ;

 

3. Построить график зависимости затрат от числа обслуживающих каналов, и найти оптимальное число обслуживающих каналов для данной задачи.

 

Не забывайте проверять условие существования стационарного режима для текущей итерации.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: