 |
Лабораторная работа №6 Многоканальная СМО с неограниченной очередью
|
|
|
|
Теория.
Пусть дана система, имеющая S каналов обслуживания, на которые поступает простейший поток требований интенсивностью λ. Пусть поток обслуживания также простейший и имеет интенсивность μ(для одного канала). Очередь на обслуживание не ограничена.
Граф состояний такой системы выглядит следующим образом:
| E0 |
| λ |
| µ |
| E1 |
| Es |
| Es+m |
| λ |
| λ |
| λ |
| λ |
| 2µ |
| sµ |
| sµ |
| sµ |
| Ek |
| λ |
| λ |
| kµ |
| (k+1)µ |
| очереди нет |
| λ |
| sµ |
| … |
| … |
| … |
| … |
| … |
| … |
| … |
| … |
Рисунок 6.1 Граф состояний СМО < µ | µ | S | ∞ >
Интенсивность потока обслуживаний меняется в зависимости от состояния системы: kμ при переходе из состояния Ek в состояние Ek-1, так как может освободиться любой из k-каналов; после того, как все каналы заняты обслуживанием, интенсивность потока обслуживаний остается равной sμ, при поступлении в систему следующих заявок.
Составив уравнения Колмогорова, прировняв их нулю, решив данную систему и преобразовав решения с помощью условия нормировки и формул геометрической прогрессии, получим формулы (7.1)-(7.2).

|
(6.1)

|
(6.2)
По формуле (6.1) можно высчитать вероятность ожидания, т.е. вероятность того, что заявка попадет в очередь:

|
(6.3)
Среднее число занятых каналов будет находиться по формуле (6.4).

|
(6.4)
Среднее число находящихся в очереди заявок:

|
(6.5)
Среднее время пребывания заявки в очереди:

|
(6.6)
Среднее число заявок в СМО:

|
(6.7)
Среднее время пребывания заявки в СМО:

|
(6.8)
Цель. Решить оптимизационную задачу на примере СМО < µ | µ | S | ∞ >.
Входные значения: параметр λ=0,5 барж/сутки, µ=0,5 барж/сутки.
|
|
|
Задача. Определить оптимальное число причалов промышленного речного порта, принимающих биржи с сыпучим материалом. Поток поступающих бирж простейший с интенсивностью 0,5 барж/сутки. Время разгрузки баржи имеет показательный закон с параметром 0,5 барж/сутки. Цена оборудования одного причала 100000$. Текущие затраты на содержание одного причала 400$/сутки при его использовании и 200$/сутки при его простое. Затраты на содержание баржи, ожидающей разгрузки, составляет 1000$/сутки, если время ожидания меньше 2 суток, и 1600$/сутки, если время ожидания больше 2 суток.
Алгоритм решения.
1. Формула для расчета затрат:

|
(6.9)
где  – затраты на работу порта;
– затраты на работу порта;
 - коэффициент эффективности капиталовложения (0,15$/год);
- коэффициент эффективности капиталовложения (0,15$/год);
 - цена оборудования одного причала (100000$);
- цена оборудования одного причала (100000$);
 - текущие затраты на содержание причала (400$/сутки);
- текущие затраты на содержание причала (400$/сутки);
 – текущие затраты на содержание причала в простое (200$/сутки);
– текущие затраты на содержание причала в простое (200$/сутки);
 – затраты на содержание баржи, ожидающей разгрузки;
– затраты на содержание баржи, ожидающей разгрузки;
 – средняя длина очереди (
– средняя длина очереди (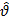 );
);
 –среднее число занятых приборов (
–среднее число занятых приборов ( );
);
 –годовой фонд рабочего времени (365 суток).
–годовой фонд рабочего времени (365 суток).

|
(6.10)
где  - затраты на содержание баржи, ожидающей разгрузки менее
- затраты на содержание баржи, ожидающей разгрузки менее  (1000$/сут.);
(1000$/сут.);
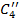 - затраты на содержание баржи, ожидающей разгрузки более
- затраты на содержание баржи, ожидающей разгрузки более  (1600$/сутки);
(1600$/сутки);
 – время ожидания баржой разгрузки;
– время ожидания баржой разгрузки;
 – время ожидания, после которого стоимость содержания баржи в ожидании увеличивается (2 суток).
– время ожидания, после которого стоимость содержания баржи в ожидании увеличивается (2 суток).
Вероятность ожидания менее t суток высчитывается по формуле (6.11).

|
(6.11)
Событие «баржа ожидает более t суток» является противоположным событием событию «баржа ожидает менее t суток».
2. Протабулировать функцию (6.10) при  ;
;
3. Построить график зависимости затрат от числа обслуживающих каналов, и найти оптимальное число обслуживающих каналов  для данной задачи.
для данной задачи.
4. Протабулировать функцию (6.10) при  =
=  , зафиксировав в данной формуле
, зафиксировав в данной формуле 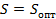 .
.
5. Построить график зависимости затрат от времени ожидания, после которого накладывается штраф на содержания баржи в ожидании.
|
|
|
6. Протабулировать функцию (6.10) при  =
=  с произвольным шагом, зафиксировав в данной формуле
с произвольным шагом, зафиксировав в данной формуле 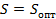 и
и  . Построить график данной зависимости.
. Построить график данной зависимости.
7. Протабулировать функцию (6.10) при 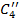 =
=  с произвольным шагом, зафиксировав в данной формуле
с произвольным шагом, зафиксировав в данной формуле 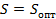 ,
, 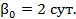 и
и  . Построить график данной зависимости.
. Построить график данной зависимости.
Не забывайте проверять условие существования стационарного режима для текущей итерации и единицы измерения.
|
|
|


