 |
1) Частотне представлення сигналів.
|
|
|
|
1) Частотне представлення сигналів.
А. Залежність амплітуди складового сигналу, зокрема гармонік, від частоти називається амплітудно-частотним спектром (АЧС), а фази від частоти – фазочастотним спектром (ФЧС).
Періодичний сигнал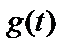 
, має період 
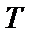, частоту повторення 
, рівну 
, і в загальному випадку нескінченний спектр, що описується ряд Фур'є:
. (6а)
Представлення сигналу 
рядом Фур'є прийнято називати спектральним або гармонійниманалізом цього сигналу.
Перший доданок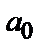 
виразу являє собою постійну складового сигналу, фактично постійний струм, що може бути дорівнює нулеві (тобто бути відсутнім). Тут пари доданків 
і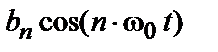 
з однаковою частотою 
, кратній основній частоті ( fundamental frequency ) 
, є гармоніками з амплітудою 
і початковою (обумовленою в момент часу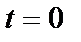 
) фазою 
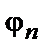, що обчислюються по співвідношеннях
, 
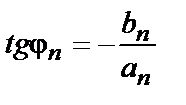. (7)
У такий спосіб (6) можна переписати у виді нескінченної суми гармонік (як правило косинусоідальних):
. (8)
Кожна з таких гармонік може бути представлена на комплексній площині одиночним обертовим
| an |
| Im |
Рис. 5. Графічне представлення 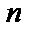 -й гармоніки (доданка в (6а) )
|
| Re |
| bn |
|
| p/2 |
| p |
| 3p/2 |
| jn |
| n× w0 |
і кутовою швидкістю, що пропорційна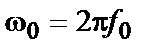 
рад / с,
Таким чином, спектри різних періодичних сигналів відрізняються друг від друга лише значеннями коефіцієнтів Фур'є 
й 
у (6а), які можна розрахувати по формулах Ейлера – Фур’є
, 
, 
(6б)
Коефіцієнт 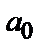має сенс середнього значення сигналу за період.
|
|
|
Вирішуючи задачу розкладання в ряд Фур'є періодичної функції при розрахунку коефіцієнтів Фур'є ( і ) для мінімізації розрахунків варто враховувати її специфіку. Так якщо остання являє собою парну функцію, для якої справедлива рівність 
, відомо, що ряд Фур'є такої функції містить тільки косинусоідальні складові спектра. Причому постійна складова парної функції може бути як дорівнює нулеві, так і відмінна від нього.
Для непарних функцій справедливе рівність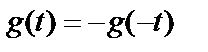 
, тобто функції симетричні відносно початку координат, виконується правило, згідно якого їхній спектр не має косинусоідальних складових, а постійна складова дорівнює нулеві.
Для ще одного виду симетрії, називаної псевдосиметрією, для якої власне симетрія відсутня, але з'являється інверсія напівперіодів, що чергуються, характерним є відсутність парних гармонік і постійної складової сигналу. При цьому в наявних доданках ряду присутні як синусоідальні, так і косинусоідальні складового сигналу.
2) Методи цифрового кодування.
При цифровому кодуванні дискретної інформації застосовують потенційні й імпульсні коди.
У потенційнихкодах для представлення логічних одиниць і нулів використовується тільки значення потенціалу сигналу, а його перепади, що формують закінчені імпульси, в увагу не приймаються. Імпульснікоди дозволяють представити двійкові дані або імпульсами визначеної полярності, або частиною імпульсу — перепадом потенціалу визначеного напрямку.
2. 1. Потенційні коди
Потенційний код без повернення до нуля (NRZ)
На рис. 4, а (увага, на цьому рисунку переплутані полярності сигналу) ілюструється метод потенційного кодування без повернення до нуля (Non Return to Zero, NRZ ). Остання назва відображає ту обставину, що при передачі послідовності одиниць сигнал не повертається до нуля протягом такту (в інших методах кодування повернення до нуля в цьому випадку відбувається). Метод NRZ простий у реалізації, володіє гарної розпізнаваністю помилок (через двох різко відрізняються потенціалів), але не має властивості самосинхронізації. При передачі довгої послідовності одиниць або нулів сигнал на лінії не змінюється, тому приймач позбавлений можливості визначати по вхідному сигналу моменти часу, коли потрібно в черговий раз зчитувати дані. Навіть при наявності високоточного тактового генератора приймач може помилитися з моментом знімання даних, тому що частоти двох генераторів ніколи не бувають повністю ідентичними. Тому при високих швидкостях обміну даними і довгими послідовностями одиниць або нулів невелика неузгодженість тактових частот може привести до помилки в цілий такт і, відповідно, зчитуванню некоректного значення біта.
|
|
|
|
|
|
