 |
1) Квантування повідомлень. 2) Часове представлення сигналів.
|
|
|
|
1) Квантування повідомлень
Квантуванням повідомлень (сигналів) називається представлення безперервних повідомлень (сигналів) у виді послідовності їхніх дискретних значень. Розрізняють квантування (дискретизацію) за часом, за рівнем і комбіноване квантування.
Заміна безперервної шкали рівнів дискретної називається квантуванням за рівнем.
У техніці зв'язку знаходять застосування два методи квантування за рівнем. При першому методі незалежно квантують кожну координату дискретного представлення безперервного процесу. В другому методі квантуванню піддають різницю 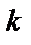 -ї координати дискретного представлення і значення цієї координати, передбачену по попереднім
-ї координати дискретного представлення і значення цієї координати, передбачену по попереднім  координатам, або значення (
координатам, або значення ( 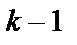 )-ї координати.
)-ї координати.
Перший з цих методів звичайно називають імпульсно-кодовою модуляцією, а другий — дельта-модуляцією. Обидва ці терміни є устояними, однак ніякого відношення до власне модуляції не мають. Нижче основну увагу приділимо імпульсно-кодовій модуляції (ІКМ) (Pulse Amplitude Modulation, РАМ), що представляє собою різновид комбінованого квантування і знайшла широке застосування в цифровій телефонії.
Фактичне значення функції замінюється найближчим рівнем квантування. Погрішність у передачі рівня, що виникає за рахунок цього, називається шумом квантування. Часова діаграма різниці між квантованими і фактичними значеннями являє собою послідовність імпульсів, полярність яких відповідає знакові помилки квантування  , причому
, причому 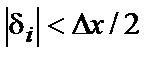 (рис. 2. 9б).
(рис. 2. 9б).
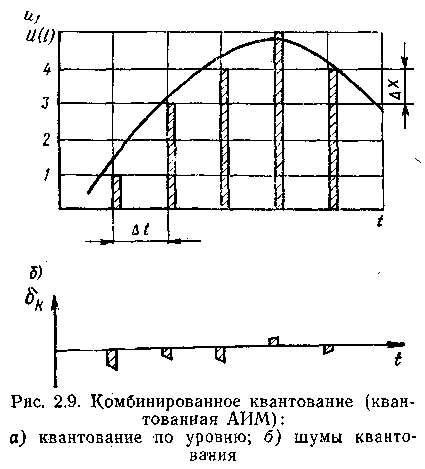
Якщо прийняти, що всі значення безперервної функції в межах кроку квантування  рівноімовірні, то середньоквадратична помилка квантування
рівноімовірні, то середньоквадратична помилка квантування  пов'язана з кроком квантування співвідношенням
пов'язана з кроком квантування співвідношенням
|
|
|
 . (4)
. (4)
Таким чином, середньоквадратична погрішність 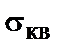 зменшується зі зменшенням кроку квантування. Однак по мірі зменшення
зменшується зі зменшенням кроку квантування. Однак по мірі зменшення  зростає імовірність того, що під впливом перешкод рівень сумарного сигналу (з урахуванням перешкод) виявиться ближчим до іншого рівня квантування, ніж до переданого.
зростає імовірність того, що під впливом перешкод рівень сумарного сигналу (з урахуванням перешкод) виявиться ближчим до іншого рівня квантування, ніж до переданого.
Крок квантування за рівнем (  ) вибирається таким чином, щоб погіршення точності виміру дискретизуємої функції не перевищувало деякого заданого значення, у якості якого зазвичай вибирають
) вибирається таким чином, щоб погіршення точності виміру дискретизуємої функції не перевищувало деякого заданого значення, у якості якого зазвичай вибирають
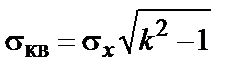 ,
,
де  – коефіцієнт, що визначає припустиме збільшення середньоквадратичної помилки виміру дискретизуємої функції за рахунок квантування;
– коефіцієнт, що визначає припустиме збільшення середньоквадратичної помилки виміру дискретизуємої функції за рахунок квантування;
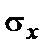 — середньоквадратична помилка виміру функції, обумовлена точністю вимірювальної системи. Знаючи середньоквадратичну помилку виміру функції
— середньоквадратична помилка виміру функції, обумовлена точністю вимірювальної системи. Знаючи середньоквадратичну помилку виміру функції 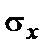 і задаючись припустимим коефіцієнтом
і задаючись припустимим коефіцієнтом 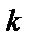 , крок квантування
, крок квантування  в (4) визначається зі співвідношення
в (4) визначається зі співвідношення
 , (5)
, (5)
а число можливих рівнів 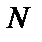 , що може приймати передана функція, яка має діапазон зміни
, що може приймати передана функція, яка має діапазон зміни  , визначається співвідношенням
, визначається співвідношенням 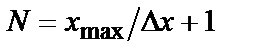 . При наявності шумів квантування
. При наявності шумів квантування 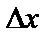 може вибиратися виходячи з припустимої імовірності прийому з помилкою даного рівня.
може вибиратися виходячи з припустимої імовірності прийому з помилкою даного рівня.
Число розрядів 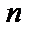 , необхідне для передачі в двійковому коді всіх можливих значень функції, визначається співвідношенням
, необхідне для передачі в двійковому коді всіх можливих значень функції, визначається співвідношенням  .
.
2) Часове представлення сигналів.
На рис. 2 приведена епюра напруги періодичного відеоімпульсу. Розглянемо на його прикладі основні часові параметри сигналів.
| f0 |
| tu |
| t |
| Рис. 2. |
| u(t) |
| U0 |
| 0. 9 U0 |
| 0. 5 U0 |
| 0. 1 U0 |
| T=1/F |
| tф1 |
| tф2 |
До часових параметрів сигналу (імпульсу) відносяться його амплітуда 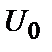 і тривалість
і тривалість  (звичайно виміряється на рівні
(звичайно виміряється на рівні 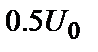 (частіше
(частіше 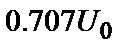 , а рівень 0. 5 – для випадку
, а рівень 0. 5 – для випадку 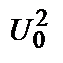 , тобто потужності), а для періодичної послідовності імпульсів – додатково період
, тобто потужності), а для періодичної послідовності імпульсів – додатково період 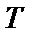 і шпаруватість
і шпаруватість 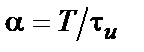 (для періодичної послідовності прямокутних імпульсів). Імпульс також характеризується переднім (
(для періодичної послідовності прямокутних імпульсів). Імпульс також характеризується переднім ( 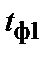 , вимірюється між рівнями
, вимірюється між рівнями 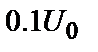 і
і 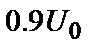 сигналу) і заднім фронтом (
сигналу) і заднім фронтом (  , вимірюється між рівнями
, вимірюється між рівнями 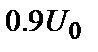 і
і  сигналу) (див. ДСТ).
сигналу) (див. ДСТ).
|
|
|
Стосовно до цифрових інформаційних послідовностей прямокутних імпульсів, що кодують, наприклад, для двійкові значення «0» і «1», оцінюють кількість одиничних елементів 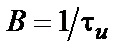 , переданих в одиницю часу. Ця величина називається швидкістю маніпуляції і має розмірність Бод. *)
, переданих в одиницю часу. Ця величина називається швидкістю маніпуляції і має розмірність Бод. *)
Швидкість маніпуляції і частота періодичної послідовності зі шпаруватістю  зв'язані співвідношенням
зв'язані співвідношенням
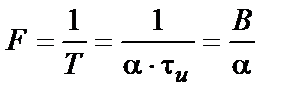 , Гц.
, Гц.
Швидкість передачі інформації визначається кількістю інформації  (біт), переданих в одиницю часу. Для багатопозиційних рівноімовірних сигналів з числом значущих позицій рівним
(біт), переданих в одиницю часу. Для багатопозиційних рівноімовірних сигналів з числом значущих позицій рівним  імовірність появи
імовірність появи 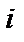 -го сигналу дорівнює
-го сигналу дорівнює 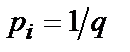 . Тоді інформаційна швидкість дорівнює
. Тоді інформаційна швидкість дорівнює
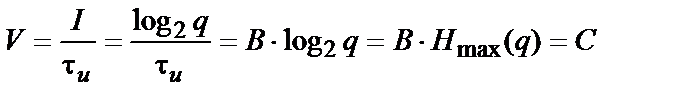 .
.
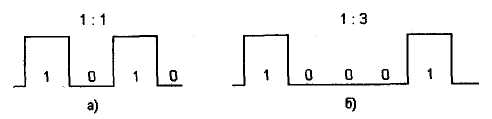 Рис. 3. Примеры периодических последовательностей
Рис. 3. Примеры периодических последовательностей
|
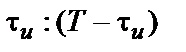 або в нормованій формі
або в нормованій формі 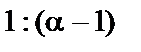 . На рис. 3 і показані послідовності типу «точки» (меандр) 1: 1 (а) і сигнали виду 1: 3 (б).
. На рис. 3 і показані послідовності типу «точки» (меандр) 1: 1 (а) і сигнали виду 1: 3 (б).
Помітимо, що ряд «часових» параметрів характерний для конкретних різновидів сигналів. Так найважливішою характеристикою радіоімпульсів є несуча частота 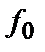 або період
або період 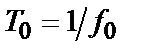 гармонійного коливання. А при використанні складних (складених) сигналів додатково задається тривалість
гармонійного коливання. А при використанні складних (складених) сигналів додатково задається тривалість  парциальних сигналів (парциала або чипа), а також їхня кількість
парциальних сигналів (парциала або чипа), а також їхня кількість 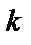 у сигналі, таке що
у сигналі, таке що 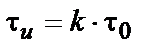 .
.
Перейдемо до математичного опису сигналів. В інформаційних радіоелектронних системах найбільше поширення одержали сигнали на основі радіоімпульсів і їхніх послідовностей.
Сигнали, застосовувані в радіоканалах зв'язку і бездротових мережах, у загальному випадку можна записати у виді високочастотного ( 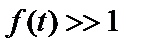 ) коливання (у літературі найбільше часто такі коливання представляються косинусом-гармонікою)
) коливання (у літературі найбільше часто такі коливання представляються косинусом-гармонікою)
 . (2)
. (2)
Тут 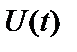 – амплітуда сигналу, що змінюється в часі,
– амплітуда сигналу, що змінюється в часі, 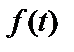 - частота коливання (
- частота коливання ( 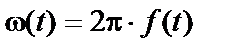 - кутова частота),
- кутова частота), 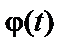 – його початкова фаза. Частоту
– його початкова фаза. Частоту 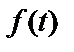 (
(  ) часто називають «несучою», тому що в більшості випадків вона «несе» інформацію, що міститься в сигналі, що модулює, у своїй амплітуді (амплітудна модуляція), частоті (частотна модуляція) або фазі (фазова модуляція). Величину
) часто називають «несучою», тому що в більшості випадків вона «несе» інформацію, що міститься в сигналі, що модулює, у своїй амплітуді (амплітудна модуляція), частоті (частотна модуляція) або фазі (фазова модуляція). Величину  називають миттєвою фазою сигналу.
називають миттєвою фазою сигналу.
|
|
|
| u(t) |
| t |
| U0 |
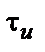
|
| Рис. 4. |
| T0 |
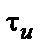 з постійними амплітудою
з постійними амплітудою 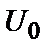 , частотою
, частотою 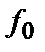 і початковою фазою
і початковою фазою 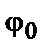 , його можна описати співвідношенням:
, його можна описати співвідношенням:
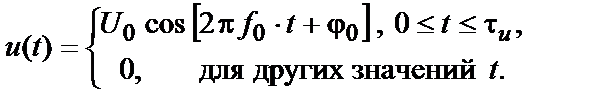 (3)
(3)
Епюра напруги (графік залежності напруги від часу) сигналу (3) при 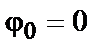 представлена на рис. 4.
представлена на рис. 4.
Відмінною рисою сигналу виду (2) є повільна зміна як амплітуди 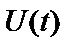 , так і фази
, так і фази  за період (
за період ( 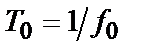 ) коливання. У граничному випадку (при нескінченній тривалості імпульсу (
) коливання. У граничному випадку (при нескінченній тривалості імпульсу (  ) постійної амплітуди
) постійної амплітуди 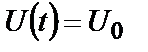 і початкової фази
і початкової фази  ) приходимо до гармонійного коливання.
) приходимо до гармонійного коливання.
Моделі сигналів (2) і (3) представлені в дійсній формі. Використовуючи формули Ейлера
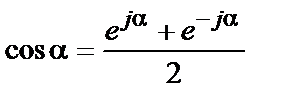 ,
, 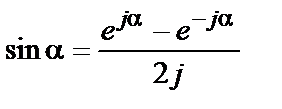 ,
, 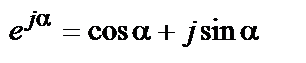 (3*)
(3*)
вираз (3) представимо у виді:
 , (4)
, (4)
де  – комплексна амплітуда сигналу, а комплексна гармоніка в цілому записується у виді
– комплексна амплітуда сигналу, а комплексна гармоніка в цілому записується у виді
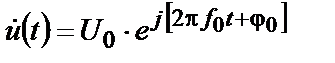 ,
,
тобто дійсному сигналові 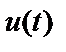 відповідає реальна частина сигналу, записаного в комплексній формі.
відповідає реальна частина сигналу, записаного в комплексній формі.
Інша форма комплексного запису сигналу (3) також заснована на (3*) і має вигляд:
 , (5)
, (5)
де 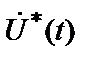 – сполучене значення комплексної амплітуди
– сполучене значення комплексної амплітуди 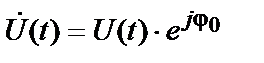 виду
виду
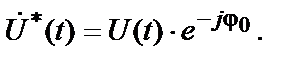
Таким чином, будь-яке високочастотне коливання 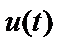 може бути зведено або до реальної частини добутку комплексної амплітуди
може бути зведено або до реальної частини добутку комплексної амплітуди 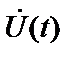 і високочастотного комплексного множника
і високочастотного комплексного множника 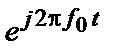 , або до напівсуми аналогічних комплексно-сполучених добутків.
, або до напівсуми аналогічних комплексно-сполучених добутків.
Білет №13
1. Загальна характеристика методів підвищення вірності передачі інформації
2. Методи фазової модуляції і маніпуляції
Відповіді
|
|
|


