 |
Тема 2. Исследование нелинейных функций и построение их графиков
|
|
|
|
Постановка задачи
Задача исследования функций y=f(x) и построение графиков функций с применением производной является одной из главных задач дифференциального исчисления. Общая схема исследования функции и построение ее графика включает следующие действия.
1..Исследование функции на возрастание (неубывание) или убывание (невозрастание)
2. Исследование экстремумов функции; нахождение координат максимума и минимума функции.
3. Исследование функции на выпуклость вверх или вниз. Нахождение точки перегиба функции
4. Создание графического отображения рядов аргумента, функции, ее первой и второй производных, и отложение характерных точек (пп. 6‑8) на графике функции.
Данные исследования области определения и отделения критических точек функции (см. Тема 1, алгоритмы 1.1, 2.1-2.4) приведены на электронной таблице (рис. 1.1) и встроенной диаграмме (рис.1.2).
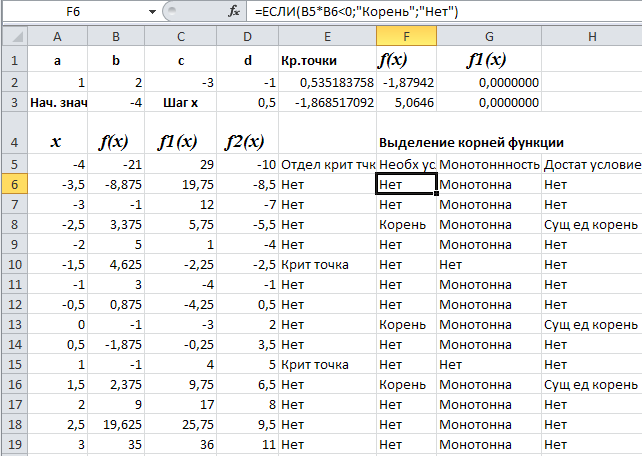
Рис. 1.1. Электронная таблица для вычисления рядов значений величин x, f(x), f1(x) и, f2(x) для функции вида f(x)=ax3+bx2+cx+d
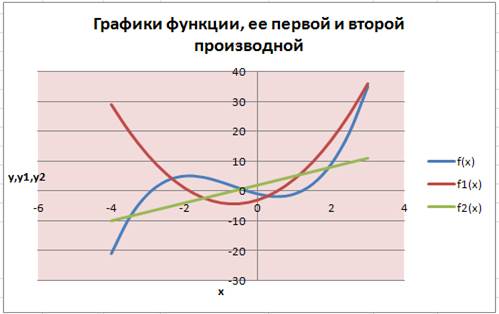
Рис. 1.2.
2. Исследование функции на возрастание (неубывание) или убывание (невозрастание)
Алгоритм 2.1. Исследование функции на возрастание (неубывание) или убывание (невозрастание )
Для исследования функции f(x) на интервале [ a,b ] на возрастание (неубывание) или убывание (невозрастание ) аналитическим способом необходимо воспользоваться определениями и теоремами которые даны в математическом анализе «О возрастающей функции f(x) на интервале [ a,b ]» и «Об убывающей функции f(x) на интервале [ a,b ] ».
Определение 1. Функция f(x) называется возрастающей на интервале [ a,b ], если при возрастании аргумента x (при x2> x1)в этом интервале соответствующие значения функции f(x) также возрастают, иначе функция называется невозрастающей. Логическое условие, которое имеет значение ИСТИНА, когда выполняется условие возрастания функции на интервале [ a,b ], имеет вид (1)
|
|
|
f(x2) > f(x1) (1)
Теорема 1. Функция f(x) называется возрастающей на интервале [ a,b ], если в любой точке x, расположенной на интервале [ a,b ], функция имеет неотрицательную производную. Логическое условие, которое имеет значение ИСТИНА, когда выполняется условие возрастания функции на интервале [ a,b ], имеет вид (2)
f1(x) >=0. (2)
Определение 2. Функция f(x) называется убывающей на интервале [ a,b ], если при возрастании аргумента x (при x2>x1)в этом интервале соответствующие значения функции f(x) убывают, иначе функция называется неубывающей. Логическое условие, которое имеет значение ИСТИНА, когда выполняется условие убывания функции на интервале [ a,b ], имеет вид (3)
f(x2) < f(x1). (3)
Теорема 2. Функция f(x) называется убывающей на интервале [ a,b ], если в любой точке x, расположенной на интервале [ a,b ], функция имеет неположительную производную. Логическое условие, которое имеет значение ИСТИНА, когда выполняется условие убывания функции на интервале [ a,b ], имеет вид (4)
f1(x) <=0. (4)
1. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение условие возрастания функции (1) с помощью логической функции ЕСЛИ(). Если логическое условие (1) имеет значение ИСТИНА, вывести текст «Возрастающая», иначе «Невозрастающая». Провести анализ результатов выполнения условия возрастания функции на этих интервалах.
2. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение условие неубывания функции, которое является отрицанием условия убывания (3),
(НЕ(f(x2) < f(x1)) равносильно f(x2) >= f(x1) (5)
с помощью логической функции ЕСЛИ(). Если логическое условие f(x2) >= f(x1), имеет значение ИСТИНА, вывести текст «Неубывающая», иначе «Нет». Провести анализ результатов выполнения условия неубывания на этих интервалах.
|
|
|
3. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение проверив выполнение условие возрастания функции (2) с помощью логической функции ЕСЛИ(). Если логическое условие (2) имеет значение ИСТИНА, вывести текст «Возрастающая», иначе «Нет». Провести анализ результатов выполнения условия возрастания функции на этих интервалах.
Пример 2.1. Исследование функции на возрастание (неубывание) или убывание (невозрастание ) аналитическим способом
Следуя инструкциям Алгоритма 2.1, выполнить следующие действия.
1. Создать электронную таблицу проверки логического условия возрастания функции (1) (рис. 2.1).
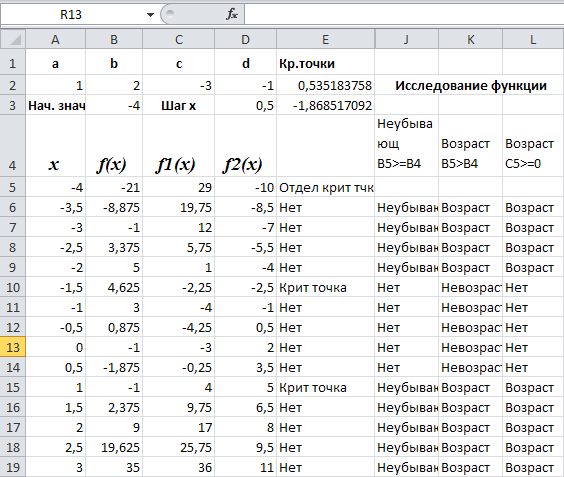
Рис. 2.1. Электронная таблица исследования функции на возрастание и убывание
Выделить диапазон K6:K19, ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия (1) и принятия решения о выполнении условия возрастания функции на интервале [ a,b ], которая имеет вид
=ЕСЛИ(B6>B5; “ Возрастающая ”; “ Невозрастающая ”).
Выполнить копирование формулы в ячейке K6на диапазон (см. рис. 2.1).
Анализ результатов проверки логического условия показывает, что на интервалах [ --4;-2 ] и [ 1;1,5 ] выполняется условие возрастания функции, а на интервале [ -1,5;0,5 ] ‑ условие (1) не выполняется (функция невозрастает).
2. Создать электронную таблицу проверки логического условия возрастания функции (2). Выделить диапазон L6:L19 (см. рис. 2.1), ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении условия возрастания функции (2)на интервале [ a,b ], которая имеет вид
=ЕСЛИ(C6>=0; “Возрастающая”; “Нет”).
Выполнить копирование формулы в ячейке L6 на диапазон (см. рис. 2.1).
Анализ результатов проверки логического условия показывает их идентичность результатам проверки условия (1) (см. п.1).
3. Создать электронную таблицу проверки логического условия неубывания функции (5). Выделить диапазон J6:J19 (см. рис. 2.1), ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении условия неубывания функции (3) на интервале [ a,b ], которая имеет вид
|
|
|
=ЕСЛИ(B6 >=B5; “Неубывающая”; “Нет”).
Выполнить копирование формулы в ячейке J6 на диапазон (см. рис.2.1).
Анализ результатов проверки логического условия (3) показывает, что на интервалах [ --4;-2 ] и [ 1;1,5 ] выполняется условие неубывания функции, а на интервале [ -1,5;0,5 ] ‑ условие не выполняется (функция убывает).
|
|
|


