Исследование функции на экстремум. Поиск максимума и минимума функции

Алгоритм 2.2. Исследование функции на экстремум

Для исследования функции f(x) на интервале [ a,b ] на экстремуманалитическим способом необходимо воспользоваться теоремой математического анализа «Второй достаточный признак существования экстремума функции f(x) на интервале [ a,b ] ».

Теорема 3 «В торой достаточный признак существования экстремума функции f(x) на интервале [ a,b ]». Если производная f1(x) функции f(x) обращается в нуль в точке x₀ или не существует и при переходе через x₀ меняет знак на противоположный, а ее вторая производная f2(x) отлична от нуля, то в точке x₀ функция f(x) достигает экстремума (минимума, если f2(x) >0, и максимума, если f2(x) <0. Предполагается, что f2(x) непрерывна в точке x₀ и ее окрестности. Логическое условие, которое имеет значение ИСТИНА, когда выполняется условие существования экстремума (максимума) функции на интервале [ a,b ], имеет вид (6)

И(f1(a)* f1(b)< 0; f2(b) <0). (6)

Логическое условие, которое имеет значение ИСТИНА, когда выполняется условие существования экстремума (минимума) функции на интервале [ a,b ], имеет вид (6)

И(f1(a)* f1(b)< 0; f2(b) >0). (7)

1. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение условие существования экстремума (максимума) функции на интервале [ a,b ] (6) с помощью логической функции ЕСЛИ(). Если логическое условие (6) имеет значение ИСТИНА, вывести текст «Максимум», иначе «Нет». Провести анализ результатов выполнения существования экстремума (максимума) функции на этих интервалах.

2. Исследовать значения функции f(x) на границах интервалов значений x, заданных таблично, проверив выполнение условие существования экстремума (минимума) функции на интервале [ a,b ] (7) с помощью логической функции ЕСЛИ(). Если логическое условие (7) имеет значение ИСТИНА, вывести текст «Минимум», иначе «Нет». Провести анализ результатов выполнения условия существования экстремума (минимума) функции на интервале [ a,b ] на этих интервалах.

Пример 2.2. Исследование функции на экстремуманалитическим способом. Поиск минимума и максимума функции

Следуя инструкциям Алгоритма 2.2, выполнить следующие действия.

1. Создать электронную таблицу проверки логического условия существования экстремума (максимума) функции (6) (рис.2.2). Выделить диапазон М6:М19, ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении условия существования экстремума (максимума) функции на интервале [ a,b ], которая имеет вид

=ЕСЛИ(И(С6*С5<0; D5<0);“ Максимум ”; “ Нет ”).

Выполнить копирование формулы в ячейке М5 на диапазон (см. рис. 2.2).

Рис. 2.2. Электронная таблица исследования функции на экстремум и точку перегиба

Анализ результатов проверки логического условия показывает, что на интервалах [ -2;-1,5 ] выполняется условие существования экстремума (максимума) функции

f1(-2)=-1; f1(-1,5)=2,25; f1(-2)*f1(-1,5)<0 (производная меняет знак);

f2(-2)=-4< 0; f2(-1,5)=-2,5< 0 (вторая производная величина отрицательная и сохраняет знак на интервале [ -2;-1,5 ]).

Проверка логического условия (6) позволила установить, что максимум функции существует на интервале [ -2;-1,5 ]

f(-2)=5; f(-1,5)=4,625.

Максимум функции принимает значение в диапазоне от 4,625 до 5 (см. рис.2.2). Для определения значения величины максимума функции с заданной точностью eps необходимо вычислить его, подставив значение критической точки -1,8685 в формулу функции. В электронной таблице (рис. 2.2) значение максимума вычисляется по формуле в ячейке М3. Максимум функции равен 5,065. Далее будет рассмотрено уточнение приближенного значения максимума табличным методом, аналогично уточнению приближенных значений критической точки (Алгоритм 2.3, Тема 1) и корня функции Алгоритм 3.1, Тема 1).

На интервале [2,5;3] функция f(x) принимает значения большие 5:

f(2,5)=19,625, f(3)=35.

Но эти значения не могут рассматриваться как максимум функции f(x), т.к. на данном интервале не выполняется условие существования экстремума (максимума) функции:

f1(2,5)=25,75; f1(3)=36; f1(2,5)*f1(3)>0 (производная не меняет знак);

f2(2,5)=9,5> 0; f2(3)=11> 0 (вторая производная величина положительная).

2. Создать электронную таблицу проверки логического условия существования экстремума (минимума) функции (7) (рис. 2.2). Выделить диапазон N6:N19, ввести логическую формулу с функцией ЕСЛИ() для проверки логического условия и принятия решения о выполнении условия существования экстремума (минимума) функции на интервале [ a,b ], которая имеет вид

=ЕСЛИ(И(С6*С5<0; D6>0);“ Минимум ”; “ Нет ”).

Выполнить копирование формулы в ячейке N6на диапазон (см. рис. 2.2).

Анализ результатов проверки логического условия показывает, что на интервале [ 0,5;1,0 ] выполняется условие существования экстремума (минимума) функции

f1(0,5)=-0,25; f1(1,0)=4; f1(0,5)*f1(1,0)<0 (производная меняет знак); f2(0,5)=3,0> 0; f2(1,0)=5>0 (вторая производная величина положительная и сохраняет знак на интервале [ 0,5;1,0 ]).

Минимум функции принимает значение в диапазоне от -1,875 до -1 (см. рис.2.2). Для определения значения величины минимума функции с заданной точностью eps необходимо вычислить его, подставив значение критической точки 0,535 в формулу функции. В электронной таблице (рис. 2.2) значение минимума вычисляется по формуле в ячейке М2. Минимум функции равен -1,879. Далее будет рассмотрено уточнение приближенного значения минимума табличным методом, аналогично уточнению приближенных значений критической точки (Алгоритм 2.3, Тема 1) и корня функции Алгоритм 3.1, Тема 1).

На интервале [-3,5;-4] функция f(x) принимает значения меньшие, чем -1:

f(-3,5)=-8,875, f(-4)=-21.

Но эти значения не могут рассматриваться как минимум функции f(x), т.к. на данном интервале не выполняется условие существования экстремума (минимума) функции:

f1(-3,5)=19,75; f1(-4)=29; f1(-3,5)*f1(-4)>0 (производная не меняет знак);

f2(-3,5)=-8,5> 0; f2(-4)=-10> 0 (вторая производная величина отрицательная).

Пример 2.3. Уточнение приближенного значения максимума (минимума) функции табличным методом

По данным исследования экстремума функции (см. п.1, Пример 2.2) на интервале [ -2;-1,5 ] значений x существует точка максимума функции
[x_макс; f( x_макс ) ]. Следуя инструкциям Алгоритма 2.3 (Тема 1), выполнить следующие действия.

1. Создать электронную таблицу уточнения табличного уточнения точки максимума на интервале [-2;-1,5] (см. рис.2.3). Вычислить ряд значений x на интервале [-2;-1,5]. В ячейках электронной таблицы P24 и P26 нужно ввести начальное значение ряда x=-2 и шаг по x, равный 0,1*(-2;-1,5)=0,05, соответственно (см. рис. 2.3). Выделить ячейку J23 и ввести формулу =P24 для копирования начального значения ряда. Выделить диапазон J24:J29 и ввести формулу =J23+$P$26 в ячейку J24 для вычисления ряда значений x по формуле арифметической прогрессии, которую скопировать на диапазон (<Ctrl+Enter>). Для полученных значений ряда значений x в диапазоне K23:K29 вычислить ряд значений функции f(x), в диапазоне L23:L29 ‑ первой производной f1(x), в диапазоне М23:М29 ‑ второй производной f2(x). (рис. 2.3). Для вычисления f(x), f1(x) и f2(x) нужно выделить соответствующий диапазони ввести формулу или выполнить команды Копировать и Вставить с использованием «Специальная вставка» для вычисления значений f(x), f1(x) и f2(x) из других ячеек электронной таблицы (см. Пример 2.2, Тема 1). Скопировать формулу на диапазон (<Ctrl+Enter>).

Рис. 2.3. Электронная таблица табличного уточнения точки максимума на интервале [-2;-1,5]

2. Исследовать значения первой f1(x) и второй f2(x) производных на границах [-2;-1,5] интервала значений x, заданных таблично, аналитическим методом, проверив выполнение необходимого условия существования экстремума (максимума) (6).Выделить диапазон N24:N29 и в ячейку N24 ввести формулу

=ЕСЛИ(И(L23*L24<0; M24<0); “Максимум”;”Нет”),

которую размножить на диапазон (<Ctrl>+<Enter>). На первой итерации точка максимума отделена на интервале [ -1,9;-1,85 ].

3. Исследовать достижение заданной точности eps оценки точки максимум, на интервалах [ a_i,b_i ], полученных делением интервала [ a,b ] на 10 (см. п.1), проверив логические условия останова процесса уточнения точки максимума

И(½ a_i –b_i ½<eps; ½ f(a_i) –f(b_i) ½<eps; ½ f1(b_i) ½<eps). (8)

Если условия (8) выполняются (погрешность оценки не превышает заданную точность eps), то итерационный процесс уточнения точки максимума функции f(x) на интервале [ a,b ] нужно закончить. За значение точки максимума принимается значение b_i,полученное на последней i- й итерации.

Если условие (8) не выполняется (погрешность оценки превышает заданную точность eps), то итерационный процесс уточнения точки максимума нужно продолжить, повторив пп.1-3 для интервала [ a_i,b_i ]. По данным интервала [ a_i,b_i ], на котором существует точка максимума (см. п.2), вычислить ряд значений x для интервала [ a_i,b_i ]. Для этого в ячейках электронной таблицы, в которых на первой итерации были заданы начальное значение и шаг, нужно заменить начальное значение ряда x=a_i и шаг по x, равный 0,1*(b_i-a_i). В результате замены будет выполнен автоматически пересчет рядов значений x, функции, первой и второй производных.

4. Выделить диапазон O24:O29 и в ячейку O24 ввести формулу

=ЕСЛИ(И(ABS(J23-J24)<P28; ABS(K23-K24)<P28; ABS(M24)<P28)); “Точность достигнута”;”Нет”),
которую размножить на диапазон (<Ctrl>+<Enter>) (см. рис. 2.3). Точка максимума, которая отделена на интервале [ -1,9,-1,85 ], не удовлетворяет требованиям заданной точности.

½ f(-1,9)-f(-1,85) ½ = ½ 5,061-5,063 ½>eps=0,001

Условие (8) не выполняется (погрешность оценки превышает заданную точность eps) и итерационный процесс уточнения критической точки нужно продолжить, повторив пп.1-3 для интервала [ -1,9;-1,85 ]. Для этого в ячейках электронной таблицы P24 и P26 нужно ввести новое начальное значение интервала (-1,9) и шага по x, равного 0,005, соответственно. В результате замены будет выполнен автоматически пересчет рядов значений x и производной f1(x).

Условие (8) выполняется (погрешность оценки не превышает заданную точность eps) на интервале [ -1,869;-1,865 ]: (см. рис. 2.4)

½- 1,869;-1,8685 ½<eps=0,001;

½ f(-1,869)-f(-1,8685) ½ = ½ 5,064604-5,064605 ½<eps=0,001;

½ f1(-1,8685) ½ = ½ -0,00012 ½<eps=0,001/

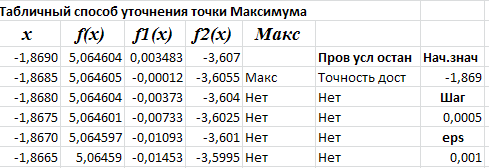
Рис. 2.4. Электронная таблица уточнения координат точки максимума функции на интервале [-2;-1,5] табличным методом

Итерационный процесс уточнения точки максимума функции f(x) на интервале [ -1,869;-1,865 ] нужно закончить. За значение координат точки максимума [x_макс; f( x_макс ) ] принимается значения [- 1,865;5,0646 ], наодной изграниц интервала на последней итерации.

5. Уточнить координаты точки минимума функции [x_мин; f( x_мин ) ]на интервале [0,5;1,0] табличным методом, повторив пп. 1-6.

Исследовать достижение заданной точности eps оценки точки максимум, на интервалах [ a_i,b_i ], полученных делением интервала [ a,b ] на 10 (см. п.1), проверив логические условия останова процесса уточнения точки минимума

И(½ a_i –b_i ½<eps; ½ f(a_i) –f(b_i) ½<eps; ½ f1(b_i) ½>eps). (9)

Если условия (9) выполняются (погрешность оценки не превышает заданную точность eps), то итерационный процесс уточнения координат точки маинимума функции f(x) на интервале [ a,b ] нужно закончить. За значение точки минимума принимается значение b_i,полученное на последней i- й итерации (рис. 2.5).

Условие (9) выполняется (погрешность оценки не превышает заданную точность eps) на интервале [ 0,535;0,5352 ]: (см. рис. 2.5)

½ 0,535-0,5352 ½<eps=0,001;

½ f(0,535)-f(0,5352) ½ = ½ -1,87942;-1,87942 ½<eps=0,001;

½ f1(0,5352) ½ = ½ 0.00017 ½<eps=0,001/

Рис. 2.5. Электронная таблица уточнения координат точки минимума функции на интервале [0,5;1,0] табличным методом

За значение координат точки минимума [x_мин; f( x_мин ) ] принимается значения [0,5352;-1,87942], награнице интервала на последней итерации.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: