 |
Отложение характерных точек на графике функции
|
|
|
|
Алгоритм 3.1. Отложение характерных точек на графике функции
Характерные точки функции:
· Точки максимума функции с координатами [xмакс;f(xмакс)] (см. Пример 2.3).
· Точки минимума функции с координатами [xмин;f(xмин)] (см. Пример 2.3).
· Точки перегиба функции [xтп;f(xтп)] (см. Пример 2.5).
1. Отобразить ряды значений «Ряд Х», «Ряд f(x)», «Ряд f1(x)» и «Ряд f2(x)» на точечной диаграмме (см. рис. 2.7). Выбрать на Ленте вкладку Вставить, далее в разделе Диаграммы выбрать тип диаграммы ‑ щелкнуть кнопку Точечная. В открывшемся меню выбрать подтип Точечной диаграммы – Точечна я с гладкими краями.
2. Выполнить форматирование оси Ох и оси Оy на диаграмме на вкладке Параметры оси диалоговое окно Формат оси с учетом требований по точности отображения значений координат характерных точек.
3. На графике функции f(x) и ее первой производной f1(x) отложить координаты точек максимума функции f(x) [xмакс;f(xмакс)] и минимума функции f(x) [xтп;f(xтп)].
4. На графике функции f(x) и ее второй производной f2(x) отложить координаты точки перегиба функции f(x) [xтп;f(xтп)].
Пример 3.1. Отображениехарактерных точек на графике функции
Следуя инструкциям Алгоритма 3.1
Пример 3.1.
1. Отобразить ряды значений x, f(x) и f1(x) на точечной диаграмме (см. рис. 2.2). Выделить диапазон А5:С19, содержащий значения базовых рядов «Ряд Х», «Ряд f(x)» и «Ряд f1(x)» для отображения на диаграмме. Выбрать на Ленте вкладку Вставить, далее в разделе Диаграммы выбрать тип диаграммы ‑ щелкнуть кнопку Точечная. В открывшемся меню выбрать подтип Точечной диаграммы – Точечна я с гладкими краями (рис.2.4).
7. Выполнить форматирование оси Х на диаграмме. Вызвать диалоговое окно Формат оси, выделив ось Х на диаграмме, установив указатель мыши на оси и щелкнув правой кнопкой (рис. 2.5). В контекстном меню выбрать команду Формат оси. В диалоговом окне Формат оси на вкладке Параметры оси, которая открывается по умолчанию (рис. 2.6),установить значения в окнах: минимальное значение (по оси ОХ) фиксированное - -2,0; максимальное значение (по оси ОХ) фиксированное - -1,75; цена основных делений и цена промежуточных делений – фиксированные 0,05 и 0,01, соответственно.
|
|
|
8. На графике первой производной функции f1(x) найти координаты критических точек функции f(x) и исследовать график функции f(x) в окрестности критических точек. Функция f(x) принимает экстремальные значения при значениях x=-1,8 и x=0,5, соответствующих нулям первой производной функции f1(x)=0 (значения определены по диаграмме приближенно).
9. Вызвать, выделив ось Х на диаграмме, установив указатель мыши на оси и щелкнув правой кнопкой (рис. 2.5). В контекстном меню выбрать команду Формат оси. В диалоговом окне Формат оси, которая открывается по умолчанию (рис. 2.6),установить значения в окнах: минимальное значение (по оси ОХ) фиксированное - -2,0; максимальное значение (по оси ОХ) фиксированное - -1,75; цена основных делений и цена промежуточных делений – фиксированные 0,05 и 0,01, соответственно.
1. Форматирование элементов диаграммы
Приложение 1
Задания по темам 1 и 2.
| № вар | Задание | a | b | c |
| 1. | Найти наименьший положительный корень уравнения f(x)=0, где f(x)=tg ax ‑ bx | 0,6319 | 0,9217 | |
| 9,4637 | 13,8249 | |||
| 0,9464 | 1,3825 | |||
| 8,5174 | 12,4424 | |||
| 1,8927 | 2,765 | |||
| 4,4164 | 6,4516 | |||
| Найти больший корень уравнения f(x)=0, где f(x)=ln(ax) – bx +c | 0,3049 | 0,3436 | 1,5 | |
| 9,1464 | 10,3081 | 1,5 | ||
| 0,6098 | 0,6872 | 1,5 | ||
| 8,5366 | 9,6209 | 2,0 | ||
| 0,9146 | 1,0308 | 2,5 | ||
| 7,9268 | 8,9337 | 3,0 | ||
| Найти наименьший положительный корень уравнения f(x)=0, где f(x)=asin bx ‑ cx | 0,33 | 2,3 | 0,5 | |
| 7,375 | 7,75 | |||
| 2,2 | ||||
| 6,3 | 5,189 | |||
| 1,67 | 2,5 | 1,5 | ||
| 6,18 | 6,25 | |||
| Найти второй положительный корень уравнения f(x)=0, где f(x)= cos ax ‑ bx | 0,33 | 2,3 | ||
| 7,375 | ||||
| 2,2 | ||||
| 6,3 | 5,189 | |||
| 1,67 | 2,5 | |||
| 6,18 |
|
|
|
Приложение 2.
Исследование области существования и определения функции y=f(x)
(см. Приложение 1)
1. Дана f(x)=tg ax-bx.
Каждому действительному числу a (как радианной мере угла), такому, что a¹(p/2+ kp)/a, где k – любое целое число, можно поставить в соответствие одно действительное число y= tg a a -b a. То есть область существования функции y= tg ax-bx – множество всех действительных чисел [-¥,+¥], кроме чисел x=( p/2+ kp)/a, где k – любое целое число. Если по условию задачи, нужно найти наименьший положительный корень уравнения f(x)=0, то область определения функции y=f(x), есть интервал между первой критической точкой функции Xкр1=acos(c/(ab))/b и точкой разрыва [ Xкр1, Xтр2 ] (см. Приложение 3).
2. Дана f(x)=loga x
Пусть a – некоторое фиксированное положительное, не равное единице число, тогда каждому положительному числу b можно поставить в соответствие одно число y= loga b, т.е. области существования функции y=loga x – множество всех положительных чисел. Если по условию задачи, нужно найти наибольший положительный корень уравнения f(x)=0, то область определения функции y=f(x), есть множество положительных чисел, больших значения критической точки функции [ Xкр ], (см. Приложение 3).
3. Дана f(x)=asin bx-cx
Каждому действительному числу a (как радианной мере угла) можно поставить в соответствие одно действительное число y= asinb a -c a. То есть область существования функции y=asin bx - cx – это множество всех действительных чисел [-¥,+¥]. Если по условию задачи, нужно найти наименьший положительный корень уравнения f(x)=0, то область определения функции y=f(x), есть интервал между первой и второй критическими точками функции [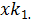 
, 
] (см. Приложение 3).
4. Дана f(x)=cos ax‑bx.
Область существования функции y= cos ax‑bx – множество всех действительных чисел [-¥,+¥] (аналогична функции f(x)=sin x, см. п.2 ). Если по условию задачи, нужно найти второй положительный корень уравнения f(x)=0, то область определения функции y=f(x), есть интервал между второй и третьей критическими точками функции [ , 
] (см. Приложение 3).
Приложение 3.
Определение формул для вычисления критических точек функций
(см. Приложения 2)
|
|
|
1. Дана f(x)=tg ax-bx.
Область существования функции y= tg ax-bx – множество всех действительных чисел [-¥,+¥], кроме чисел xТР=( p/2+ kp)/a (точки разрыва), где k – любое целое число.
Формула для первой производной f1(x)=a/cos2 ax ‑ b
Формула для первой критической точки функции xk1, =acos(c/(ab))/b;
Формула для первой точки разрыва xТР1= p/(2 a).
Формула для второй производной f2(x)=2a2sin ax/cos3ax
2. Дана f(x)=loga x
Формула для первой производной f1(x)=1/x‑b
Формула для критической точки функции xk1=1/b.
Формула для второй производной f2(x)=‑1/x2.
3. Дана f(x)=asin bx-cx.
Формула для первой производной f1(x)=abcos bx-c
Формула для критической точки 
=2kp/b 
, k =0,1,2…
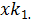=arccos(c/(ab))/b; =2p/b‑ 
Формула для второй производной f2(x)=‑ ab2 sin bx
4. Дана f(x)=cos ax‑bx.
Формула для первой производной f1(x)=‑asin ax‑b.
Формула для критической точки = 
, где q =0,1,2…
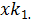= ‑arcsin(‑a/b)/b; = ‑arcsin(‑a/b)/b+p/b; =arcsin(‑a/b)/b+2p/b.
Формула для второй производной f2(x)=‑a2 cos ax
|
|
|
