 |
Числовые характеристики случайных величин
|
|
|
|
Выше мы познакомились с исчерпывающими характеристиками случайных величин.
Для дискретной случайной величины это:
1) функция распределения;
2) ряд распределения (графически – многоугольник распределения).
Для непрерывной случайной величины это:
1) функция распределения;
2) плотность распределения (графически - кривая распределения).
На практике зачастую нет возможности или необходимости характеризовать случайную величину полностью. Достаточно указать только отдельные числовые параметры, характеризующие основные черты распределения случайных величин: например, какое-то среднее значение, около которого группируются возможные значения случайной величины; какое-либо число, характеризующее степень разбросанности этих значений относительно среднего. Такие характеристики называются числовыми характеристиками случайной величины. Важнейшими числовыми характеристиками являются математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины
Математическим ожиданием дискретной случайной величины называется сумма произведений всех её возможных значений на их вероятности.
Пусть случайная величина X принимает n возможных значений. Тогда её математическое ожидание M(X) равно
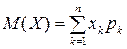(9)
Если дискретная случайная величина X принимает счетное множество значений, то
, (10)
причем математическое ожидание существует, если ряд в правой части равенства (10) сходится абсолютно.
Можно показать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Для непрерывной случайной величины с плотностью f(x) математическое ожидание выражается уже не суммой, а интегралом.
|
|
|
Математическим ожиданием непрерывной случайной величины называется интеграл
, (11)
где f(x)- плотность распределения величины Х.
Отклонением случайной величины X называется разность между случайной величиной и её математическим ожиданием: Х - М (Х).
Дисперсия случайной величины – это характеристика рассеивания значений случайной величины около её математического ожидания, определяемая по формуле
, (12)
то есть дисперсия равна математическому ожиданию квадрата отклонения случайной величины от её математического ожидания.
Для непрерывной случайной величины имеем:
. (13)
Дисперсию часто вычисляют по формуле
(14)
- дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом её математического ожидания.
Дисперсия случайной величины имеет размерность квадрата случайной величины, в то время как математическое ожидание имеет размерность самой случайной величины. Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученную величину называют среднеквадратическим отклонением случайной величины:
(15)
Основные распределения дискретных случайных величин
Распределение Бернулли
Производится один опыт (или наблюдение), в котором может произойти или не произойти событие А. Вероятность того, что событие А произойдет, равна числу p. Один такой опыт, в котором возможны лишь два исхода («успех» и «неудача»), называют испытанием Бернулли.
Пусть случайная величина X характеризует появление события А в данном опыте, то есть
Тогда p{X = 1} = p(A) = p; p{X = 0} = p(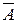
) = 1 – p = q. Говорят, что случайная величина X распределена по Бернулли. Функция распределения такой величины имеет вид
(16)
Такая величина может возникнуть, например, при бросании монеты (событие А – выпадение орла, р(А) = 0,5, р(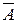) = 0,5), при бросании игральной кости (событие А - выпадение пяти очков, р(А) = 1/6, р(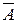) = 5/6).
|
|
|
Запишем ряд распределения и найдём числовые характеристики распределения Бернулли:
| X | ||
| p | p | 1-p |
| X 2 | 12 | 02 |
| p | p | 1-p |
.
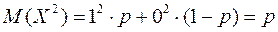Тогда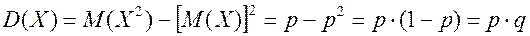 
.
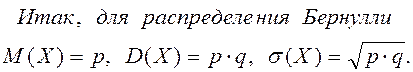
| (17) |
|
|
|
