 |
Гипергеометрическое распределение
|
|
|
|
Многие задачи комбинаторики могут быть сведены к следующей модели. Пусть имеется N элементов, среди которых M элементов красного цвета и N-M элементов черного цвета. Случайным образом выбирается группа из n элементов.
Случайная величина Х – число элементов красного цвета среди отобранных n элементов. Ясно, что Х может принимать любые целые значения от 0 до наименьшего из чисел {n,M}.
Найдем вероятность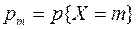 
- вероятность того, что случайная величина Х примет значение, равное m, или, другими словами, что среди отобранных n элементов окажется ровно m красных.
Заметим, что выбранная группа состоит из m красных и n-m черных элементов. Красные элементы могут быть выбраны 
различными способами, а черные - 
способами. Так как любой выбор красных элементов может комбинироваться с любым выбором черных, имеем:
. (25)
Определённый таким образом набор вероятностей называется гипергеометрическим распределением.
Итак, случайная величина Х имеет гипергеометрическое распределение, если она принимает целые значения m = 0, 1, 2, …, min{n,M} с вероятностями
. (26)
Пример 2.5.1. В комитете каждый из 50 американских штатов представлен двумя сенаторами. Найти вероятность того, в комиссии из 50 случайно выбранных сенаторов представлен конкретный штат.
Решение. Обозначим Х = число сенаторов, представляющих данный штат. Из условия задачи следует, что N = 100 (всего сенаторов), M = 2(число сенаторов, представляющих данный штат), n = 50 (число сенаторов в комиссии).
Данный штат будет представлен в комиссии, если Х = 1 или Х = 2, то есть искомая вероятность равна
Ответ: 0,72525.
Математическое ожидание дискретной случайной величины, имеющей гипергеометрическое распределение, есть
|
|
|
, (27)
а её дисперсия
. (28)
Гипергеометрическое распределение определяется тремя параметрами: N, M, n. Если n мало по сравнению с N (практически при 
), он приближается к биномиальному распределению с параметрами n и 
, то есть
. (29)
Гипергеометрическое распределение часто используется при решении задач, связанных с контролем качества продукции.
Пример 2.5.2. В группе из 21 деталей пять отличного качества. Из этой группы наудачу отбираются три детали. Составить закон распределения случайной величины Х – числа деталей отличного качества среди отобранных. Найти M(X).
Решение. Случайная величина Х принимает значения 0, 1, 2, 3. Вероятности этих значений находим по формуле (26) при M = 5, N = 21:
Ряд распределения имеет вид:
| Х | ||||
| р | 0,4211 | 0,4511 | 0,1203 | 0,0075 |
Значение M(X) найдём двумя способами: а) по ряду распределения: M(X) = 
б) по формуле (27) M(X) = 
Основные распределения непрерывных случайных величин
Равномерное распределение
Понятие равномерного распределения соответствует представлению о выборе точки из определенного отрезка наудачу.
Случайная величина X распределена равномерно на отрезке [a,b], если ее плотность постоянна и равна
 
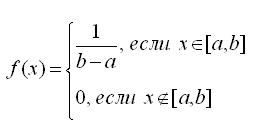
| (30) |
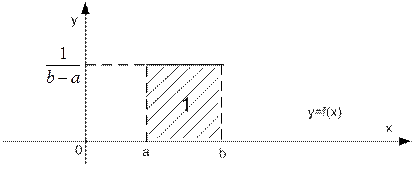
Рис. 3. График плотности вероятности равномерного распределения
Из-за внешнего вида графиков плотности равномерные распределения называют «прямоугольными».
Убедимся, что интеграл от минус бесконечности до плюс бесконечности от плотности вероятности равномерного распределения равен 1:
Найдём функцию распределения вероятностей:
| (31) |
Рис. 4. График функции распределения вероятностей
для равномерного распределения
Пример 3.1.1. Пусть производятся измерения по некоторой шкале
Здесь - расстояние между делением и истинным значением – это случайная величина, равномерно распределенная на отрезке, длина которого равна расстоянию между делениями.
|
|
|
Пример 3.1.2. Время ожидания пассажира, прибывшего на автобусную остановку без учета расписания, можно рассматривать как случайную величину, равномерно распределенную в интервале между последовательными отъездами автобусов.
Пример 3.1.3. Интервал времени между отправлениями поездов метрополитена равен 3 мин. Найти вероятность того, что человек, пришедший на станцию метро в случайный момент времени, будет ждать не более одной минуты.
Решение. Время ожидания поезда можно считать случайной величиной, имеющей равномерное распределение на отрезке [0;3]. Вероятность того, что человек будет ждать не более одной минуты, равна значению функции распределения в точке х = 1, то есть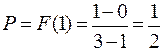 
. Ответ: 0,5.
Найдём числовые характеристики равномерного распределения:
.
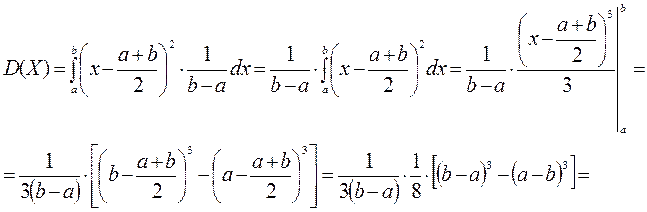
Итак, если непрерывная случайная величина имеет равномерное распределение, то её числовые характеристики определяются следующими формулами:
| (32) |
|
|
|
