 |
Биномиальное распределение
|
|
|
|
Пусть производится n независимых опытов, в каждом из которых может произойти (с вероятностью р) или не произойти (с вероятностью 1- р = q) некоторое событие А, то есть производится n независимых испытаний Бернулли. Повторные независимые испытания Бернулли называют схемой Бернулли.
Рассмотрим случайную величину Х, равную числу «успехов» в схеме Бернулли. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться один раз, либо два раза, …, либо n раз. Таким образом, возможные значения Х таковы: 
Вероятности этих возможных значений определяются формулой Бернулли:
, (18)
где k = 0, 1, 2, …, n.
Формула (18) и является аналитическим выражением биномиального распределения. Другими словами, биномиальным называют распределение вероятностей, определяемое формулой Бернулли (18). Закон назван «биномиальным» потому, что правую часть равенства (18) можно рассматривать как общий член разложения бинома Ньютона:
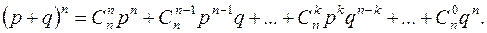(19)
Запишем биномиальный закон в виде таблицы:
| Х | … | k | … | n - 1 | n | |||
| Р | 
| 
| 
| … |  
| … | 
| 
|
Контроль: 
Функция распределения случайной величины Х, подчиняющейся биномиальному закону, имеет вид:
(20)
Найдем числовые характеристики биномиального распределения. Обозначим через 
- число появлений события А в первом испытании, 
- число появлений события А во втором испытании, …, 
число появлений события А в n-ном испытании. Тогда Х – число появлений события А во всех n испытаниях - равно сумме 
, а математическое ожидание Х в силу независимости случайных величин , , …, равно сумме их математических ожиданий:
n
Аналогичным образом получаем формулу для дисперсии биномиального распределения:
.
| (21) |
Пример 2.2.1. Длительной проверкой качества деталей установлено, что 75% деталей не имеют дефектов. Составить закон распределения случайной величины Х – числа пригодных деталей среди наудачу взятых шести деталей - и найти числовые характеристики этой случайной величины.
|
|
|
Решение. Случайная величина Х распределена по биномиальному закону, при этом n = 6, p = 0,75, q = 0,25. По формуле (18) находим:
Закон распределения случайной величины Х в виде таблицы имеет вид:
| Х | |||||||
| р | 0,0002 | 0,0044 | 0,0330 | 0,1318 | 0,2966 | 0,3560 | 0,1780 |
Контроль: 
0,0002+0,0044+0,0330+0,1318+0,2966+0,3560+0,1780=1.
Распределение Пуассона
Дискретная случайная величина Х имеет распределение Пуассона, если её возможные значения равны 0, 1, 2, …, k, …, а соответствующие вероятности выражаются формулой Пуассона
. (22)
Распределение Пуассона является предельным для биномиального распределения, когда 
и 
так, что 
- постоянно.
Распределение Пуассона иногда называют законом редких событий, так как вероятности (22) дают приближенное распределение числа наступлений некоторого маловероятного (редкого) события при большом числе независимых испытаний. Примерами случайных величин, имеющих распределение Пуассона, являются: число вызовов на телефонной станции за некоторое время, число опечаток в большом тексте, число бракованных деталей в большой партии и так далее.
Правомерность использования закона Пуассона вместо биномиального распределения при большом числе испытаний даёт следующая теорема:
Теорема Пуассона. Если в схеме Бернулли ; так, что , то 
при любых k, k = 0, 1, 2, …
Доказательство. Представим биномиальную вероятность в виде
При имеем
Отсюда получаем: при , что и требовалось доказать.
Пример 2.3.1. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут ровно три негодных изделия.
|
|
|
Решение. По условию n = 5000; p = 0,0002, k = 3. Найдём 
:
= np = 
По формуле Пуассона искомая вероятность приближенно равна
Ответ: 0,06.
Случайная величина Х, распределённая по закону Пуассона, имеет следующий ряд распределения:
| Х | … | k | … | |||
| р | 
| 
| 
| … | 
| … |
Контроль: 
Найдем числовые характеристики случайной величины Х, распределённой по закону Пуассона.
;
| … | 
| … | ||||
| P |
|
|
| 
| … |
| … |
Для того, чтобы найти сумму полученного ряда, рассмотрим ряд Тейлора для функции :
.
Умножим обе его части на 
: 
и полученный ряд продифференцируем:
Полученный ряд ещё раз умножаем на
Следовательно, 
.
Тогда 
| (23) |
Параметр пуассоновского распределения равен одновременно математическому ожиданию и дисперсии случайной величины Х, имеющей это распределение. В этом состоит отличительная особенность данного распределения, которая используется на практике: на основании опытных данных находят оценки для математического ожидания и дисперсии; если они близки между собой, то есть основание считать, что случайная величина распределена по закону Пуассона.
|
|
|
