 |
Показательное (экспоненциальное) распределение
|
|
|
|
Экспоненциально распределенной называется такая случайная величина, для которой плотность вероятности имеет вид
| (33) |
Здесь 
- параметр распределения.
Проверим, что это плотность распределения:
, что и требовалось доказать.
Функция распределения вероятностей показательного распределения имеет вид
| (34) |
Графики f(x) и F(x) представлены на рис. 5.
Рис. 5. Графики плотности вероятности и функции вероятности для
показательного (экспоненциального) распределения
Найдём числовые характеристики показательного распределения:
*) Интегрируем по частям:
Итак, если непрерывная случайная величина имеет показательное распределение, то её числовые характеристики определяются по формулам:
| (35) |
Найдём вероятность попадания случайной величины Х, распределённой по показательному закону, в интервал (a,b). Используя формулы (3) и (34), получаем
(36)
Пример 3.2.1. Случайная величина Т – время работы радиолампы имеет показательный закон распределения. Найти вероятность того, что лампа проработает не менее 800 часов, если среднее время работы радиолампы 400 часов.
Решение. Имеем: M(T) = 400, значит, (см. формулы (35)) 
. Искомая вероятность 
Ответ: 0,135.
Показательный закон распределения – единственный из законов распределения, который обладает свойством «отсутствия последействия» (то есть если промежуток времени Т уже длился некоторое время 
, то показательный закон распределения остаётся таким же и для оставшейся части Т - промежутка). Считают, что время жизни атома имеет показательное распределение Свойство отсутствия последействия имеет следующий смысл: каков бы ни был настоящий возраст, оставшееся время жизни не зависит от прошлого и имеет то же самое распределении, что и само время жизни.
|
|
|
Использование показательного распределения в математических моделях реальных явлений обычно связано именно с этим характерным свойством.
Показательное распределение используется в приложениях теории вероятностей, особенно в теории массового обслуживания (ТМО), в физике, в теории надежности. Оно используется для описания распределения случайной величины вида: длительность работы прибора до первого отказа, длительность времени обслуживания в системе массового обслуживания и так далее.
Рассмотрим, например, непрерывную случайную величину Т - длительность безотказной работы прибора. Функция распределения случайной величины Т, то есть F(t) = P{T < t}, определяет вероятность отказа за время длительностью t. Значит, вероятность безотказной работы за время t равна R(t) = P{T > t} =1 – F(t). Функция R(t) называется функцией надёжности.
Случайная величина Т часто имеет показательное распределение. В этом случае функция надёжности имеет вид R(t) = 1- F(t) = 1 – (1 - 
, то есть 
интенсивность отказов, то есть среднее число отказов в единицу времени.
Пример 3.2.2. Время обслуживания клиента на станции техническогообслуживания имеет показательное распределение, причём чем дольше обслуживают в среднем каждого клиента, тем меньше значение параметра 
.
Нормальное распределение
Непрерывная случайная величина Х имеет нормальное распределение с параметрами а и 
, если её плотность распределения имеет вид:
(37)
Нормальный закон распределения (также называемый законом Гаусса) играет исключительную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это наиболее часто встречающийся на практике закон распределения. Его главная особенность – то, что он является предельным законом, к которому приближаются другие законы распределения при часто встречающихся типичных условиях. Нормальный закон может проявляться как точное решение некоторых задач (в рамках принятой математической модели исследуемого явления). Классические примеры возникновения нормального распределения как точного принадлежат К. Гауссу (закон распределения ошибок наблюдения) и Дж. Максвеллу (закон распределения скорости молекул).
|
|
|
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Исследуем функцию 
. (38)
1) Функция определена на всей оси Ох; D(y) = R.
2) Для всех x 
значение y > 0, то есть график функции (38) (нормальная кривая) расположен над осью абсцисс.
3) 
, то есть ось Ох служит асимптотой графика функции.
4) Исследуем функцию на экстремум:
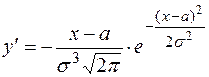; (39)
при x - a = 0, т.е. при х = а; 
при x < a, 
при x > a.
Следовательно, функция имеет максимум при х = а, 
.
5) Разность x - a содержится в аналитическом выражении функции в квадрате, значит, график функции симметричен относительно прямой x = a.
6) Исследуем функцию на точки перегиба:
; (40)
при 
, то есть при 
и 
. При переходе через эти точки 
меняет знак, следовательно, они являются точками перегиба.
График функции (38) приведён на рис. 6.
Рис. 6. Общий вид нормальной кривой
|
|
|
