Парадоксы голосования и причины их возникновения.

 

Анализ рассмотренных примеров уже показал, что абсолютно демократическим способом можно выбрать такого победителя, который по мнению абсолютного большинства избирателей является наихудшим.

Почему возникает такой парадокс? Ведь никаких нарушений демократичных процедур голосования не было, решение принималось исключительно на основе мнения избирателей!

Оказывается, процедуры голосования обладают или не обладают теми или иными свойствами. Рассмотрим некоторые из этих свойств.

Монотонность. Предположим, что кандидат выбирается (среди победителей) при данном профиле голосования и профиль изменится только так, что положение кандидата улучшается, а относительное сравнение пары любых других кандидатов для избирателя остается неизменным. Тогда кандидат для нового профиля по-прежнему должен быть выбран (вновь среди победителей).

Требованию монотонности не удовлетворяет, например, правило относительного большинства с выбыванием, которое широко используется при выборах в Украине.

 

Пример 4. В четырех избирательных группах, с количеством избирателей соответственно 6, 5, 4 и 2 определяется победитель из трех кандидатов: . Мнения избирателей представлены в профиле А:

Профиль А:

I	II	III	IV
a	c	b	b
b	a	c	a
c	b	a	c

По правилу относительного большинства во второй тур проходят и и побеждает (11 голосов против 6).

Предположим, что профиль А – это данные социологического опроса. И было решено провести активную агитацию в наименьшей из избирательных групп. Получилин овый профіль голосования:

Профиль Б:

I	II	III	IV
a	c	b	a
b	a	c	b
c	b	a	c

В этом профиле кандидат улучшил свои позиции в четвертой избирательной группе – вышел на первое место.

Определим победителя по профилю Б.

Кандидат теперь уверенно выигрывает в 1-ом туре и … проигрывает во 2-ом туре кандидату , т.е. улучшение позиции кандидата привело к его поражению.

Как же так? В профиле Б произошло только улучшение положения кандидата ! Вопрос: на чьи деньги проводили агитацию в четвертой избирательной группе?

Таким образом, по правилу относительного большинства с выбыванием может быть выгодно специально проиграть выборы на некотором участке, чтобы вывести во второй тур соперника, у которого можно выиграть заключительный тур выборов. В истории известны такие случаи.

Анонимность. Имена избирателей не имеют значения: если два избирателя поменяются голосами, то результаты выборов не изменятся.

Это условие требует, чтобы мнения всех избирателей были равноценными для процедуры голосования. Такое требование реализуется принципом равноправия избирателей.

Однако, существуют процедуры голосования сознательно придающие мнению одного или части избирателей больший вес (например, председатель правления или члены правления имеют два голоса). Или, например, упорядочение судейских голосов, которое активно используется спортивными отделами газет для определения мест, занятых спортивными командами и передачи информации комментаторами по телефону. Примером такой процедуры является также право вето, которым обладают постоянные члены Совета Безопасности ООН.

Может оказаться, что внешне равноправная процедура на самом деле такой не является. ("На совете мнения разделились. Хотя обе стороны упорно стояли на своём, но победило мнение царей." Геродот, "История")

 

Нейтральность. Имена кандидатов не имеют значения. Если мы поменяем местами кандидатов и в предпочтении каждого избирателя, то исход голосования изменится соответственно (если раньше выбирался , то теперь будет выбираться и наоборот; если выбирался некоторый кандидат 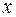, отличный от и , то он же и будет избран.

Это свойство также реализуется принципом равноправия кандидатов.

Но существуют процедуры сознательно нарушающие это требование. Например, на голосование ставится поправка к некоторому существующему положению (законопроекту, Конституции). При этом часто требуется для внесения поправки получить больше, например, 2/3 голосов избирателей, т.е. поправка и существующее положение находятся в неравноправном положении.

Иногда неравноправие возникает неявно.

Правило Копленда и Симпсона анонимны и нейтральны, если мы рассматриваем их как отображения, ставящие в соответствие каждому профилю предпочтений подмножество победителей.

Правило Борда также анонимно и нейтрально. Это же справедливо для для правила голосования с подсчетом очков, если очки разные: .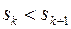

Если ввести некоторое правило при равенстве очков, выделяющее единственного победитля, то либо анонимность, либо нейтральность нарушатся. Это очевидно следует из рассмотрения примера 0:

Виктор	Юлия	Александр
a	b	c
b	c	a
c	a	b

 

Пример 5. Предположим, что на некотором заседании по правилу голосования с последовательным исключением производится отбор альтернативного законопроекта (технического проекта, нового образца для производства и т.п.). Мнения участников заседания приведены в следующей таблице

I	II	III	IV
d	a	d	b
b	b	c	c
a	c	a	d
c	d	b	a

Председатель заседания ставит на голосование проекты в последовательности 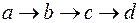. Так как, то при первом голосовании во второй тур выходит , при втором голосовании и на третий тур выходит опять . На заключительном туре 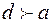и, следовательно, побеждает .

Легко проверить, что при последовательном сравнении побеждает , при побеждает и при побеждает .

Таким образом, используя то, что голосование с последовательным исключением не является нейтральным, председатель заседания может в рассматриваемом случае за счет выбора соответствующей последовательности рассмотрения добиться любого результата голосования.

 

Оптимальность по Парето. Если кандидат для всех лучше кандидата , то кандидат не может быть победителем.

Пример 6. Рассмотритм следующую таблицу:

I	II	III
b	a	c
a	d	b
d	c	a
c	b	d

По правилу голосования с последовательным исключением при использовании последовательности 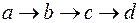имеем , далее второй тур ‑ , в третьем туре , следовательно, побеждает . В то же время кандидат для всех избирателей лучше кандидата .

Из примера 6 видно, что правило голосования с последовательным выбыванием (олимпийская система) не является оптимальным по Парето.

Правило Копленда и Симпсона оптимальны по Парето, Правило Борда также оптимально по Парето. Это же справедливо для правила голосования с подсчетом очков, если очки разные: .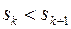

 

Пример 7. Четыре кандидата борятся за звание победителя. Избиратели сгруппированы в 4 группы и имеют следующие предпочтения:

I	II	III	IV
a	a	d	b
d	d	b	c
c	b	c	a
b	c	a	d

По предварительным данным, победитель по Симпсону – . Победителя по Кондорсе нет.

Четыре студента, обсуждая избирательную кампанию в пивбаре, пришли к общему мнению по поводу кандидатов: и решили принять участие в выборах. С их приходом профиль голосования меняется:

I	II	III	IV	V
a	a	d	b	c
d	d	b	c	a
c	b	c	a	b
b	c	a	d	d

Теперь победитель по Симпсону –. Пришедшие избиратели считали, что , то есть они поддержали кандидата , но в результате такой поддержки кандидат проиграл выборы. («парадокс неучастия» - лучше бы эти студенты остались допивать пиво и не участвовали в выборах).

 

Таким образом, можно сформулировать еще одно требование к процедурам голосования в виде аксиомы:

Аксиома участия. Пусть кандидат является победителем для избирателей из множества . Рассмотрим некоторого избирателя и определим победителя при объединенном множестве избирателей . Тогда должен быть избран либо кандидата , либо кандидат, который для избирателя строго лучше, чем .

 

К сожалению нельзя указать лучшую для всех случаев процедуру голосования. Из приведенных примеров видно, что прежде, чем какое-то из правил голосования принимать как процедуру, объединяющую мнения отдельных избирателей в коллективное мнение, нужно глубоко проанализировать эту процедуру, оценить все «за» и «против», и только потом законодательно утверждать такой выбор. Выбор процедуры голосования для каждой конкретной ситуации носит принципиальный характер.

 

А теперь одна история из жизни известнейшего математика австралийского происхождения, который только в 20 лет начал серьезно изучать математику под влиянием книги Бертрана Рассела «Введение в философию математики» и уже в 24 года получил докторскую степень за теорему о полноте предикативной логики (которая сейчас входит в любой курс логики), а в 25 лет доказал теорему о неполноте, которая навсегда прославила его имя.

 

 

Это
Курт Гедель.

 

 

В 1940 году он, спасаясь от нацистов, перебрался в США и работал в университете в Принстоне. В 1948 году ему нужно было пройти собеседование для получения американского гражданства. Это что-то вроде устного экзамена на знание конституции США. Как известно, ее признают величайшим творением политической мысли.

Досконально изучив конституцию США, Гедель незамедлительно пришел к выводу, что в этой стране законным путем может быть установлена диктатура.

Одним из двух поручителей Геделя был Альберт Энштейн.

Гедель поделился с ним своим выводом. В ответ Энштейн настоятельно рекомендовал ему не упоминать об этом во время экзамена и церемонии посвящения.

Гедель обещал вести себя примерно, но не сдержал слова.

Когда чиновник, обращаясь к нему, сказал:

- До сего дня вы были подданным Германии…

Ученый поправил его:

- Не Германии, а Австрии.

- Неважно, ‑ продолжил чиновник. – В любом случае вы жили под гнетом чудовищной диктатуры, которая, к счастью, невозможна в нашей стране.

- Как раз наоборот! – воскликнул Гедель. – Я берусь доказать, что диктатура здесь возможна!

Друзьям стояло немало труда уговорить его воздержаться от этого не совсем уместного доказательства, а также убедить чиновников в необходимости для США в таком гениальном ученом.

 

Однако, через 2 года, в 1950 году, утверждение Геделя было доказано в общем виде другим математиком и экономистом – Кеннетом Эрроу ‑ в его докторской диссертации. Результаты диссертационного исследования К.Эрроу опубликовал в книге «Социальный выбор и индивидуальные ценности» («Social Choise and individual Values», K. Arrow). Это исследование в дальнейшем получило название «теорема о невозможности».

К. Эрроу поставил перед собой простую и одновременно великую цель: решить проблему рационального согласования индивидуальных интересов – найти некое правило, способ выбора одного из многих альтернативных решений – процедуру выявления воли народа да и вообще, любого сообщества – будь то совет директоров какой-нибудь фирмы, суд присяжных или общее собрание гаражно-строительного кооператива.

Он обратился к исследованию давно известной человечеству процедуры – принятию решений большинством голосов. В числе достоинств этой процедуры – простота, равноправие и весомость, обусловленная традицией.

Как должно быть устроено правило общественного выбора?

К. Эрроу выдвинул аксиомы, которым должна удовлетворять любая процедура комбинирования или объединения индивидуальных предпочтений, чтобы образовать коллективное суждение. То есть, он впервые провел аксиоматическое исследование рациональных процедур голосования и использовал этот подход к синтезу процедур голосования. Это направление синтеза переросло в сравнительный анализ процедур голосования, т.е. в выяснение того, в какой мере та или иная процедура удовлетворяет некоторому набору условий и критериев.

Действительно, существует бесконечное множество рациональных процедур голосования, и анализ каждой из них по отдельности задача невыполнимая. процедуры объединения индивидуальных предпочтений, в коллективное закрепляются законодательно на уровне Конституции государства. Поэтому требования сформулированы по отношению к Конституциям.

Итак,

 

Аксиомы Эрроу

Первая аксиома Эрроу. Универсальность.

Она требует, чтобы Конституция отражала каждую возможную конфигурацию предпочтений голосующих. Общество не должно принимать Конституцию, которая может оказаться несостоятельной хотя бы в некоторых структурах предпочтений голосующих. Следовательно, Конституция должна быть общей, чтобы разрешить все возможные споры.

Вторая аксиома Эрроу. Единогласия.

Она управляет действием Конституции, когда нет согласия между избирателями. Для конфигурации предпочтений, при которой каждый индивидуум считает, что , коллективное предпочтение должно быть таким же.

Третья аксиома Эрроу. Независимость.

Коллективное предпочтение любой пары альтернатив зависит только от предпочтений голосующих, касающихся этих альтернатив. Как бы не менялись индивидуальные предпочтения других альтернатив, если каждое из индивидуальных предпочтений альтернатив и остается неизменным, то и коллективное предпочтение альтернатив и не меняется.

Введем обозначения:

- отношение индивидуального предпочтения: означиет, что альтернатива предпочтительнее альтернативы ;

- отношение слабого коллективного предпочтения: 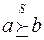означиет, что альтернатива не хуже альтернативы в смысле коллективного предпочтения;

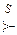- отношение сильного коллективного предпочтения: 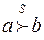означиет, что альтернатива предпочтительнее альтернативы в смысле коллективного предпочтения.

Четвертая аксиома Эрроу. Полноты.

Для каждой пары альтернатив должно выполняться либо 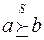или или и первое и второе одновременно (в этом случае альтернативы и ‑ безразличны в смысле коллективного предпочтения.).

Пятая аксиома Эрроу. Транзитивности.

Слабое коллективное предпочтение () должно быть транзитивно, т.е. если 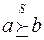и , то .

Но Эрроу требует транзитивности и для отношения строгого коллективного (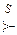) предпочтения: если 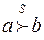и , то .

Примеры транзитивных отношений - сравнение действительных чисел.

Но, например, отношение «быть знакомым» не является транзитивным.

Если конституция является 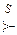-транзитивной и при этом удовлетворяет остальным аксиомам Эрроу, то такая конституция является нейтральной, т.е. если из частной конфигурации упорядочения альтернатив 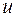и следует, что коллективно предпочитается , то из той же конфигурации предпочтений и следует, что коллективно предпочитается альтернатива .

 

К. Эрроу ввел, на первый взгляд, очевидные требования, которым должно удовлетворять правило голосования. Попробуем определить функцию коллективного предпочтения, которая будет удовлетворять этим требованиям.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: