Функция коллективного предпочтения.

 

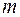Имеется избирателей и кандидатов. Нужно построить функцию, которая определяет коллективный порядок на множестве кандидатов, т.е. правило, которое для любых заданных порядков , ,…, определяет коллективный порядок

Таких функций может существовать много. например, функция может объявлять всех кандидатов равными. Но толку от такой функции – никакого.

Наложим некоторые ограничения на функцию :

1) определена для любого конечного числа кандидатов (например, для либо первый лучше, либо второй кандидат лучше, либо оба равны), т.е. удовлетворяет аксиоме полноты.

 

Определение 1. Дано: ‑ множество избирателей и подмножество из 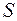: , называемое коалицией, причем . Коалиция называется -решающей для кандидата против кандидата тогда и только тогда, когда из того, что для всех избирателей из справедливо соотношение и для всех избирателей из справедливо противоположное соотношение следует что . Обозначают это так: .

Функция определяет порядок типа .

Коалиция зависит от конкретных кандидатов и и не обязана быть -решающей для кандидата против кандидата .

 

Определение 2. Если для любых двух кандидатов 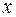и коалиция является -решающей для кандидата 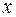против кандидата , то такая коалиция называется -решающей.

‑ Является ли множество всех избирателей -решающей коалицией?

‑ Почему?

‑ Может ли пустое множество быть -решающей для кандидата против кандидата ?

‑ Почему?

Лемма 1. Существует пара кандидатов , такая что существует коалиция, состоящая из одного избирателя , которая является -решающей для кандидата против кандидата .

Доказательство. Пусть ‑ множество таких коалиций 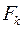б для каждой из которых существует пара кандидатов , что 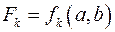(для каждой коалиции из эта пара кандидатов своя). Множество 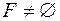, так как , то есть включает в себя и множество всех избирателей.

Возьмем коалицию из , которая содержит наименьшее число избирателей.

.

Так как 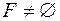, то содержит не менее одного избирателя ‑ .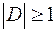

Докажем, что содержит ровно одного избирателя ‑ .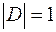

Предположим, что можно разбить на два непересекающихся непустых подмножества: одно - из одного избирателя, другое ‑ ‑ из всех остальных ‑ . Тогда всего получается 3 группы избирателей:

группа избирателей
кандидаты	a	c	b
b	a	c
c	b	a

 

Так как коалиция является - решающей для кандидата против кандидата , то .

Если , то коалиция является - решающей для кандидата против кандидата . Но в меньше избирателей, чем в , которая по определению минимальна. Следовательно, не может быть не хуже, чем .

Тогда, в силу аксиомы полноты, лучше, чем .

Теперь мы имеем, что и . Тогда по аксиоме транзитивности . А это означает, что является - решающей для кандидата против кандидата , что также противоречит минимальности коалиции .

Мы пришли к противоречию. Лемма доказана. ▄

Лемма 2. Коалиция (существование которой доказано в лемме 1) является -решающей.

Доказательство. Пусть ‑ произвольный кандидат. Рассмотрим профиль голосования:

группа избирателей
кандидаты	…	…
a	b
…	…
b	c
…	…
c	a
…	…

Избиратель считает, что и , а все остальные считают, что и .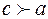

Так как является - решающей для кандидата против кандидата , то . И мы имеем, что для всех избирателей - по аксиоме единогласия. Следовательно, по аксиоме транзитивности и этот результат не зависит от по аксиоме независимости. Следовательно, является - решающей для кандидата против кандидата , то есть 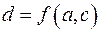, где - произвольный кандидат.

Проведя аналогичные рассуждения для произвольного кандидата в рассматриваемом профиле голосования:

группа избирателей
кандидаты	…	…
e	c
…	…
a	e
…	…
c	a
…	…

мы видим, что 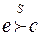, и получаем, что для произвольных кандидатов и . то есть, является - решающей. ▄

Лемма 3. Избиратель может навязывать свое мнение по поводу любых двух кандидатов и при условии, что мнение всех остальных избирателей противоположно.

В формулировке леммы 3 пока проявляется зависимость мнения диктатора от мнения других – его мнение не такое, как у всех остальных.

Доказательство. Докажем, что как бы ни голосовали остальные избиратели, коллективное мнение будет совпадать с мнением кандидата .

Рассмотрим такие профили голосования, в которых у избирателя порядок вида:

и все остальные избиратели ставят 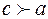и , а в остальном их расположение кандидатов произвольно.

Так как является - решающей, то 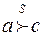. Для всех избирателей , следовательно, в силу аксиомы единогласия .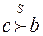

Тогда, по аксиоме транзитивности, получаем, .

Исключая из соотношений кандидата (по аксиоме независимости), получаем, что если избиратель считает, что кандидат лучше, чем кандидат (), то ему будет оказано коллективное предпочтение .

То есть из следует . это означает, что порядок предпочтений у избирателя и коллективного мнения совпадает.

Следовательно, если , то .

Таким образом, . ▄

Лемма 3 показывает, что единственный кандидат может диктовать свои предпочтения коллективу избирателей. То есть этот кандидат является ДИКТАТОРОМ!

Таким образом, получаем неожиданный результат: при всей разумности выдвигаемых требований к процедурам голосования, имеется только одна, удовлетворяющая всем пяти аксиомам – это правило диктатора.: независимо от предпочтения других избирателей, она устанавливает тот коллективный порядок, который определяется первым избирателем (вместо первого может быть второй или третий – не имеет значения).

Диктатор – это личность, обладающая властью навязывать обществу свое строгое предпочтение для произвольной пары альтернатив.

Роль диктатора может выполнять, например, партия или религия, угроза большой войны, авторитет влиятельного меньшинства – аксакалы и пр.

Получается, что для решения «тупиков демократии» требуется внешнее давление на общество, которое лишает избирателей хотя бы части их вожделенной свободы!

К. Эрроу, будучи искренним приверженцем демократии и гражданином США, не мог объявить такой результат на весь мир. и он добавил шестую аксиому.

Шестая аксиома Эрроу. Отсутствие диктатуры.

Теперь в совокупности уже шесть аксиом являются противоречивыми. шестая аксиома исключает существование единственной процедуры, которая удовлетворяет первым пяти. Окончательный вывод Эрой сформулировал в виде теоремы:

Теорема о невозможности. Не существует правила, объединяющего индивидуальные предпочтения в коллективное, которое удовлетворяет всем шести аксиомам.

 

В теченее последних лет ученые не переставали исследовать аксиомы Эрроу в попытке обойти его теорему о невозможности, стремясь ослабить сформулированные им требования.

Отказ от аксиом универсальности и независимости не пролил свет на реальные механизмы выбора. Ряд попыток исследовать другие аспекты механизмов выбора при общих предположениях также привели к отрицательным результатам. В частности было известно, что в процессах коллективного выбора участники могут добиваться лучших для себя исходов, давая ложную информацию о своих предпочтениях, и возникла проблема: построить механизм, который был бы неманипулируем, то есть делал бы дезинформацию невыгодной. В 1973 г. Гиббaрд [10] доказал, что универсальных неманипулируемых и не диктаторских механизмов не существует. Один из основных методологических постулатов теории социального выбора, состоит в том, что долговременно действующие механизмы должны быть наилучшими из возможных. Этот постулат базируется на дарвинистском представлении о естественном отборе. Благодаря ему грань между нормативной и дескриптивной теорией оказывается размытой, проблема сводится к правильной формулировке понятия оптимальности. Постулат оптимальности нашел впечатляющее (хотя лишь частичное) подтверждение в теории экономического равновесия, но, видимо, не оправдал себя в теории социального выбора. Ответ на основной вопрос: "Чем выделены механизмы, действующие в реальности?" так и не был получен.

Эта проблема вызывает широкий интерес, т.к. она тесно связано с ключевыми вопросами экономики, философии, общественных наук.

Таким образом, нельзя синтезировать идеальную систему голосования не потому что фантазии не хватает, а потому, что ее не может быть. Рациональный общественный выбор не может быть компромиссным!

В частности за эту работу К. Эрроу в 1972 году получил Нобелевскую премию.

Вывод К. Эрроу определяет ограничения на правила коллективного принятия решений: три общепризнанные цели – коллективная рациональность, способность принимать решения и равенство власти оказываются в непримиримом противоречии!

Если общество отказывается от коллективной рациональности, тем самым принимая необходимую произвольность и возможность оказывать влияние на нерациональные процедуры, то принцип большинства обеспечит выбор, так как с его помощью можно достичь две другие цели.

Если общество настаивает на сохранении некоторой степени коллективной рациональности, то оно может достичь равенства, приняв правило консенсуса, но только ценой крайней нерешительности.

Общество может увеличить способность принимать решения, концентрируя право вето во все более узком кругу индивидуумов.

 

Исследования К. Эрроу привели к более глубокому пониманию существующих методов голосования и, возможно, помогут создать более совершенные. Но возможности строго ограничены и решительные компромиссы неизбежны.

 

Выбор процедуры голосования является сложной проблемой, включающей в себя философские, мировоззренческие, психологические и технические аспекты, и как мы уже говорили, носит принципиальный характер. Но при этом нужно знать:

‑ является ли кандидатами люди или технические проекты

‑ насколько хорошо избиратели хорошо знают кандидатов

‑ может ли избиратель воздержаться в голосовании.

‑ каковы технические возможности обработки результатов голосования

‑ что считать большинством ‑ когда выборы считаются состоявшимися

‑ всегда ли можно решать вопросы голосованием.

(А.И. Герцен «Что, если бы Колумб или Коперник пустили Америку и движение Земли на голоса?»)

 

Литература

1. Вольский В.И. Турнирные функции в задачах коллективного и многокритериального выбора. Исследования по теории структур. / В.И. Вольский. ‑ М.: Наука, 1987 ‑ ___ с.

2. Вольский В.И., Лезина З.М. Голосование в малых группах. Процедуры и методы сравнительного анализа. / В.И. Вольский, З.М. Лезина. ‑ М: Наука, 1991. ‑ ___ с.

3. Воробьев Н.Н. Теория игр для экономистов-кибернетиков. / Н.Н. Воробьев. ‑ М.: Наука, 1985. ‑ ___ с.

4. Ларичев О.Н. Наука и искусство принятия решений. / О.Н. Ларичев. ‑ М.: Наука, 1979. ‑ ___ с.

5. Маркин Б.Г. Проблема группового выбора. / Б.Г. Маркин ‑ М.: Наука, 1974. ‑ ___с.

6. Моисеев Н.Н. Математика - управление - экономика. / Н.Н. Моисеев. ‑ М.: Знание, 1970. ‑ ___ с.

7. Мулен Э. Кооперативное принятие решений: Аксиомы и модели. / Э. Мулен. ‑ М.: Мир, 1991. ‑ ___ с.

8. Arrow K. J. Social Choice and Individual Values. / K. J. Arrow. ‑ New York: Wiley, 1951. ‑ __ p.

9. Gibbard A. Manipulation of voting schemes: A general result. / A. Gibbard. Econometrica – 1973 ‑ V. 41, 587 28.

 

 

Домашнее задание.

Для приведенных результатов голосования по известным правилам определить победителя среди 4 кандидатов:

.

Количество очков, получаемых кандидатом за соответствующее место, укажите самостоятельно. Здесь n- последняя цифра номера зачетной книжки, m – предпоследняя цифра.

 

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: