 |
Тема 5.1 Средние величины. Эталон ответа. Инструкция по выполнению задания № 1-6; соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву столбца 2, обозначающую правильный ответ на вопросы столбца 1
|
|
|
|
Тема 5. 1 Средние величины
| № п\п | Задание (вопрос) |
Эталон ответа | ||||
|
Инструкция по выполнению задания № 1-6; соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв. | ||||||
|
Установите соответствие между статистическими показателями и их определениями Показатели: 1). Абсолютные 2). Относительные 3). Средняя Определения: А. Величины, представляющие собой отношение одних статистических показателей к другим Б. Обобщающая величина статистической совокупности, выражающая типический уровень (характерный размер) признака у единиц изучаемой однородной совокупности. В. Характеризуют размеры, объемы, уровни явлений и процессов, получающиеся в результате статистического наблюдения и сводки исходной информации. | ||||||
|
Установите соответствие между структурными средними и их определениями Показатели: 1). Квантили 2). Квартили 3). Квинтили 4). Децили Определения; А. Показатели, которые делят ранжированный ряд на десять равных частей Б. Показатели, которые делят ранжированный ряд на пять равных частей В. Показатели, которые делят ранжированный ряд на четыре равные части Г. Показатели, которые делят вариационные ряды на определенное количество равных частей. | ||||||
| Соотнесите виды средних величин: 1) Степенные средние 2) Структурные средние Виды средних: А. Арифметическая Б. Квадратическая В. Медиана Г. Геометрическая
Д. Мода Е. Гармоническая Ж. Децили З. Квартили | ||||||
| Установите соответствие между видами степенных средними и условиями их применения: Виды средней: 1) Средняя арифметическая 2) Средняя гармоническая 3) средняя квадратическая. 4) средняя геометрическая Условия применения: А. При вычислении средних значений в рядах динамики для темпов роста, рассчитанных цепных способом Б. Исчисляется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой совокупности В. Рассчитывается тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, представлена как их произведение Г. Используется для анализа вариации признака в вариационном ряду | ||||||
| Соотнесите формулы: 1. 2. 3. 4. | ||||||
| Соотнесите формулы: 1. 2. 3. 4.
| ||||||
| Инструкция по выполнению заданий 7-16: Выберите букву, соответствующую правильному варианту ответа и запишите ее в бланке ответов. | ||||||
|
, где — значение осредняемого признака а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная
ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешенная | ||||||
|
значение осредняемого признака - частота а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешенная | ||||||
| а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешенная | ||||||
|
где веса осредняемого признака отдельные значения осредняемого признака а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешеннаясредняя арифметическая невзвешенная | ||||||
| Формула а) средняя арифметическая б) средняя гармоническая в) мода г) медиана ж) средняя квадратическая е) средняя геометрическая | ||||||
| Формула а) средняя арифметическая б) средняя гармоническая в) мода г) медиана ж) среднее квадратическая е) средняя геометрическая | ||||||
| Формула а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная
г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешенная | ||||||
| Формула а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешенная | ||||||
| Формула а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешенная | ||||||
| Формула а) средняя арифметическая невзвешенная б) средняя арифметическая взвешенная в) средняя гармоническая невзвешенная г) средняя гармоническая взвешенная д) средняя геометрическая невзвешенная е) средняя геометрическая взвешенная ж) средняя квадратическая невзвешенная з) средняя квадратическая взвешенная | ||||||
|
Инструкция по выполнению заданий 17-20: В соответствующую строку бланка ответов запишите краткий ответ на вопрос, окончание предложения или пропущенные слова | ||||||
|
Обобщающая величина статистической совокупности, выражающая типический уровень изучаемого признака, называется | ||||||
|
Величина, которая делит статистическую совокупность на 2 равные части | ||||||
|
Средняя величина, характеризующаяся чаще всего встречающейся вариантой, называется
| ||||||
|
Правило мажорантности | ||||||
. 
А. Средняя квадратическая
Б. Средняя геометрическая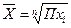
В. Средняя арифметическая
Г. Средняя гармоническая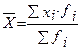
А. Средняя квадратическая
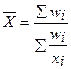Б. Средняя геометрическая
В. Средняя арифметическая
Г. Средняя гармоническая
|
|
|
