Симплекс-метод решения ЗЛП.

В основе геометрической интерпретации решения системы m линейных уравнений с n неизвестными (m<n) лежит теорема: каждому допустимому базисному решению системы ограничений ЗЛП соответствует угловая точка многоугольника решений. Справедлива и обратная теорема: каждой угловой точке множества допустимых решений системы ограничений (многоугольника решений) соответствует допустимое базисное решение. Обобщая упомянутые в этом параграфе теоремы можно сформулировать следствия: если существуют, и при том единственное оптимальное решение задачи линейного программирования, то оно совпадает с одним из допустимых базисных решений системы ограничений.

Очевидно, число допустимых базисных решений конечно и не превышает . Следовательно, для случая, когда число переменных не позволяет решить задачу графически, или это решение представляет технические сложности, можно решить задачу так: найти все допустимые базисные решения системы ограничений, вычислить значение целевой функции выбрать наибольшее и наименьшее. Однако, практическое осуществление столь «прозрачного» метода связано с большими вычислительными трудностями.

Число перебираемых допустимых базисных решений можно значительно сократить, если производить перебор не беспорядочно, а с учетом изменения целевой функции, добиваясь, чтобы каждое следующее решение было «лучше» или, по крайней мере «не хуже», чем предыдущее, то есть увеличивалось при отыскании максимума, и уменьшалось при отыскании минимума. Идея последовательного улучшения легла в основу универсального метода решения ЗЛП – симплекс-метода.

Впервые симплексный метод решения был предложен американским ученым Дж.Данцигом в 1949 году, хотя еще в 1939 году его идеи были разработаны советским ученым Л.В. Канторовичем. На основе симплекс метода создан пакет прикладных программ 1рх88, обладающий достаточно большими вычислительными возможностями. Однако, студентом необходимо ознакомиться с сутью этого метода, которую мы изложим на примере.

Симплекс-метод изложим для ЗЛП, поставленной в канонической форме: f→min, ограничения в виде системы уравнений, число переменных любое.

Пример. Решить симплекс-методом задачу:

F=4-x₂+x₅→min;

 

1. Проверим, является ли система уравнений совместной. Для этого найдем ранг матрицы и ранг расширенной матрицы:

; r()=r()=3.

2. Построим какое-либо исходное допустимое базисное решение системы ограничений задачи. В качестве базисных выбираем те три переменные, при который определитель 3 порядка не равен нулю и содержит больше нулей и единиц. Выразим целевую функцию через свободные переменные.

1 этап: х₁,х₃,х₄ – базисные, х₂,х₅ – свободные;

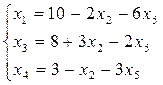
Проверим, является ли построенное базисное решение допустимым, то есть выполняются ли неравенства X_j≥0. Если решения не является допустимым, в качестве базисных выбираем три другие переменные, при которых определитель не равен нулю.

3. Поставим вопрос – можно ли каким либо образом «улучшить» решение? Легко понять, что функцию можно уменьшить за счёт увеличения любой свободной переменной, входящей в выражение целевой функции с отрицательным коэффициентом. Это можно осуществить, перейдя к такому новому допустимому базисному решению, в котором эта переменная станет базисной и примет не нулевое, а положительное значение. Формальным признаком выбором такой переменной является знак «минус» перед свободной переменной в выражении целевой функции. В нашем случае это переменная х_2.

Однако, базисных переменных должно быть на каждом этапе решения задачи ровно 3, т.к. r=3. Чем больше будет значение переменной, тем меньше будет значение целевой функции, но система ограничений накладывает условия на рост переменной x₂.

Поскольку необходимо сохранить допустимость решений, т.е. все переменные должны остаться неотрицательными, то должны выполняться следующие неравенства (x₅=0 как свободная переменная):

Формально оценочные отношения для x₂ можно получить, составляя для каждого уравнения системы ограничения отношение свободного члена к коэффициенту при меняемой переменной, если меняемая переменная входит в выражение целевой функции со знаком «-»; если меняемая переменная не входит в уравнение или входит с положительным кооэффициентом, то это отношение заменяем символом ~. Очевидно, что сохранение неотрицательности всех переменных решения возможно, если не нарушается ни одна из полученных во всех уравнениях границ. В данном примере наибольшее возможное значение для переменной x₂ определяется как x₂=min{5,~,3}=3. При x₂= 3 переменная x₄ обращается в нуль и переходит в свободные.

Уравнение, где достигается наибольшее возможное значение переменной, переводимой в базисные (т.е., где оценка минимальна), называется разрешающим. В данном случае – это третье уравнение. Разрешающее уравнение будем выделять рамкой в системе ограничений.

4. Решая последнее разрешающее уравнение, находим меняемую переменную х₂ и подставляем ее в оставшиеся ограничения и в выра­жение целевой функции. Находим тем самым новое допустимое базис­ное решение.

2 этап: X₁, х₂, х₃ - базисные, х₄, х₅ - свободные;

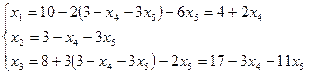
Проверяем можно ли "улучшить" решение, т.е. имеются ли в выраже­нии целевой функции свободные переменные с отрицательными коэффициентами. В нашем случае таковых нет. Задача решена, построенное решение оптимально.

Ответ: f_min = 1, .

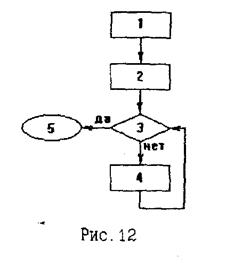Блок-схема симплекс-метода.

1. Постановка задачи в канонической форме. Построение исходного допустимого базисного решения.

2. Проверка критерия оптимальности. Если все свободные пере­менные входят в выражение целевой функции с положительными коэф­фициентами, то построенное решение оптимально, переходим к пункту
5; если критерий оптимальности не выполнен, то переходим к пункту
4.

3. Построение нового допустимого базисного решения.

4. Конец.

Доказано, что за конечное число шагов можно получить оптимальное решение.

 

Частный случай 1. Если на каком-то этапе решения ЗЛП в выра­жении целевой функции имеется свободная переменная с отрицатель­ным коэффициентом, а во все уравнения системы ограничений она ли­бо не входит, либо входит с положительным коэффициентом, то целевая функция не ограничена при данной системе ограничений. Опти­мального решения нет.

Частный случай 2. Если при переходе к оптимальному решению на последнем этапе симплекс-метода в выражении целевой функции исчезает хотя бы одна из свободных переменных, то полученное оп­тимальное решение не единственное. Чтобы получить другое решение, нужно сделать еще один шаг симплекс-метода и перевести в базисные исчезнувшую переменную.

 

4. ТРАНСПОРТНАЯ ЗАДАЧА ПО КРИТЕРИЮ СТОИМОСТИ И ЕЕ РЕШЕНИЕ.

Постановка ТЗ.

В главе 1 была дана постановка ТЗ по критерию стоимости, для
двух поставщиков и трех потребителей. Обобщая эту задачу на m
поставщиков и п потребителей, получим следующую математическую
постановку ТЗ:

ТЗ представляет собой задачу линейного программирования с числом переменных m*n и числом ограничений равенств m + n. Усло­вие (23) гарантирует полный вывоз груза из всех пунктов отправле­ния, а условие (24) означает полное удовлетворение спроса.

Если

то ТЗ называется задачей с правильным балансом или закрытой задачей, в противном случае ТЗ называется задачей с неправильным ба­лансом или открытой задачей.

Равенство (26) является необходимым и достаточным условием совместности системы уравнений (24), (25) в области допустимых решений и, следовательно, разрешимости задачи.

Рассмотрим закрытую ТЗ. Эта задача может быть решена симп­лекс-методом, как любая ЗЛП. Однако, специфичная форма системы ограничений данной задачи позволяет существенно упростить обычный симплекс-метод и разработать более эффективные вычислительные методы. Модификация симплекс-метода применительно к ТЗ называется распределительным методом.

Некоторые определения и теоремы:

Определение. Набор переменных {x_ij}, удовлетворяющих условиям (23) - (25), записывается в виде матрицы:

Матрица называется планом перевозок, а переменные х_ij - перевозками.

Определение. Всякое неотрицательное базисное решение системы линейных уравнений (23), (24), определяемое матрицей , называет­ся опорным планом ТЗ.

Определение. Опорный план , при котором функция (22) при­нимает свое минимальное значение, называется оптимальным опорным планом или просто оптимальным планом ТЗ.

Определение. Матрица, составленная из стоимостей на перевоз­ку единицы груза от i-го поставщика к j-му потребителю, называет­ся матрицей стоимостей (матрицей коэффициентов затрат, матрицей тарифов, матрицей транспортных издержек).

Определение. Таблица, составленная из мощностей поставщиков и потребителей, а также из коэффициентов затрат, называется таб­лицей поставок или таблицей перевозок (коэффициенты затрат ста­вятся в левом верхнем углу соответствующей клетки таблицы).

Подобно тому, как это было в симплекс-методе, в распредели­тельном методе решение ТЗ состоит из следующих основных этапов:

- определение исходного допустимого базисного решения задачи
(первоначального распределения поставок, первоначального опорного
плана);

- оценка этого плана по критерию стоимости:

- переход к следующему, "лучшему" плану путем замены одной
из базисных переменных на свободную.

-

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: