 |
Распределительный метод решения ТЗ
|
|
|
|
1. Проверяем, является ли ТЗ задачей с правильным балансом.
2. Находим исходное допустимое базисное решение ТЗ методом СЗУ или МНС.
3. Рассматриваем все свободные клетки таблицы перевозок,составляем для них циклы пересчета и находим оценки свободных клеток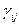 
. Выбираем ту клетку, которая имеет наибольшую по моду-
лю отрицательную оценку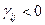 
.
4. Производим сдвиг по циклу пересчета этой свободной клетки. Получаем новую таблицу перевозок.
5. Операции 3, 4 повторяем до тех пор, пока для всех свободных клеток не будет выполняться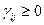 
.
Пример. Построить оптимальное решение ТЗ. исходное допустимое решение которой, построенное методом СЗУ, задано в таблице 5.
Решение. Проверяем выполнение критерия оптимальности, начиная с первой строки:
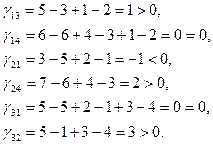
Единственная свободная клетка с номером (2,1) имеет отрицательную оценку. Проводим сдвиг по циклу на число e, где e =min (40,60) = 40. После сдвига по циклу базисная клетка (1, 1) станет свободной (х11 = О), свободная клетка (2,1) станет базисной со значением х21 = 40. В соответствии с определением операции сдвига по циклу на число e = 40: х12 = 60. х22 = 20 (табл. 7).
Таблица 7
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | B4 | запасы |
| A1 | 5 40 | 2 20 | 5 | 6 | ||
| A2 | 3 | 1 60 | 3 20 | 7 | ||
| A3 | 5 | 5 | 4 30 | 6 40 | ||
| потребности |
В результате получаем новую таблицу перевозок (табл. 8)
Таблица8
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | B4 | запасы |
| A1 | 5 | 2 60 | 5 | 6 | ||
| A2 | 3 40 | 1 20 | 3 20 | 7 | ||
| A3 | 5 | 5 | 4 30 | 6 40 | ||
| потребности |
Проверяем справедливость критерия оптимальности для данного распределения поставок:
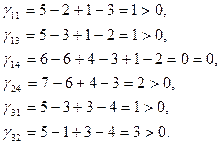
Итак, для всех свободных клеток имеем. Следовательно, распределение поставок оптимально.
|
|
|
Ответ:
.
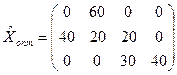fmin=2*60 + 3*40 + 1*20 + 3*20 + 4*30 + 6*40 = 680.
Замечания о выборе числа e, на которое производится
сдвиг по циклу пересчета свободной клетки
1. По определению e= min(из значений хij в отрицательных вершинах цикла пересчета данной свободной клетки).
2. Может оказаться, что e = О. В этом случае значения поставок в вершинах цикла не изменяются, значение целевой Функции при переходе к новому решению не изменяется, но бывшая свободная
клетка станет базисной с нулевой поставкой.
3. Может случиться, что минимум достигается одновременно для нескольких значений, стоящих в отрицательных клетках. После сдвига по циклу в этих клетках будут нулевые поставки. Однако, свободной считаем только одну из этих клеток. остальные считаются базисными с нулевыми поставками.
4.5. ТЗ по критерию стоимости с неправильным балансом
Задача с неправильным балансом сводится к задаче с правильным балансом путем введения так называемых фиктивныхпунктов от правления и фиктивныхпунктов назначения.
Случай 1. Пусть
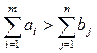
то есть суммарная мощность поставщиков больше суммарной мощности потребителей.
Вводим фиктивный пункт назначения Bn+1. потребности в грузе
которого составляют
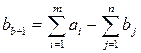
Стоимости перевозок из всех пунктов отправления в фиктивный пункт назначения Bn+1 полагаем равными нулю: c1n+1, c2n+1, … cmn+1=0.
Получим ТЗ с правильным балансом:
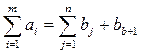
Пример. Найти оптимальное распределение поставок для Т3, заданной таблицей 11.
Таблица 11
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | запасы |
| A1 | 1 | 3 | 2 | ||
| A2 | 2 | 1 | 3 | ||
| потребности |
Решить задачу самостоятельно.
Ответ.
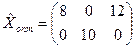, fmin=42.
Из пункта А2 будет отправлено 5 единиц груза.
Случай 2. Пусть
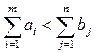
Вводим фиктивный пункт отправления Am+1, запас груза в котором:
,
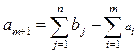Стоимости перевозок из фиктивного пунктa отправления Am+1 во все пункты назначения полагаем равными нулю: c1m+1, c2m+1, … cm+1n=0.
|
|
|
Получим ТЗ с правильным балансом:
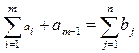
Пример. Найти оптимальное распределение поставок для ТЗ, заданной таблицей 12.
таблица 12.
| Пункт отправления | Пункт назначения | B1 | B2 | B3 | запасы | |
| A1 | 3 | 1 | 5 | 2 | ||
| A2 | 4 | 6 | 7 | 3 | ||
| A3 | 2 | 8 | 4 | 5 | ||
| потребности |
Задачу решить самостоятельно.
Ответ.
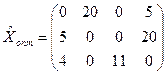, fmin=162.
Потребности пункта B3 будут не удовлетворены на 5 единиц.
Замечание. При нахождении исходного решения ТЗ с неправильным балансом МНС следует фиктивные пункты учитывать в самую последнюю очередь, то есть выбирать наименьшую стоимость в первую очередь среди стоимостей реальных пунктов.
Внимание к ТЗ обусловлено тем, что задачи подобного типа и многие другие ЗЛП, во-первых, часто встречаются в практических расчётах, и, во-вторых, к ним сводятся многие другие задачи линейного программирования: сетевая задача, задача о назначениях, задача календарного планирования.
|
|
|
