 |
Доли и дроби в курсе математики начальных класса
|
|
|
|
Лекция 18.Система изучения дробей в начальной школе
1. Понятие дроби.
2. Дроби (доли) в 3 классе.
3. Дроби в 4 классе.
4. Дроби величин.
Понятие дроби
Темы «Доли» и «Дроби» традиционно присутствовали во всех учебниках по математике для начальных классов. В прежних вариантах учебников тема «Доли» рассматривалась во 2 классе системы 1—3 и в 3 классе системы 1—4. Дети знакомились с понятием доли (дроби вида х/к) и дроби (правильной дроби, в которой числитель меньше знаменателя), учились сравнивать дроби с опорой на предметную модель и решать два вида задач с дробями: нахождение дроби от числа и нахождение числа по его дроби.
На сегодня в соответствии с Обязательным минимумом требований к уровню подготовки выпускников начальной школы объем изучения данной темы значительно сократился в учебниках традиционной содержательной ориентации (учебники М.И. Моро и др., учебники Н.Б. Истоминой). В то же время эта тема значительно расширена в альтернативных учебниках системы Л.В. Занкова, системы В.В. Давыдова и «Школы 2100». В этих методических школах расширение объема знакомства с дробями обусловлено стремлением авторов сформировать у ребенка более общее представление о числе. Поскольку сформировать хоть в какой-то мере обобщенное представление об объекте возможно только в процессе произведения умственных операций над данным объектом (сравнение его с объектами другого рода, выделение сходства и различия, проведение аналогий и др.), необходимо иметь для организации данной умственной деятельности хотя бы два вида объектов. Знакомство младших школьников только с натуральными числами не позволяет проводить такую работу. Дроби не являются натуральными числами (поскольку не являются целыми) — это числа рациональные. Не ввода в словарь ребенка эти термины, можно тем не менее организовать работу по сопоставлению этих двух видов чисел и знакомству с некоторыми сходными операциями с этими числами (соотнесение с предметной моделью, запись, сравнение, сложение и вычитание дробей с одинаковыми знаменателями и т. п.).
|
|
|
В последней редакции традиционного учебника математики понятие «Доля целого» рассматривается в 4 классе (часть 1) и некоторые сведения о дробях даются на последних страницах учебника для 4 класса (часть 2). Задания на нахождение дроби величин и величины по ее дроби встречаются в тексте учебных пособий несколько раз. Мы полагаем, что данная редакция учебника не является последней, поэтому в настоящем учебном пособии даем материал по данной теме в соответствии с традиционным объемом ее изучения в начальных классах и даже чуть шире — для того, чтобы подготовить студентов для работы по альтернативным программам.
Понятие дроби связано с расширением множества целых чисел до множества рациональных чисел. Теоретически считается, что знакомство младших школьников с долями и дробями имеет целью расширение их представлений о числе, однако, практически этого не происходит, поскольку понятие дроби в том виде, в каком оно всегда рассматривалось в начальной школе, с множеством чисел фактически не связывается.
Дробь в классической методической трактовке курса математики для начальных классов — это скорее способ получения части объекта, при этом искомая часть необходимо удовлетворяет ряду специальных требований.
В математике рассматривается два подхода к определению понятия дроби — аксиоматический (через словесное определение и описание свойств) и практический — на основе измерения длин отрезков.
По определению дробь — это число вида  , где тип — целые числа, причем п не равно 0.
, где тип — целые числа, причем п не равно 0.
|
|
|
Далее определяется ряд операций для чисел этого вида (что понимать под сложением и вычитанием дробей, что понимать под умножением и делением дробей, какую дробь считать большей, а какую — меньшей) и ряд свойств, которыми обладают дроби (например, основное свойство дроби: числитель и знаменатель можно умножить или разделить на одно и то же число, при этом значение дроби не изменится).
Такой подход отражен в учебниках для 5—6 классов, что позволяет говорить о возможности формирования понятия дроби как числа.
В учебниках математики для начальных классов отражен другой подход к определению понятия рационального числа (дроби) — через измерение длины отрезка. Для описания результата этого процесса используют дробь.
Суть процесса состоит в следующем: если удается разделить некоторый объект А (например, отрезок) на b равных частей (т. е. взятую мерку b уложить по длине отрезка без остатка) и взять с таких частей, то, результат этой операции можно выразить так:
Получена  часть объекта А. При этом
часть объекта А. При этом  не рассматривается как самостоятельное число, а только как «
не рассматривается как самостоятельное число, а только как « - ая часть объекта А».
- ая часть объекта А».
Например, для ученика начальных классов фактически не имеет смысла символ 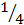 сам по себе, так как непонятно, что именно разделено на 4 равные части. В то же время словосочетание «
сам по себе, так как непонятно, что именно разделено на 4 равные части. В то же время словосочетание «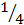 часть яблока» имеет смысл: из него ребенку ясно, что яблоко было разделено на 4 равные части и взята 1 часть.
часть яблока» имеет смысл: из него ребенку ясно, что яблоко было разделено на 4 равные части и взята 1 часть.
Таким образом, программой начальных классов не предусмотрено формирование понятия дроби как числа. Сведения о дробях ребенок получает только через практические действия над реальными объектами, величинами, множествами и описание этих действий на языке специальных символов (дробей). Все эти действия считаются подготовкой к знакомству с дробями в 5—6 классе. Данный подход к формированию представлений о долях и дробях реализован во всех альтернативных учебниках математики для начальных классов.
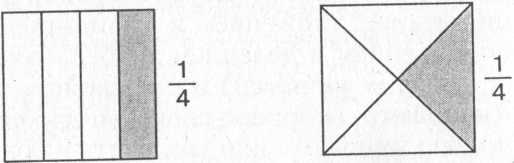
Методическая проблема знакомства ребенка с дробями состоит в выборе учителем целесообразного множества исходных объектов и практических операций, которые ученик будет выполнять над ними. Понятие дроби будет отождествляться с результатом этой операции. Термин «целесообразное множество» подразумевает, что множество выбранных объектов должно делиться нацело, иначе нельзя воплотить требование «равные части», при этом в случае геометрической фигуры можно иметь в виду и равновеликие части, например:
|
|
|


|
Сформированность представлений о дробях отражается в умении выполнять следующие операции:
1) записывать дробь, ориентируясь на объект или рисунок;
2) сравнивать дроби с опорой на объект или рисунок;
3) находить «дробь от числа» (делением объекта или множества на равные части);
4) восстанавливать число по известной его дроби (обратная операция).
Все эти умения формируются на основе принципа наглядности и неотрывности от предметного содержания.
Дроби (доли) в 3 классе
Словом «доля» в 3 классе называют дробь вида  . Долю получают делением объекта на несколько равных частей.
. Долю получают делением объекта на несколько равных частей.
Запись вида  ,
,  подразумевает, что объект разделили на две или четыре равных части и взяли одну из них. Запись такого вида в последней редакции учебника математики для 3 класса (2001) не рассматривается.
подразумевает, что объект разделили на две или четыре равных части и взяли одну из них. Запись такого вида в последней редакции учебника математики для 3 класса (2001) не рассматривается.
Детям сообщается словесное название полученной части: одна двенадцатая доля, одна шестая доля...
Используя рисунок круга, разделенного на несколько равных частей дети сравнивают доли, обозначая результат сравнения словом (а не знаком).
Например:
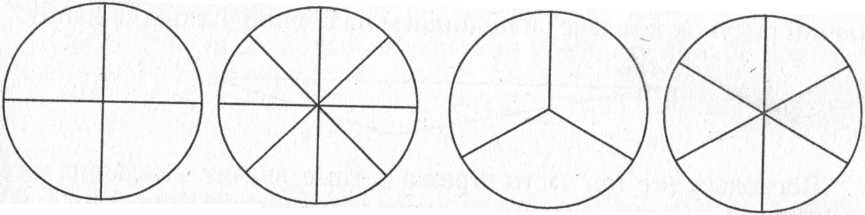
Назови, какие доли круга получились на каждом чертеже. Сравни, какая доля больше: одна восьмая или одна четвертая; одна третья или одна шестая.
Далее в учебнике сразу предлагаются задания на нахождение доли величины и величины по ее доле, сформулированные в виде задач.
Приведем пример задания на нахождение доли величины:
Длина ленты 9 дм. Отрезали одну треть этой ленты. Сколь-:о дециметров ленты отрезали?
Выполнение:
Данное задание является типовой задачей на нахождение доли величины. Смысл задания соответствует процессу нахождения доли объекта. Для иллюстрации этого смысла дети чертят в тетради отрезок длиной 9 дм (модель заданного в задаче объекта). Повторяют способ действия для получения одной третьей части (доли) объекта: разделим отрезок на три равные части. Запись 9 дм: 3 = 3 дм. Затем выполняют операцию разделения на отрезке и измеряют полученную третью часть (проверка).
|
|
|
Приведем пример задания (задачи) на нахождение числа по его доле:
Длина одной третьей части отрезка равна 4 см. Узнай длину всего отрезка.
Выполнение:
Данная задача является обратной по отношению к приведенной выше.
Для построения модели ситуации данной задачи следует рассуждать так. Нарисуем произвольный отрезок. Его длину мы не знаем. Обозначим ее знаком вопроса:

В задаче дана длина одной третьей части отрезка — разделим его на три равные части (приблизительно, поскольку это лишь рабочий рисунок к задаче) и подпишем над одной частью ее длину:
4 см

Поскольку все три части отрезка равные, значит, каждая из них должна иметь длину 4 см. Тогда длина всего отрезка 4 см • 3 = 12 см.
Далее в учебнике 3 класса (часть 2) встречаются задания этого же вида, в которых нужно найти доли (части) различных величин.
Например:
Квадратный лист бумаги со стороной 2 дм разрезали на пять равных частей прямоугольной формы. Найди площадь одной части.
Решение:
Задачу решают практическим способом, поскольку способы вычисления площади по формуле дети узнают в 4 классе.
В начальных классах школы учится 210 человек. Одну третью часть всех учеников составляют третьеклассники. Сколько детей учится в первых и вторых классах этой школы?
Решение:
Задачу решают, сопровождая ее наглядным изображением ситуации. Рассуждают так. Чтобы найти одну третью часть от всего количества детей, разделим его на 3:
?
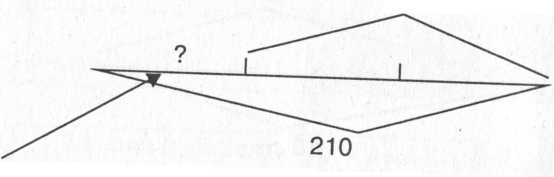
210: 3 = 70 (чел.) — это третьеклассники
На всех остальных детей приходится две части, значит 70 • 2 = - 140 (чел.).
Или по другому: все остальные дети учатся в 1 и 2 классе, значит, 210- 70= 140 (чел).
За полгода в районную библиотеку поступило 200 книг для детей. Это составляет четвертую часть всех поступивших книг. Сколько всего книг поступило в библиотеку за эти полгода?
Решение:
Задачу решают, сопровождая ее наглядным изображением ситуации. Рассуждают так:
Обозначим произвольным отрезком все поступившие книги — мы не знаем сколько их:

?
Известна четвертая часть всех книг – разделим отрезок на 4 равные части (приблизительно) и обозначим известную часть.
200 кн.

?
Поскольку все четыре части равны, значит, на каждую из них должно приходиться по 200 книг, значит, 200 • 4 = 800 (кн.) поступило в библиотеку.
Дроби в 4 классе
В 4 классе ставится задача нахождения нескольких долей целого. Например:
Длина отрезка 10 см. Он разделен на 5 равных частей. Сколько сантиметров в четырех пятых долях этого отрезка? Рассмотри чертеж и решение:
|
|
|
?

10 см
1) Найдем, сколько сантиметров в одной пятой доле отрезка: 10 см: 5 = 2 см.
2) Найдем, сколько сантиметров в четырех пятых долях отрезка:
2 см • 4 = 8 см. Ответ: 8 см.
Работа над данным понятием идет исключительно в словесных обозначениях: детям сообщается термин и дается его практическая иллюстрация. Символьное обозначение дроби на данном этапе не рассматривается.
Далее предлагаются различные задания (в виде задач на нахождение нескольких долей числа) аналогичного характера.
Например:
Начерти отрезок длиной 60 мм. Раздели его на 6 равных частей. Сколько миллиметров в пяти шестых долях этого отрезка?
В данном случае речь идет только о пяти долях из шести имеющихся, но не о дроби 5/6.
Знакомство с символикой и операция сравнения дробей рассматривается на последних страницах учебника математики для 4 класса (часть 2).
Рассматривается способ записи дроби: 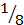 ; 5/6; 3/5.
; 5/6; 3/5.
Правильный способ чтения этой записи и смысл каждого ее элемента: число, записанное под чертой, показывает, на сколько равных частей разделено целое число; число, записанное над чертой, показывает, сколько взято таких частей.
Слова «числитель» и «знаменатель» детям не сообщаются.
Сравнение дробей проводится с опорой на рисунок. Следует обращать внимание на то, что необходимо сравнивать соизмеримые части одного объекта, поскольку для ученика начальной школы дроби — это только части объекта или множества.
Например:

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Что больше:  или
или  ?
?  или
или  ?
?  или
или  ?
?  или
или  ?
?
Отвечая на вопросы, ученики сравнивают соответствующие части равных полосок (для наглядности их можно закрасить разными цветами).
Рассуждения:
Сравниваю одну восьмую долю полоски и одну четвертую долю такой же полоски. Одна четвертая доля больше, чем одна восьмая доля одной и той же полоски.
Дроби величин
Задания, требующие нахождения дробей (долей) величин и величин по заданным долям используются для выработки умения находить доли от числа и число по доле не только с опорой на наглядную модель, но и с использованием смысла понятия доля.
Доля — это одна из нескольких равных частей величины.
Например:
6 листов составляют половину тетради. Сколько всего листов в тетради?
Задача может быть решена с опорой на рассуждение: половин в тетради может быть только две. Если в каждой по 6 листов, то вся тетрадь содержит 6 • 2 = 12 (листов).
Маленькая перемена длится 5 минут, что составляет четвертую часть большой перемены. Сколько минут длится большая перемена?
Рассуждение:
Четвертых частей может быть только 4. Если в каждой из них по 5 минут, то вся перемена 5 • 4 = 20 (мин).
Чему равна треть суток? Половина суток? Четверть часа? Три четверти года?
Для ответов на все вопросы используют смысл понятия доля (несколько долей) величины и знание соотношения единиц времени. Сутки — это 24 часа.
Треть суток 24: 3 = 8 (ч). Половина суток 24: 2 = 12 (ч). Час — это 60 мин. Четверть часа 60: 4 = 15 (мин). Год — это 12 месяцев. Четверть года 12: 4 = 3 (мес). Три четверти года 3-3 = 9 (мес).
Начерти отрезок, длина которого 48 мм. Чему равна длина третьей части отрезка?
Рассуждение:
Третьих частей в отрезке может быть только три. 48 мм: 3 = 16 мм — длина одной третьей части.
Начерти отрезок, пятая часть которого равна 17 мм.
Рассуждение:
Пятых частей в отрезке может быть только 5. Если каждая из них равна 17 мм, то весь отрезок 17 мм • 5 - 85 мм.
В данном контексте следует рассматривать и действия с дробями, изучаемые в начальных классах по некоторым альтернативным программам (учебник И.И. Аргинской, учебник Л.Г. Петерсон). Задания «на действия с дробями» построены на том же принципе понимания ребенком дроби как доли (или нескольких долей) предмета или множества, они не предполагают произведения действий с дробями как таковыми по принципам, определенным аксиоматикой рациональных чисел (т. е. не имеются в виду специфические преобразования знаменателей и числителей и т. п., по специальным правилам, как это делается в 5—6 классах средней школы).
Результаты действий с дробями ребенок формирует как результаты операций над объектами, данными в предметной модели или рисунке.
Например:

|

|

|

|

|

|
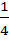 + + 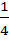 = = 
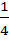 + +  = = 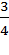
|
Рассуждения:
Одна четвертая доля полоски и еще одна такая же доля полоски — вместе две четвертых доли полоски.
Одна четвертая доля полоски и еще две таких же доли, вместе получается три четвертых доли полоски.
Следует отметить, что с точки зрения введенного определения дроби, как части объекта, числа, множества, является некорректной работа с неправильными дробями.
Неправильная дробь — это дробь, у которой числитель больше, чем знаменатель, например:
 ;
;  ;
; 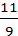 и т. п.
и т. п.
В ряде альтернативных учебников (И.И. Аргинская, Л.Г. Петерсон) практикуются задания, в которых дети должны действовать с неправильными дробями: сравнивать их, расставлять по возрастанию или убыванию и т. п.
Для того чтобы подобные задания были корректными, следует использовать другое определение дроби (как рационального числа, заданного соответственным определением; см. выше), как это сделано в учебниках средней школы.
С точки зрения используемого в начальной школе определения выражение вида  не имеет смысла, поскольку оно должно пониматься так: некий предмет (яблоко, полоску) разделили на 4 равные части, а затем взяли 7 таких частей. Речь идет об одном предмете, поэтому взять 7 частей неоткуда!
не имеет смысла, поскольку оно должно пониматься так: некий предмет (яблоко, полоску) разделили на 4 равные части, а затем взяли 7 таких частей. Речь идет об одном предмете, поэтому взять 7 частей неоткуда!
Даже если речь идет о множестве: «в классе 36 детей», то одна четвертая доля этого количества равна 9 детям, а  долей должны соответствовать количеству 64 человека — при том, что изначально их было 32!
долей должны соответствовать количеству 64 человека — при том, что изначально их было 32!
Таким образом, при желании знакомить учеников начальной школы с неправильными дробями следует по-другому построить методику их знакомства с понятием «Дроби» (сделать это на основе аксиоматического определения) и не использовать понятие «Доли» вообще.
Глава 8
|
|
|


