 |
Задания на измерение и вычисление
|
|
|
|
Задания на измерение и вычисление являются основными видами заданий, построенных на геометрическом содержании. Цель этих заданий — формирование у ребенка измерительных умений и навыков, применение имеющихся вычислительных умений к заданиям практического характера.
Рассмотрим виды заданий на измерение и вычисление по годам обучения.
1 класс
1. Сравни длину полосок с помощью одинаковых мерок.

Выполнение
Заданную мерку ребенок укладывает по длине каждого отрезка, считая их. Если отрезок содержит большее количество мерок, значит он длиннее.
2. Найди равные и неравные отрезки.

Выполнение:
Используя данную мерную полоску, ребенок прикладывает ее к каждому отрезку, отмечая количество уложившихся мерок. Равные отрезки содержат равное количество мерок.
3. Саша начертил отрезок длиной б см. Аня продолжила этот отрезок на 1 см. Какой длины получился отрезок? Начерти его.
Выполнение: Ребенок чертит по линейке отрезок длиной 6 см. Затем продолжает его на 1 см и измеряет весь получившийся отрезок (7 см).
4. Узнай длину этих отрезков в сантиметрах. Начерти в тетради отрезки такой же длины.

Выполнение:
Каждый отрезок измеряется с помощью линейки. В тетради ребенок чертит отрезки такой же длины (столько же сантиметров).
5. Чему равна длина каждой стороны треугольника и каждой стороны квадрата?

Выполнение:
Зная свойство квадрата, ребенок измеряет длину только одной стороны. Остальные стороны имеют такую же длину.
Стороны треугольника можно сначала сравнить с помощью циркуля — они равны (треугольник равносторонний), значит, можно измерить только одну сторону — остальные стороны имеют такую же длину.
6. На сколько сантиметров длина одного отрезка больше длины другого?
|
|
|
Выполнение:
Возможны два способа выполнения:
1. Длина каждого отрезка измеряется и вычисляется разница длин в сантиметрах.
2. С помощью циркуля меньший отрезок откладывается на большем, а затем разница длин измеряется.
7. Измерь длину и ширину обложки учебника в сантиметрах. Сколько это дециметров и сантиметров?
Выполнение:
Линейные размеры учебника измеряются линейкой в сантиметрах, а затем сантиметры выражаются в дециметрах и сантиметрах, например:
21 см = 2 дм 1 см
8. Начерти в тетради такую ломаную. Узнай длину каждого звена ломаной и найди сумму длин всех ее звеньев.

Выполнение:
Рисунок ломаной дан в учебнике на клетчатой поверхности. Используя подсчет клеточек, ребенок копирует рисунок в тетрадь. Затем измеряет длину каждого звена и вычисляет их сумму.
2 класс
1. Начерти отрезок длиной 10 см. Поставь на нем точку так, чтобы получился отрезок длиной 4 см. Узнай длину второго отрезка/Сравни длины полученных отрезков.
15-2681
Выполнение:
Ребенок чертит отрезок длиной 10 см. От любого края отмеряет 4 см и ставит точку — получился отрезок длиной 4 см. Измеряет длину второго отрезка — 6 см (или вычисляет ее: 10 см - 4 см = 6 см). Разницу длин находит вычислением: 6 см - 4 см = 2 см.
2. Начерти прямоугольник со сторонами 1 см и б см. Проведи в нем один отрезок, чтобы получился квадрат.
Выполнение:
Ребенок чертит прямоугольник со сторонами 1 см и 6 см.
Для получения квадрата необходимо использовать одну из сторон прямоугольника — это сторона длиной 1 см, поскольку у квадрата все стороны имеют равные длины, значит, выделить квадрат со стороной 6 см нельзя. Поэтому нужно выделять квадрат со стороной 1 см. Откладываем от любого края 1 см и проводим вертикальный отрезок, следя за тем, чтобы он пересек стороны прямоугольника под прямым углом.
3. Начерти несколько ломаных из двух звеньев так, чтобы длина каждой ломаной была равна 11 см.
|
|
|
Выполнение:
Число 11 представляется в виде суммы двух слагаемых, например: 4 + 7. Ребенок вычерчивает ломаные, имеющие соответствующие длины звеньев.
4. Начерти ломаную из четырех звеньев, длины которых 2 см, 3 см, 4 см, 2 см. Найди длину этой ломаной. Начерти отрезок, длина которого равна длине ломаной.
Выполнение:
Ломаная с соответствующими длинами звеньев вычерчивается произвольно. Найти длину ломаной можно двумя способами:
1. Вычислив сумму длин отрезков: 2 см + 3 см + 4 см + 2 см = 11 см. Затем начертить этот отрезок.
2. На прямой отложить последовательно все отрезки, получить суммарный отрезок и измерить его длину. Это и будет отрезок, длина которого равна длине ломаной.
3 класс
1. Измерь стороны треугольника ОМК(в миллиметрах) и узнай, на сколько миллиметров сумма длин отрезков ОK и ОМ больше длины отрезка КМ.
Выполнение:
Треугольник ОМК дан на рисунке в учебнике. Ребенок измеряет длины сторон в миллиметрах. Вычисляет сумму длин отрезков ОК и ОМ. Затем вычисляет разницу этой суммы и длины отрезка КМ.
2. Начерти отрезок AB длиной 60 мм. Отметь на нем точку С так, чтобы длина отрезка AС была равна 15 мм. Узнай длину отрезка СВ, не измеряя его.
Выполнение:
Ребенок чертит отрезок АВ по линейке. Отмеряет от точки А 15 мм, получает отрезок АС. Длину отрезка СВ находит вычислением: 60 мм - 15 мм = 45 мм
3. Вычисли периметры многоугольников в сантиметрах.

Выполнение:
Длины сторон фигур ребенок измеряет линейкой и вычисляет периметр (сумму длин сторон). У четырехугольника противолежащие стороны равны, поэтому можно, выяснив это с помощью циркуля, вычислять его периметр рациональным способом: найти сумму двух рядом лежащих сторон, а затем умножить это число на 2. У пятиугольника все стороны равной длины. Выяснив это с помощью циркуля, можно измерить одну сторону, а затем умножить ее длину на 5.
4. Чему равна сторона квадрата, если его периметр равен периметру прямоугольника со сторонами 5 см и 3 см?
Выполнение:
Вычисляется периметр прямоугольника: (5 см + 3 см) • 2 = 16 см. Этот периметр равен периметру квадрата. Поскольку у квадрата все стороны равны, значит, сторона квадрата равна: 16 см: 4 см = 4 см.
5. Начерти два отрезка так, чтобы длина одного была 4 см, а длина другого — в 2 раза больше. Обозначь отрезки буквами и узнай, на сколько сантиметров один из них меньше другого.
|
|
|
Выполнение:
Вычерчивается отрезок длиной 4 см. Длина другого 4 см • 2 = 8 см. Разницу длин находят вычислением 8 см - 4 см = 4 см.
6. Вычисли площадь прямоугольника, длины сторон которого 9 см и 2 см.
Выполнение:
Площадь прямоугольника находится как произведение длин сторон. Значит 9 см • 2 см = 18 см2.
7. Найди длину стороны квадрата ABCD, периметр которого 8 см. Начерти его и вычисли площадь.
Выполнение:
Периметр квадрата — это сумма длин всех его сторон, значит одна сторона квадрата 8 см: 4 = 2 см (поскольку стороны квадрата имеют равные длины). Площадь квадрата — это произведение длин его сторон: 2 см • 2 см = 4 см2.
8. Измерь радиус данной окружности и начерти окружность такого же радиуса.

Выполнение:
Проводим радиус окружности, соединяя центр с любой точкой окружности. Измеряем ее циркулем и вычерчиваем окружность такого же радиуса.
9. Начерти три отрезка: длина первого отрезка 8 см, длина второго составляет одну четвертую длины первого, а длина третьего на 6 см больше длины второго.
Выполнение:
Первый отрезок вычерчивается по заданной длине. Длина второго сначала вычисляется: 8 см: 4 = 2 см. Длина третьего отрезка также сначала вычисляется: 2 см + 6 см = 8 см.
10. Начерти квадрат, площадь которого равна площади прямоугольника со сторонами 2 см и 8 см. Найди периметр этого квадрата.
Выполнение:
1. Вычислим площадь прямоугольника: 2 см • 8 см = 16 см2.
2. Эта площадь равна площади квадрата. Площадь квадрата равна произведению длин его сторон, значит, нужно подобрать число, произведение которого на само себя равно 16 — это число 4. Длина стороны квадрата 4 см. Периметр квадрата 4 см • 4 = 16 см.
11. Периметр равностороннего треугольника 24 см. Чему равна длина каждой его стороны?
Выполнение:
Равносторонний треугольник имеет стороны равной длины, значит 24 см: 3 = 8 см — длина стороны треугольника.
12. Из трех одинаковых квадратов составили прямоугольник. Узнай периметр этого прямоугольника, если сторона каждого квадрата равна 16 мм.
|
|
|
Узнай сторону квадрата, периметр которого равен периметру этого прямоугольника.
Выполнение:
Для решения этой задачи удобно выполнить рабочий рисунок (примерный):
| 16 мм |
| 16 мм |
| 16 мм |
| 16 мм |
| 16 мм |
| 16 мм |
| 16 мм |
| 16 мм |
Анализ рисунка показывает, что для нахождения периметра прямоугольника нужно 16 мм • 8 = 128 мм.
Если считать это число периметром квадрата, можно определить длину его стороны: 128 мм: 4 = 32 мм.
4 класс
1. Начерти луч с началом в точке К. Отложи на нем от его начала один за другим несколько отрезков длиной по 15 мм. Отметь на луче точки А, В, С, соответствующие числам 4, 6, 8. Найди длины отрезков КА, KB, АС, ВС.
Выполнение:
Выполнять задание следует по чертежу:
| K |
| A |
| B |
| C |
По рисунку определяем длины отрезков:
КА — 4 единицы по 15 мм, КА = 15 мм • 4 = 60 мм.
KB — 6 единиц по 15 мм, KB = 15 мм • 6 = 90 мм.
АС — 4 единицы по 15 мм, АС = 15 мм • 4 = 60 мм.
ВС — 2 единицы по 15 мм, ВС = 15 мм • 2 = 30 мм.
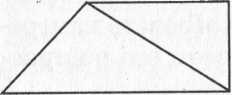
2. Рассмотри чертеж и объясни, как найти площадь треугольника ACD.
| K |
| D |
| M |
| A |
| B |
| C |
Выполнение:
Треугольник ACD состоит из двух треугольников: ADK и АСК
Треугольник ADK составляет половину квадрата DMAK, значит, его площадь равна половине этого квадрата.
Треугольник АСК составляет половину прямоугольника АВСК, значит, его площадь равна половине площади этого прямоугольника.
Можно заметить, что квадрат DMAK и прямоугольник АВСК составляют вместе прямоугольник DMBC, значит, площадь искомого треугольника Л CD составляет половину площади прямоугольника DMBC
Измеряем длины сторон прямоугольника DMBC, находим его площадь как произведение длин сторон, и делим полученное число пополам.
3. Начерти два отрезка. Длина первого 8 см. Это в 2 раза больше длины второго отрезка. На сколько сантиметров длина первого отрезка больше длины второго?
Выполнение:
Вычерчиваем первый отрезок длиной 8 см. Затем задание требует переформулировки: если это (8 см) в два раза больше, чем второй отрезок, значит, второй отрезок в два раза меньше, чем первый. Следовательно, длина второго отрезка 8 см: 2 = 4 см.
4. Вырежи квадрат со стороной 8 см. Раздели его перегибанием на 4 равных треугольника и найди площадь каждого из них.
Выполнение:
Для нахождения площади искомого треугольника нужно сначала найти площадь квадрата 8 см • 8 см = 64 см2, а затем разделить ее на 4, поскольку все треугольники равные 64 см2:4 = 16 см2.
5. Длина прямоугольника 8 см, его периметр 24 см. Начерти такой прямоугольник, раздели его на два равных треугольника. Какие получились треугольники: остроугольные, тупоугольные или прямоугольные? Найди площадь каждого треугольника.
|
|
|
Выполнение:
Для того чтобы начертить такой прямоугольник, нужно знать длину его второй стороны.
| 8 см |
| ? |
| 8 см |
Сумма длин двух сторон 8 см + 8 см = 16 см, значит сумма двух других сторон 24 см - 16 см = 8 см. Стороны равной длины, значит, 8 см: 2 = 4 см — длина другой стороны (ширина). Теперь прямоугольник можно построить.
Разделив его на два равных треугольника диагональю, получаем прямоугольные треугольники. Чтобы найти площадь одного из них, разделим площадь прямоугольника пополам:
8-4 = 32 см2; 32 см2: 2 = 16 см2
6. Найди диаметр большего круга, если радиус меньшего равен 1 см.

Выполнение:
Если радиус меньшего круга равен 1 см, то его диаметр будет равен 2 см, поскольку диаметр круга равен двум радиусам.
Анализ рисунка показывает, что диаметр меньшего круга равен радиусу большего круга. Значит, радиус большего круга равен 2 см, тогда его диаметр равен 4 см.
7. Начерти любую окружность. Проведи в ней два любых диаметра, соедини их концы отрезками и найди площадь полученного прямоугольника.
Выполнение:
Полученный таким образом четырехугольник будет прямоугольником. Это необходимо проверить, измерив его углы угольником. Затем измеряются длины двух рядом лежащих сторон и находится площадь по формуле: площадь прямоугольника равна произведению длин его сторон.
Задания на построение
Задания на построение составляют важную часть системы формирования геометрических знаний и умений ребенка в начальной школе. Эти задания создают базу для развития пространственного воображения у ребенка, умения наблюдать, сравнивать, обобщать, анализировать и абстрагировать. Необходимость формирования у ребенка практических умений построения геометрических фигур с помощью циркуля, угольника и линейки и подготовки к обучению рассуждениям и доказательству является важнейшей задачей курса начальной математики с точки зрения дальнейшего математического образования ребенка. Как доказано психологами, возраст ученика начальной школы является наиболее благоприятным в жизни человека возрастом для развития образного (а значит, и пространственного) мышления, формирования приемов умственных действий (сравнения, обобщения, абстрагирования и др.). Анализ особенностей этапов развития математического мышления ребенка показывает также необходимость организации подготовки к обучению доказательствам в период обучения в начальной школе.
Рассмотрим виды заданий на построение по годам обучения и покажем возможности их использования для развития указанных компонентов мышления.
1 класс
1. Начерти в тетради ломаную, состоящую из четырех звеньев. Сколько вершин у этой ломаной?
Выполнение:
По определению, концы каждого звена — это вершины ломаной. Таким образом, ломаная из 4 звеньев будет иметь 5 вершин, если она незамкнутая, и 4 вершины, если она замкнутая:

2. Вырежи из приложения нужные фигуры и составь из них домик, кораблик, рыбку (по рисунку, данному в учебнике).
Выполнение:

Задания такого вида представляют собой конструктивные задачи на развитие операции синтеза (конструирование целого из частей). В учебнике эти задания встречаются вплоть до 4 класса, но особенно важны они в 1 классе. Если у ребенка возникают затруднения, следует сделать для него увеличенный вариант рисунка, чтобы можно было складывать заданную фигуру, накладывая ее части прямо на рисунок.
Эти задания являются подготовительными для заданий вида: сколько на чертеже треугольников, четырехугольников и т. п.
В их основе лежит операция анализа (умение мысленно «разобрать» объект на составные части и выделить каждую из них). Практика показывает, что при хорошей подготовке посредством выполнения заданий на конструирование (синтез), задания данного вида даются ребенку намного легче.
3. Начерти один четырехугольник. Проведи 1 отрезок, чтобы получилось 2 треугольника.
Выполнение:
При выполнении данного задания полезно рассмотреть разные варианты его выполнения - это развивает гибкость мышления и пространственное воображение. Полезно сравнить полученные результаты, сделав обобщение: для того чтобы получилось 2 треугольника, нужно проводить в четырехугольнике диагональ.

4. Как можно провести в треугольнике 1 отрезок так, чтобы получилось 3 треугольника?
Выполнение:

Достаточно провести 1 отрезок так, чтобы разделить данный треугольник на 2 треугольника. В качестве третьего рассматриваем исходный треугольник (содержащий два меньших).
5. Составь из 7 палочек 2 одинаковых квадрата, а из 10 палочек 1 большой квадрат и 1 маленький.
Выполнение:
Задание на конструирование из палочек (см. характеристику задания 2).
6. Начерти одну ломаную, у которой 4 звена и 5 вершин, а другую — у которой 4 звена и 4 вершины.
Выполнение:
См. характеристику задания 1.
7. Начерти любой четырехугольник и проведи в нем 2 отрезка так, чтобы получилось 8 треугольников.
Выполнение:
При выполнении данного задания полезно рассмотреть разные варианты его выполнения — это развивает гибкость мышления и пространственное воображение. Полезно сравнить полученные результаты, сделав обобщение: для того, чтобы получилось 8 треугольников, нужно проводить в четырехугольнике две диагонали.

Каждый четырехугольник содержит 4 маленьких треугольника, а также 4 треугольника, составленных из двух расположенных рядом маленьких треугольников.
2 класс
1. Проведи прямую, отметь на ней 3 точки. Сколько всего отрезков получилось?
Выполнение:
Задание аналитического характера: всего отрезков три: два меньших, обозначенных точками, и в качестве третьего рассматриваем отрезок, содержащий оба меньших отрезка (фактически: два отрезка являются частями третьего).
2. Начерти и дополни до прямоугольника:

Выполнение:
Задание развивает воссоздающее воображение, требует воссоздания целого по его частям. Поскольку в учебнике эти задания даны на клетчатой основе, их выполнение не требует применения инструментов при достроении, достаточно производить ориентировку на количество клеточек, восстанавливая форму заданной фигуры.
3. Как провести в каждом из этих четырехугольников 1 отрезок, чтобы получился квадрат?

Выполнение:
Задание обратное по типу заданию 2. Требует анализа и выделения части из целого. Оно также дано в учебнике на клетчатой основе, поэтому не требует применения инструментов. Для его выполнения достаточно ориентировки по клеточкам и соблюдения равенства сторон квадрата.
4. Сложи из треугольников нарисованные фигуры (по рисунку в учебнике).
Выполнение:
См. выше характеристику задания 2 из 1 класса.
3 класс
1. Начерти два отрезка так, чтобы длина одного была в два раза больше длины данного отрезка, а длина другого — в 2 раза меньше длины данного.
Выполнение:
Чтобы начертить отрезок в 2 раза больше данного, можно измерить его циркулем, и отложить на прямой последовательно два таких отрезка:
Полученный таким образом отрезок будет в два раза больше данного.
Чтобы начертить отрезок в два раза меньше данного, нужно разделить данный отрезок пополам, и построить отрезок, равный половине данного. Поскольку техника деления отрезка пополам с помощью циркуля предлагается детям для знакомства только на последней странице учебника 4 класса, очевидно, предполагается, что для выполнения этого задания следует использовать измерение и вычисление длины искомого отрезка, а потом его построение по известной длине.
Можно познакомить ребенка с техникой деления отрезка пополам с помощью циркуля:
2. Начерти на клетчатой бумаге и вырежи прямоугольник и два треугольника, как на чертеже.
Составь из этих фигур: четырехугольник, пятиугольник. Сравни площади составленных фигур.

Выполнение:
Задание конструктивного характера. Цель задания — показать ребенку, что равносоставленные фигуры имеют равные площади. Полезно составить различные по форме четырехугольники и убедиться в том, что пятиугольник получается только одной формы:
3. Начерти три таких четырехугольника. В каждом из них проведи один отрезок так, чтобы он разделил четырехугольник:
1) на два треугольника;
2) на треугольник и прямоугольник;
3) на квадрат и четырехугольник.
Выполнение:
См. характеристику задания 3 из 2 класса.
4. Начерти в тетради пятиугольник и покажи на чертеже, как можно двумя взмахами ножниц разрезать этот пятиугольник так, чтобы получилось 2 четырехугольника и 1 треугольник.
Выполнение:
Полезно рассмотреть разные варианты выполнения задания:

5. Начерти в тетради любую фигуру, кроме прямоугольника, так, чтобы ее площадь была 12 см2.
Выполнение:
По условию фигура не может быть прямоугольником (а значит, и квадратом). Площади фигур другой формы ученики 3 класса умеют находить только способом подсчета квадратных сантиметров. Значит, следует рисовать фигуру произвольной формы, составленную из квадратиков по 1 см2.
Другой, более сложный вариант: начертить прямоугольник площадью 24 см2. Разделить его пополам — получится треугольник площадью 12 см2.
4 класс
1. Начерти в тетради прямой, острый и тупой углы с общей вершиной в точке В разными цветными карандашами.
Выполнение:
Полезно обратить внимание ребенка на то, что получается 2 тупых угла:

| B |
2. Начерти в тетради четырехугольник ABCD, как на рисунке. Проведи в нем отрезок ВМ так, чтобы угол ВМС был прямым.

а а
Выполнение:
Для выполнения задания фактически требуется умение опускать перпендикуляр из точки на прямую, однако здесь предполагается, что ребенок, используя угольник, ищет позицию совмещения его сторон с отрезком CD и точкой В.
3. Начерти отрезки, как показано на чертеже. Соедини точки так, чтобы получился четы-_ рехугольник. Проверь, квадрат ли это.
Выполнение:
Рисунок в учебнике дан на клетчатой основе, поэтому его копирование требует только подсчета клеток. Получившаяся фигура будет квадратом. Задание иллюстрирует свойство диагоналей квадрата: диагонали квадрата при пересечении образуют прямой угол и делятся в точке пересечения пополам.
4. Рассмотри чертеж и начерти в тетради квадрат, диагональ которого равна 4 см. Проведи окружность так, чтобы она прошла через все вершины квадрата.

Выполнение:
Задание, аналогичное заданию 3 с добавлением заданной длины диагонали. Выполняется на основе подсчета клеток и свойств диагоналей квадрата. Точка пересечения диагоналей квадрата является центром описанной (и вписанной) окружности.
5. Начерти окружность, проведи в ней диаметр и соедини концы диаметра с любой точкой окружности. Какого вида треугольник получился?

Выполнение: Получится прямоугольный треугольник. Задание иллюстрирует свойство вписанного угла, опирающегося на диаметр.
6. Начерти прямой угол с вершиной в точке О. Отложи от точки О на сторонах угла равные отрезки OA и ОВ длиной по 3 см. Соедини отрезком точки А и В. Какого вида треугольник получился? Дай два ответа.
Выполнение:
Получится равнобедренный треугольник, который также является прямоугольным.
7. Начерти разносторонний прямоугольный треугольник; равнобедренный тупоугольный треугольник.
Выполнение:
Задание проверяет умение ребенка соблюдать два заданных признака при выполнении чертежа:

Следует обратить внимание на то, что построение равнобедренного тупоугольного треугольника требует также знания способа построения равнобедренных треугольников.
8. Начерти любой прямоугольник, проведи в нем диагонали. Построй окружность с центром в точке их пересечения, которая проходит через все его вершины. (На полях дан полный чертеж.)
Выполнение:
Поскольку в учебнике дан на полях полный чертеж задания, оно требует лишь копирования образца.
Задание иллюстрирует следующее свойство прямоугольника: точка пересечения диагоналей прямоугольника является центром описанной окружности.
9. Начерти в тетради прямоугольник ABCD со сторонами 3 см и 4 см. Проведи в нем 2 отрезка так, чтобы получилось 8 треугольников.
Выполнение: См. характеристику задания 7 из 1 класса.
10. Построить равносторонний треугольник.
Выполнение:
В учебнике приведен полный чертеж, требуется лишь копирование образца.
11. Построить равнобедренный треугольник.
Выполнение:
См. характеристику задания 10.
12. Построить треугольник по трем заданным сторонам.
Выполнение:
См. характеристику задания 10.
13. Раздели отрезок пополам с помощью циркуля.
Выполнение:
См. характеристику задания 10.
Сравнение количества и качества заданий на построение и заданий на измерение и вычисление показывает, что заданиям на измерение и вычисление уделено в учебниках намного больше внимания. С качественной (а также перспективной) точки зрения, в дальнейшем ребенку будут необходимы в большей мере умения по построению и доказательству правильности построения, поскольку они лежат в основе умения решать задачи и доказывать теоремы в курсе геометрии и выполнять чертежи в курсе черчения.
Глава 6
|
|
|


