 |
P(t)=exp(−λt) = exp (-3*10-4*100) = 0,998.
|
|
|
|
P(t)=exp(− λ t) = exp (-3*10-4*100) = 0, 998.
Математическое ожидание наработки на отказ равно Мх = 1/ λ = 1 / 3*10-4 = 3, 33*103.
4. 3. Нормальный закон распределения
Нормальный закон распределения часто называют законом Гаусса. Этот закон играет важную роль и наиболее часто используется на практике по сравнению с другими законами распределения.
Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надёжности его используют для описания постепенных отказов, когда распределение времени безотказной работы вначале имеет низкую плотность, затем максимальную и далее плотность снижается.
Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы.
Нормальный закон распределения описывается следующей зависимостью:
f (x) =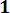 
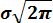
exp {– (x-m) / 2σ 2}, (3. 7)
где е = 2, 71828 – основание натурального логарифма; π = 3, 14159;
т и σ –параметры распределения, определяемые по результатам
испытаний; Х – случайная величина.
Кривая плотности распределения приведена на рис. 3. 2.
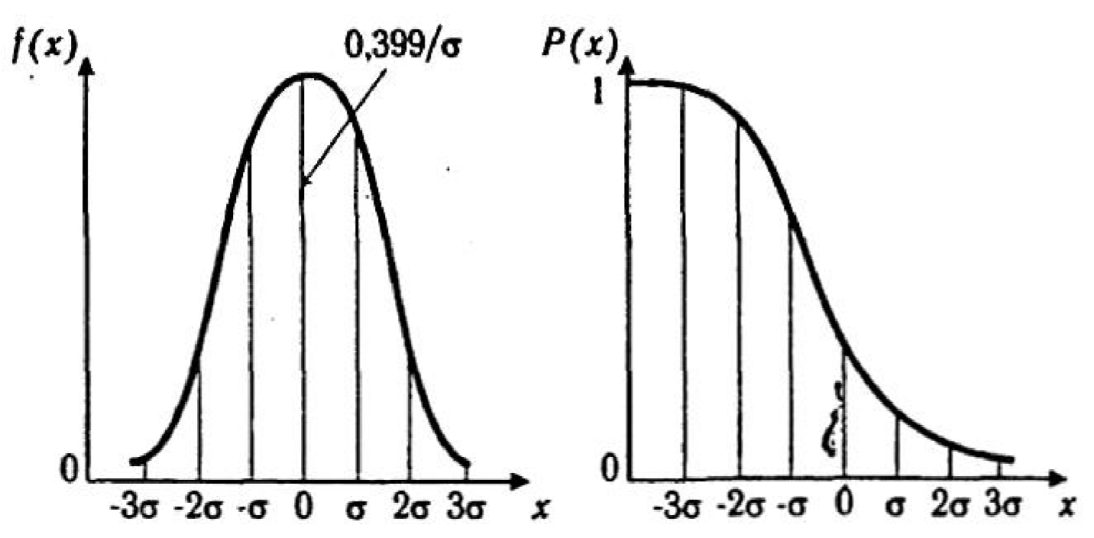
а б
Рис. 3. 2. Кривые плотности вероятности (а) и функции надежности
(б) нормального распределения
Параметр т = Мx представляет собой среднее значение случайной величины X, оцениваемое по формуле
Мх =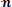 
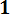
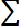
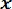
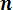
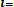
. (3. 8)
параметр σ – среднее квадратическое отклонение случайной величины X, оцениваемое по формуле
____________________
|
|
|
s = √ {1/( n-1) -
Mx). (3. 9)
Интегральная функция распределения имеет вид
x
F (x) =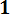 
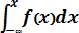
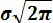
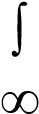exp {– (x-m)2 / 2σ 2} dx, (3. 10)
-
вероятность отказа и вероятность безотказной работы соответственно Q (x) =F(x), Р(х) =1 -F(x).
Вычисление интегралов заменяют использованием таблиц нормального распределения, при котором Мx = 0 и σ = 1. Для этого распределения функция плотности вероятности имеет одну переменную t и выражается зависимостью.
f0 (t) =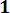 
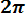exp(-t2/2), (3. 11)
Величина t является центрированной (так как Мt = 0 ) и нормированной (так как σ t = 1 ).
Функция распределения (функция Лапласа) соответственно запишется в виде:
t
F
| ( |
| = |
| t) |
| ∫ |
-∞
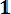
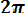
Из этого уравнения следует, что F0 (t )+ F0 (-t) = 1 или F (t)= 1 - F0 ( t ).
При использовании табл. 1 приложения [4] следует в формулу (3. 13) вместо t подставить
ее значение: t = (t – Mx)/ σ , (3. 13)
при этом t называют квантилью нормированного нормального распределения (обычно обозначают up).
Плотность распределения и вероятность отказа соответственно равны : f(x) = f0(t)/σ; Q (x)= F0 ( t );
тогда вероятность безотказной работы
Р(х) = l - F0(t), где f0(t) и F0(t), определяют по таблицам.
В табл. 1 П1 приложения [4] приведены значения Ф*(t) в зависимости от t = x = (t – Mx)/σ.
В работах по надежности часто вместо интегральной функции распределения F0(t) используют функцию Лапласа:
t
Ф
| *( |
| х |
| ) |
| = |
| ∫ |
-∞
|
|
|
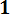
При этом,
F0(t) =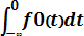 
| + |
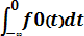= 0. 5 + Ф*(t)
(3. 15) Вероятности отказа и безотказной работы, выраженные через функцию Лапласса:
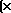
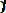
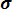
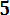
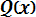
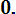
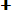
Ф*( , Р(х) = 0, 5 - Ф*(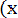 
,
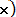
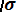
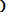
(3. 16)
Вероятность попадания случайной величины Х в заданный интервал значений от α до β вычисляют по формуле
P (α < x < β ) = Ф*( - Ф*( .
(3. 17)
Пример 3. 3. Определить вероятность безотказной работы P(t) в течение t = 2*104 ч подшипника скольжения, если ресурс по износу подчиняется нормальному закону распределения с параметрами
Mt = 4*104 ч, σ = 104 ч.
Р е ш е н и е. Находим квантиль
up= = (2*104 – 4*104)/104 = - 2.
По табл. П. 1приложения [4] определяем, что Р(t) =0, 0228.
Пример 4. 4. Пусть случайная величина Х представляет собой предел текучести стали. Опытные данные показывают, что предел текучести имеет нормальное распределение с параметрами M = 650 МПа, σ = 30 МПа. Найти вероятность того, что полученная плавка стали имеет предел текучести в интервале 600 — 670 МПа.
Р е ш е н и е. Для определения вероятности воспользуемся формулой (3. 17)
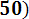
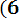
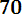
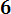
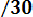
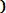
P ( 600< Х < 670) = Ф*( 
- Ф*(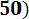 
=
|
|
|
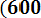
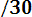
