 |
Рисунок 20. Случаи, когда необходима мнимая операция
|
|
|
|
Рисунок 20. Случаи, когда необходима мнимая операция
Критический путь
На сетевом графике с параллельными работами, от начала до конца проекта идут несколько последовательностей работ. Эти последовательности называются путями. Самый длинный путь называется критическим путем сети. (Отметьте себе, что у сети может быть несколько критических путей, если они занимают одинаковое время). Путь называется критическим, потому что любая задержка на нем приводит к задержке всего проекта. Таким образом, на рисунке 19 критическим является путь а, b, c, f, длительностью 7 дней. Это минимальная продолжительность всего проекта.
Рисуя сетевой график, мы можем:
· Выявить самые важные работы;
· Рассчитать продолжительность проекта.
Расчет резерва времени
Ранее мы уже говорили о том, что возможность гибко изменять сроки начала работ объясняется наличием резерва времени. Теперь мы используем сетевой график для вычисления резерва времени по каждой работе. Сделать это не трудно.
1. По каждому событию вычисляется раннее и позднее время события (РВС и ПВС). Раннее время наступления события - самое раннее из возможных время наступления события, при условии завершения всех предыдущих работ в кратчайшие сроки. Позднее время наступления события - самое позднее из возможных время наступления события без задержки всего проекта.
2. Вычисляется “временное окно” в пределах которого должна быть выполнена работа. Это разница между РВС ее хвостового события и ПВС ее головного события.
3. Фактическая продолжительность работы сравнивается с временным окном, в пределах которого она должна быть выполнена. Разница между этими показателями является резервом времени работы.
|
|
|
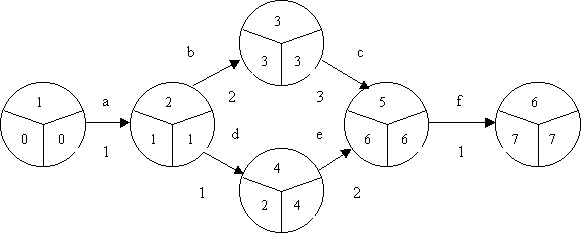
Рассмотрим простой пример сетевого графика. Критический путь - это последовательность работ (a), (b), (c), (f). Мы можем вычислить РВС и ПВС для каждого события, как показано на рисунке 21.
Рисунок 21. Сетевая диаграмма для проекта ремонты квартиры с самыми ранними и самыми поздними временами наступления событий
Если работа (а) начинается в момент времени 0, то самое раннее время ее окончания - 1, поскольку эта работа выполняется в течение дня. Если работа (b) начинается сразу после работы (а), она закончится в день 3 (РВС хвостового события + продолжительность = 1 + 2). В день 3 начинается работа (с), и поскольку она имеет трехдневную продолжительность, то завершится в день 6. Головным событием работы (е) является событие 5, так что мы должны также рассчитать РВС хвостового события работы. Оно определяется работой (d). Если работа (d) начинается в день 1 (раннее начало), она завершится в день 2. Поэтому РВС события 4 - день 2. Если работа (е) начнется немедленно, то она завершится в день 4. Событие номер 5 не может состояться до завершение событий (е) и (с), то есть, до дня 6 (смотри правило 1 выше). После этого начнется работа (f), которая завершится в день 7.
ПВС можно рассчитать, используя обратную логику. Если событие номер 6 должно произойти не позднее дня 7, то ПВС для события номер 5 есть день 6. Любое опоздание после этого срока означает задержку всего проекта. Далее по пути назад, если работа (с) должна закончиться ко дню 6, она не может начаться позднее дня 3, если работа (b) должна завершиться ко дню 3, то она должна начаться в день 1. Таким же образом, если работа (е) должна завершиться в день 6, то она должна начаться не позднее дня 4, и если работа (d) должна завершиться ко дню 4, то она должна начаться не позднее дня 3. Теперь у нас имеются две работы, которые имеют событие 2 в качестве своего хвостового события, причем одна из них должна начаться самое позднее в день 1, другая - самое позднее в день 3. Поэтому ПВС для события номер 2 должно иметь меньшее значение из двух. Если оно состоится позже этого, то будет задержана работа (b), а значит и весь проект.
|
|
|
Операции в узлах сети
Для представления работ описанная нами сеть использует стрелки (дуги) и кружки (узлы, вершины) на пересечении стрелок для представления событий. Этот метод называется операции на дугах (ОД). Другой метод представления сетей называется методом операций в узлах (ОУ). В соответствии с этим методом, работы изображаются прямоугольниками, а стрелки показывают зависимости между ними. Этот метод обладает тремя преимуществами:
· Построить сетевой график на основе базовой логики проекта легче с использованием метода ОУ нежели ОД.
· Графики ОУ не нуждаются в мнимых работах для поддержания логики зависимостей.
· Большинство программных пакетов управления проектами используют формат ОУ.
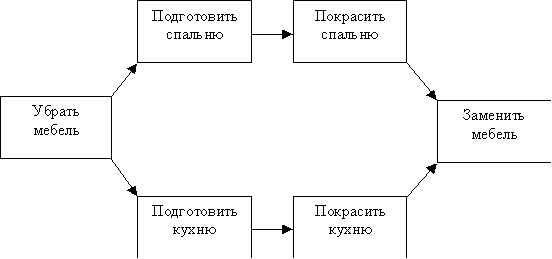
Пример сетевого графика для проекта ремонта квартиры представлен на рисунке 22.
Пример
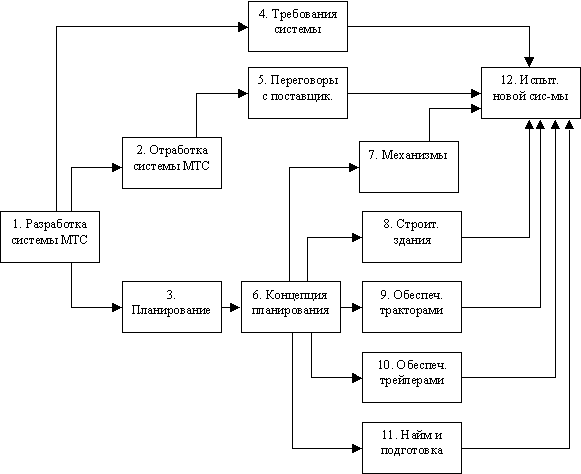
Ниже на рисунке 23 представлен сетевой график операций в узлах проекта материально технического снабжения, о котором говорилось выше. В этом примере, как и в реальных примерах, зависимости не всегда явны. Например, операция “уточнение решения” показана как влияющая только на “переговоры с поставщиком. На деле же, эта операция влияет также на “системные требования”, вероятно также на операции с 7 по 11. Такие зависимости могут быть показаны на сетевом графике нижнего уровня, то есть на более подробном графике. Сама по себе работа “системные требования” уже является самостоятельным проектом, требующим для планирования и управления собственных линейных и логических диаграмм.
|
|
|


