 |
Практическое занятие 1 «использование финансовых функций для расчета эффективности инновационных проектов»
|
|
|
|
Е. П. ЯХИНА
ИННОВАЦИИ В СФЕРЕ СЕРВИСА
Методические указания к выполнению практических работ
На правах рукописи
Омск
Я 90
Ответственный за выпуск:
канд. пед. наук, заведующий кафедрой ПрИМ ОГИС О. Н. Лучко
Яхина, Е. П.
Я 90 Инновации в сфере сервиса: учебное пособие / Е. П. Яхина. – Омск: Омский государственный институт сервиса, 2010. – 42 с.
ISBN
Целью настоящего учебного пособия является обеспечение студентов информацией, необходимой для практического освоения курса «Инновации в сфере сервиса».
Пособие рассчитано для студентов дневного и заочного отделения специальности «Прикладная информатика» качестве основного и дополнительного материала при подготовке к лекциям и практическим занятиям по данному курсу.
| ISBN | © Омский государственный институт сервиса |
ОГЛАВЛЕНИЕ
Предисловие. 4
Практическое занятие 1 «использование финансовых функций для расчета эффективности инновационных проектов». 5
Функция БС.. 8
Функция ПС.. 8
Функция КПЕР.. 9
Функция СТАВКА.. 10
Функция ПЛТ. 10
Функция ЧПС.. 12
Задачи для самостоятельной работы.. 13
Практическое занятие 2 «Расчет финансовых показателей для оценки инновационных проектов». 15
Пример. 16
Задачи для самостоятельной работы.. 17
Практическое занятие 2 «Оптимизационные модели». 18
Задача составления скользящих графиков. 20
Задача оптимизации инвестиций.. 22
Задача логического выбора. 23
Задачи для самостоятельной работы.. 25
Практическое занятие 3 «Принятие решений на основе прогнозирования» 28
Причинно-следственные модели.. 29
Модели временных рядов. 29
Задачи для самостоятельной работы.. 31
|
|
|
Практическое занятие 4 «финансовый анализ в project expert» 33
Библиографический список. 42
Предисловие
Предисловие
Цель управления инновациями состоит в том, чтобы инициировать, генерировать, контролировать новые идеи и управлять ими в масштабах всей организации и выводить полученные результаты на рынок. В основе управления инновациями лежит сбалансированное сотрудничество новаторов и тех, кто отвечает за направление деятельности организации и ее стабильность. Для надлежащего управления творческими процессами необходимо найти и устранить помехи на пути инноваций, обеспечить мотивацию и создать такие отношения в организации, которые будут поддерживать личную и групповую инновационную инициативу.
В современных условиях инновационная деятельность является важнейшей составляющей процесса обеспечения успешного функционирования предприятия. В связи с этим возникает необходимость проведения экономического анализа этой деятельности.
Настоящий курс раскрывает основные понятия и методы инновационной деятельности и призван помочь студентам использовать их в конкретной практической деятельности.
Пособие рассчитано на студентов вузов, получающих образование по разным формам обучения.
Е. П. Яхина
Практическое занятие 1 «использование финансовых функций для расчета эффективности инновационных проектов»
Цель: научить студентов использовать аппарат Excel для оценки инновационных проектов.
Используемое программное обеспечение: операционная система Windows, Ms Excel.
Время выполнения работы: 4 часа аудиторных занятий.
Особенностью всех финансовых расчетов является временная ценность денег, т. е. принцип неравноценности денег, относящихся к разным моментам времени. Предполагается, что полученная сегодня сумма обладает большей ценностью, чем ее эквивалент, полученный в будущем, т. е. будущие поступления менее ценны, чем современные.
|
|
|
Неравноценность одинаковых по абсолютной величине сумм связана, прежде всего, с тем, что имеющиеся сегодня деньги могут быть инвестированы и принести доход в будущем. Основными понятиями финансовых методов расчета являются:
· процент – абсолютная величина дохода от предоставления денег в долг в любой ее форме;
· процентная ставка –величина дохода за фиксированный интервал времени, измеряемая в процентах или в виде дроби;
· период начисления – интервал времени, к которому приурочена процентная ставка;
· капитализация процентов – присоединение начисленных процентов к основной сумме;
· наращение – увеличение первоначальной суммы в связи с капитализацией;
· дисконтирование – приведение стоимостной величины, относящейся к будущему, на некоторый, обычно более ранний, период времени (операция обратная наращению);
· реальная стоимость денег – то количество потребительских благ, которое можно приобрести в обмен на определенную денежную сумму.
Очень часто на практике встречается понятие потока платежей. Заработная плата, плата за квартиру — потоки ежемесячных платежей и т. д. Поэтому изучение потоков платежей очень важно.
Поток платежей — это последовательность величин самих платежей (со знаками) и моментов времени, когда они осуществлены. Платеж со знаком плюс, который может быть опущен, — это поступление, платежи со знаком минус представляют собой выплаты.
Поток положительных платежей с постоянными промежутками между ними называется рентой. Часто сами платежи также являются одинаковыми.
Существуют различные способы начисления процентов от предоставления денег в долг в любой форме. За основу берется база начисления процентов. Применяются постоянная и последовательно изменяющаяся база для расчета. В последнем случае за базу принимается сумма, полученная на предыдущем этапе наращения.
При постоянной баз е начисляются простые проценты, при переменной – сложные. В случае начисления простых процентов начисление происходит по схеме:
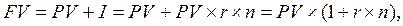
(14)
где PV – первоначальная денежная сумма;
FV – сумма денег после начисления процентов;
I – процентные деньги;
|
|
|
n – число периодов начисления процентов;
r – годовая процентная ставка.
В финансовой практике основная часть расчетов ведется с использованием схемы сложных процентов. Применение схемы сложных процентов целесообразно, если проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга или выдается ссуда сроком более одного года. Формула сложных процентов имеет вид:
 (15)
(15)
где FV – наращенная сумма;
PV – первоначальная сумма;
r – процентная ставка за период начисления;
n – число периодов начисления.
Ms Excel содержит встроенную категорию функций, которые позволяют вычислять характеристики финансовых операций, связанные с наращением и дисконтированием сумм. В таблице 23 приведены некоторые из функций и их характеристики.
Таблица 23
Функции Excel для оценки операций по вкладам и займам
| Наименование функции | Формат функции | Назначение функции |
| БС | БС (Ставка; Кпер; Плт; Пс; [тип]) | Рассчитывает будущую стоимость периодических постоянных платежей и будущее значение вклада (или займа) на основе постоянной процентной ставки |
| ПС | ПС (Ставка; Кпер; Плт; Бс; [тип]) | Рассчитывает текущую стоимость как единой суммы вклада (займа), так и будущих фиксированных периодических платежей. Является обратной к функции БС. |
| КПЕР | КПЕР (Ставка; Плт; Пс; Бс; [тип]) | Вычисляет количество периодов начисления процентов. |
| СТАВКА | СТАВКА (Кпер; Плт; Пс; Бс; [тип]) | Вычисляет процентную ставку за период начисления. |
| ПЛТ | ПЛТ (Ставка; Кпер; Пс; Бс; [тип]) | Рассчитывает сумму постоянных периодических платежей. |
Как видно из приведенной таблицы, большинство финансовых функций имеет набор базовых аргументов:
1. Ставка – процентная ставка за период (норма доходности или цена заемных средств). Например, если получена ссуда под 10 % годовых и делаются ежемесячные выплаты, то ставка за месяц составит 10 %/12 или 0,83 %.
2. Кпер – срок (число периодов) проведения операции. Например, при ссуде на 4 года с ежемесячными платежами кпер равно 4*12 (или 48) периодов.
|
|
|
3. Плт – выплата, производимая в каждый период и не меняющаяся за все время выплаты ренты.
4. Пс – приведенная к текущему моменту стоимость (PV).
5. Бс – требуемое значение будущей стоимости.
6. [ тип ] – число 0 или 1, обозначающее, когда должна производиться выплата (1 – в начале периода (обычная рента или пренумерандо), 0 – в конце периода (постнумерандо).
Рассмотрим примеры использования функций.
Функция БС
Рассчитать какая сумма окажется на счете, если 27 рублей положены на 33 года под 13,5 % годовых. Проценты раз в полгода.
Решение
Обратим внимание, что в задаче указаны годовой процент и число лет. Если проценты начисляются несколько раз в год, то необходимо рассчитать число периодов накопления процентов и ставку процента за период начисления. На рисунке 28 показано решение задачи.
 |
Рис. 28. Решение задачи с использованием функции БС
Функция ПС
Фирме потребуется 5 млн рублей через 12 лет. В настоящее время фирма располагает деньгами и готова положить их на депозит единым вкладом, чтобы через 12 лет он достиг 5 млн рублей. Определить необходимую сумму текущего вклада, если ставка процента по нему составит 12 % годовых.
Решение
Так как в задаче не указан период начисления процентов, то по умолчанию они начисляются раз в год. Решение задачи представлено на рисунке 29.
 |
Рис. 29. Решение задачи с использованием функции ПС
Функция КПЕР
Рассчитать, через сколько лет вклад размером 1000 руб. достигнет 1 млн руб., если годовая ставка составляет 16,79 % и начисление процентов производится ежеквартально.
Решение
При решении дано задачи нужно помнить, что ответ исчисляется в периодах задачи – числе кварталов, и его мы делим на 4, чтобы определить число лет. Решение задачи проиллюстрировано на рисунке 30.
 |
Рис. 30. Решение задачи с использованием функции КПЕР
Функция СТАВКА
Предположим, компании Х потребуется 100 000 рублей через 2 года. Компания готова вложить 5000 рублей сразу и вкладывать по 2500 рублей каждый последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года?
Решение
Решение задачи представлено на рисунке 31. Важно помнить, что ответ по функции КПЕР получится в периодах задачи – процентной ставке за месяц (т. к. поступления производились ежемесячно), которую затем надо перевести в годовую ставку.
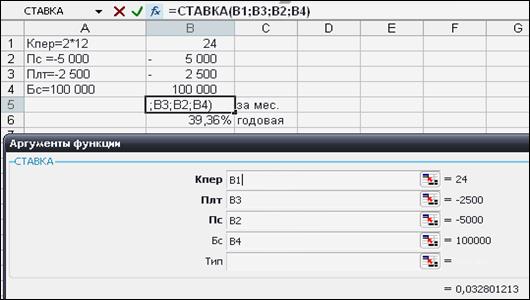 |
Рис. 31. Решение задачи с использованием функции СТАВКА
Функция ПЛТ
Предположим, что необходимо накопить 4000 рублей за три года, откладывая постоянную сумму в начале каждого месяца. Какой должна быть эта сумма, если процент по вкладу составляет 12 % годовых?
|
|
|
Решение
Обратим внимание на платежи пренумерандо и поставим тип, равный 1. Заметим, что аргумент Бс всегда вносится со знаком «+». Решение задачи показано на рисунке 32.
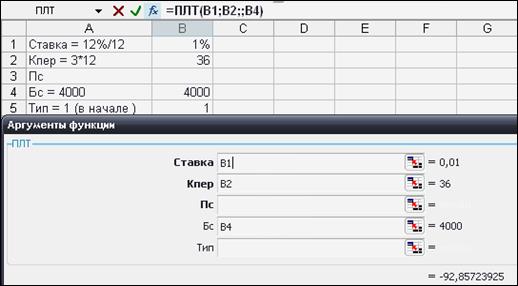
Рис. 32. Решение задачи с использованием функции ПЛТ
|
|
|


