Практическое занятие 2 «Оптимизационные модели»

Задачи: научить студентов строить оптимизационные модели.

Используемое программное обеспечение: операционная система Windows, Ms Excel, надстройка Поиск решения.

Время выполнения работы: 6 часов аудиторных занятий.

 

Формулировка любой оптимизационной задачи требует использо­вания некоторой базовой системы понятий.

Любая переменная (изменяемая ячейка в электронной таблице) обычно интерпре­тируется как некоторый ресурс (например, ресурс времени, материа­ла, продукта, валюты), выраженный в количественном измерении (минуты, тонны, штуки, рубли).

Задача оптимизации состоит в том, чтобы подобрать такие значения переменных, при которых целевая функция (целевая ячейка таблицы) принимает максимальное, минималь­ное или заданное значение (оптимальное значение), при этом най­денные значения переменных в совокупности составляют оптималь­ное решение задачи.

В классическом исследовании операций задачи матема­тического программирования делятся на несколько различных типов в зависимости от вида целевой функции и ограничений. К основным типам относятся задачи линейного и нелинейного программирования.

Для первого типа характерна целевая функция, линейно зависящая от пе­ременных (ресурсов) исследуемой системы, и такие же линейные ограничения.

Если же целевая функция или хотя бы одно из ограни­чений нелинейно зависит от переменной (хотя бы одной), задача от­носится к типу нелинейного программирования.

В качестве примеров нелинейностей можно привести зависимости видов 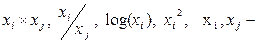это переменные задачи.

Если оптимизационная задача должна решаться в целых числах, когда хотя бы одна из переменных модели должна измеряться в шту­ках, говорят о целочисленном программиро­вании. Наконец, если хотя бы одна из переменных может принимать только одно из двух значений (0 или 1), говорят о булевском програм­мировании.

Ниже мы рассмотрим задачи линейного программирования.

Общая задача линейной оптимизации заключается в нахождении максимума (минимума) линейной целевой функции f(x):

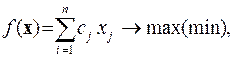(1)

 

 

при ограничениях

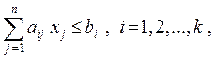(2)

 

, (3)

. (4)

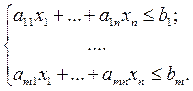Систему ограничений на задачу можно представить следующим образом:

 

(5)

 

 

Набор чисел 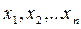, удовлетворяющий ограничениям задачи линейного программирования, называется ее планом.

Первым этапом формализации модели линейного программирования (ЛП) должно стать выявление ограничений на переменные решения. Ограничения сужают множество допустимых значений. Примерами ограничений могут быть:

– инвестиции в проект ограничены суммой капитала, имеющегося в распоряжении;

– решения директора завода ограничены производственной мощностью завода и имеющимися ресурсами;

– план выпуска изделий ограничен имеющимися ресурсами материалов и спросом на данный вид продукции.

Целевая функция или показатель эффективности, который можно минимизировать (затраты или время) или максимизировать (прибыль, эффективность, производительность), существует в каждой модели линейного программирования. При реализации задачи ЛП средствами Excel можно использовать следующие рекомендации:

– каждая переменная решения располагается в отдельной ячейке, ячейки группируются по строкам или столбцам; каждому ограничению отводится отдельная строка или столбец (чаще всего переменные решения располагаются в столбцах, а ограничения – в строках);

– коэффициенты целевой функции хранятся в отдельной строке, а формула для вычислений целевой функции находится в соседней ячейке.

Надстройка Excel Поиск решения позволяет оптимизировать как линейные, так и нелинейные модели, но необходимо помнить, что при линейных моделях все формулы, содержащие переменные, должны быть линейными. Рассмотрим несколько примеров задач ЛП.

 

Задача составления скользящих графиков

Такие графики обычно связаны с расписаниями многосменной работы предприятия в условиях нестационарного спроса на товары или услуги, связанные с деятельностью этого предприятия. Задача состоит в том, чтобы организовать распи­сание обслуживания клиентов та­ким образом, чтобы издержки от неравномерности спроса были бы минимальны.

В таблице 2 приведено число продавцов, необходимое для удовлетворения покупательского спроса в зале магазина. Требуется так организовать расписание работы про­давцов, чтобы их общее количество (то есть расходы на оплату их труда) было минимальным.

Пусть продавцы в магазине работают по 8 часов. В соответствии с данными задачи, число продав­цов меняется через 4 часа. Если предположить, что в первую смену работает x₁ продавцов, во вторую — x₂ и т. д., то график работы про­давцов представим на рисунке 3.

Таблица 2

Требуемое количество продавцов

Время суток	0–4	4–8	8–12	12–16	16–20	20–24
Требуемое кол-во продавцов

 

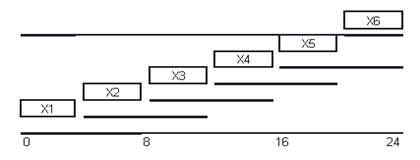
Рис. 3. График работы продавцов

Жирные линии – это смены, они начинаются через 4 часа и продолжаются 8 часов. Смены перекрываются, т. е., с 4 до 8 часов в зале присутствуют (x₁ + x₂) продав­цов, с 8 до 12 часов — (x₂ + x_З) продавцов, а с 0 часов до 4 работа­ют (x₁ + x₆) продавцов. Этот «скользящий» график и образует рас­писание смен. 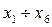определяют изменяемые переменные, кото­рые следует определять из условия минимального общего количества продавцов, т. е. целевая функция в этой задаче определяется выраже­нием: .

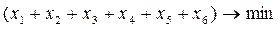В качестве ограничений при этом будут выступать условия:

x₁+x₆ >= 2; x₁+x₂ >= 2; x₂+x₃ >= 5; x₃+x₄ >= 7; x₄+x₅ >= 7; x₅+x₆ >= 4.

Кроме того, 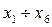должны быть целыми и положительными. Задача представлена на рисунке 4.

 

 

 

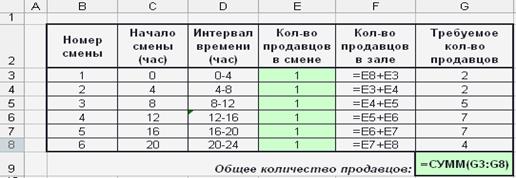Рис. 4. Модель задачи составления скользящих графиков

Задача оптимизации инвестиций

Основная цель решения этого класса задач — найти оптимальное распределение финансовых средств, доставляющее макси­мальную прибыль по истечении срока действия инвести­ционного проекта.

Денежные средства могут быть использованы для финансирования двух проектов. Проект А гарантирует получение прибыли в размере 70 центов на вложенный доллар через год. Проект В гарантирует получение прибыли в размере 2 долларов на каждый инвестированный доллар, но через два года. При финансировании проекта В период инвестиций должен быть кратным двум годам. Как следует распорядиться капиталом в 100 000 долларов, чтобы максимизировать суммарную величину прибыли, которую можно получить через три года после начала инвестиций?

Содержимое изменяемых ячеек:

x_а, Y_a — вложения в проект A; X_b, Y_b — вложения в проект В.

Возможные инвестиции могут быть проиллюстрированы схемой, приведенной на рисунке 5.

Из схемы следует, что в исследуемой системе суще­ствуют только два возможных срока вложений — начало первого года и начало второго года. Суммы вложений в эти сроки определяют со­держимое изменяемых ячеек. «Точка вложений» в начале третьего года одна, в нее вкладываются все доходы от предыдущих вложений.

 

Рис. 5. Схема инвестиций в проекты А и В

Ограничения:

x_а + x_Ь = 100 000; y_a + y_b = (1 + 0,7)*x_а.

Целевая функция:

z= y_a*(l + 0,7)*2 + y_b*(l + 2) + x_b*(l + 2)*(1 + 0,7)® max.

 

 

Решение задачи представлено на рисунке 6.

 

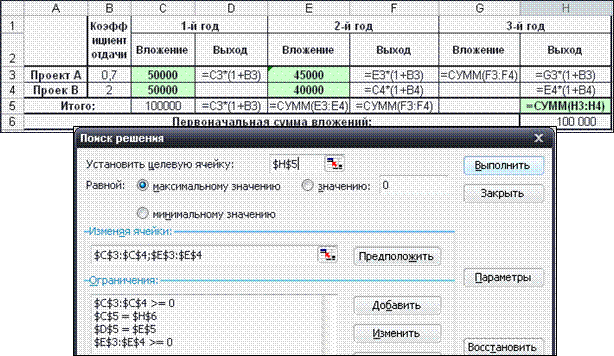Рис. 6. Модель задачи об инвестициях

Задача логического выбора

Этот класс задач связан с выбором конкретных вариантов органи­зации системы с учетом ресурсных ограничений. Как правило, в них используются изменяемые ячейки, которые могут хранить одно из двух значений: 1 или 0.

Выбор одного из двух вариантов организации исследу­емой системы (1, 2) может определяться двумя булевскими перемен­ными (х_I, х₂). Условие выбора только одного из двух вариантов эквивалентно логическому ограничению: х_I+х₂= 1. Такое ограничение моделирует условие взаимоисключения. Условие выбора хотя бы одного из двух вариантов эквивалентно логическому ограничению х_I+х₂ >= 1.

Если вариант 2 может быть принят только при принятии
вари­анта 1, следует использовать ограничение х ₁ >= х ₂. Если же вариант 2 принимается при принятии варианта 1, то вводится ограничение х ₂ >= х _I. В качестве примера рассмотрим задачу выбора варианта капиталовложений.

Рассматриваются пять проектов, которые могут быть осуществле­ны в течение трех лет. Ожидаемые величины прибыли от реализации проектов и распределение необходимых ка­питаловложений по годам (в тыс. долл.) приведены в таблице 3. Требуется выбрать совокупность проектов, кото­рой соответствует максимум общей прибыли.

Таблица 3

Исходные данные задачи выбора проектов

Проект	Распределение капиталовложений	Прибыль
Год 1	Год 2	Год 3
Max объем вложений

Добавим к таблице исходных данных столбец изменяемых ячеек. Обозначим содержимое этих ячеек как х _i, где i определя­ет номер проекта, a х_i – решение: вкладывать (х_i =1) или нет (х_i = 0) средства в i-ый проект (рис. 7). Ограничениями задачи будут:

– По объему капиталовложений

в первый год: 5* x_I + 4*x₂ +3*x_З + 7*x₄ + 8*x₅ <= 25;

во второй год: 1* x_I + 7*x₂ +9*x_З + 4*x₄ + 6*x₅ <= 25;

в третий год: 8* x_I + 10*x₂ +2*x_З + 10*x₄ + 1*x₅ <= 25.

– «Естественные» ограничения: 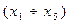– двоичные (булевские).

– Целевая функция: Z= 20*x ₁ + 40*x ₂ + 20*x _З + 15*x ₄ + 30*x ₅ ® max.

 

 

 

 

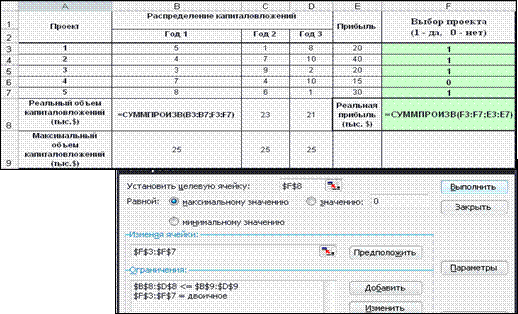Рис. 7. Модель задачи логического выбора

Задачи для самостоятельной работы

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: