Диаграммы состояния однокомпонентных (унарных) систем

Кафедра общей и физической химии

 

Физическая химия

Фазовые диаграммы

 

Учебное пособие

 

 

Санкт-Петербург

УДК 541.1.076 (075.83)

ББК

Авторский знак

 

 

Физическая химия. Фазовые диаграммы. Составители: Д.Э. Чиркст, О.В. Черемисина, И.И. Иванов, О.Л. Лобачева, Т.Е. Литвинова, Н.В. Джевага.

 

Изложены основы построения и чтения фазовых диаграмм одно-, двух- и трехкомпонентных систем, включая водно-солевые системы. Приведены примеры типовых диаграмм состояния; описана последовательность их решения, даны примеры решения фазовых диаграмм. Учебное пособие предназначено для аудиторных и самостоятельных занятий по дисциплинам «Химия», «Физическая химия», «Физическая и коллоидная химия» для студентов направлений 130301, 130302, 130306, 130405, 130603, 150102, 150103, 220301, 240403, 280202.

Введение

При изучении свойств гетерогенных систем широко используется метод, получивший название физико-химический анализ и основанный на графическом изображении зависимости между составом и свойствами системы с помощью диаграмм состояния. В большинстве случаев они строятся по экспериментальным данным (например, по кривым охлаждения) с применением специальной техники исследования и позволяют изучать до 140 различных физических и химических свойств системы.

Наиболее распространены диаграммы состояния, характеризующие зависимость между исходным составом систем и температурой фазовых превращений, протекающих в этих системах. Изучение подобных диаграмм позволяет легко определить взаимную растворимость компонентов системы в различных агрегатных состояниях, наличие у них полиморфных превращений, состав и свойства химических соединений, образованных компонентами, температуру всех фазовых превращений в системах заданного состава, изменение состава и относительного количества находящихся в равновесии фаз при изменении температуры, выбрать состав наиболее легкоплавкой или тугоплавкой системы и т.д.

Наглядность и высокая информативность диаграмм состояния обусловили их широкое применение в прикладных науках: химической технологии, петрологии, минералогии, гидрогеологии, металлургии, металловедении.

Основные понятия и определения

Гетерогенной (неоднородной) называется термодинамическая система, состоящая из нескольких фаз, между которыми имеются границы раздела. Фаза – совокупность гомогенных частей системы, одинаковых по составу, физическим и химическим свойствам, и отделенных от других частей системы поверхностью раздела. Каждая фаза может содержать одно или несколько составляющих веществ. Составляющее вещество – любое вещество, которое может быть выделено из системы и способно существовать вне ее. Следует различать понятия составляющее вещество и компонент системы.

Компоненты системы (независимые составляющие вещества) – составляющие ее вещества, концентрации которых в данной системе могут быть выбраны произвольно без изменения числа фаз системы. Посредством компонентов системы полностью можно задать ее вещественный и фазовый состав.

Число компонентов системы – наименьшее число составляющих веществ, достаточное для определения состава любой фазы системы. Число компонентов (К) равняется числу составляющих веществ системы (С.В.) за вычетом числа уравнений (У), связывающих концентрации этих веществ на момент равновесия:

.

Таким образом, число компонентов системы или совпадает с числом составляющих веществ или меньше его.

Если между составляющими веществами отсутствует химическое взаимодействие, то уравнений связи нет, и число компонентов равно числу составляющих веществ.

Если в системе протекают химические реакции, то количества составляющих веществ зависят друг от друга, и состав системы можно определить по содержанию лишь части составляющих систему веществ, т.е. по компонентам системы.

Пример 1. При протекании гомогенной реакции образования йодистого водорода составляющие вещества равновесной системы (H₂, I₂ и HI) связаны между собой уравнением константы равновесия:

.

В состоянии равновесия состав системы можно описать, задав парциальные давления и или и ; содержание третьего вещества всегда можно вычислить по уравнению константы равновесия. В этом случае K = 3 – 1(уравнение константы) = 2

Если проводить разложение йодистого водорода, появляется дополнительное условие и K = 3 – 2 = 1.

Пример 2. При образовании кристаллического хлорида аммония по уравнению реакции:

.

В равновесной системе число составляющих веществ равно трем.

Концентрации аммиака и хлороводорода связаны уравнением баланса масс:

.

В этой ситуации число компонентов системы K = 3 – 1 = 2.

При термическом разложении кристаллического хлорида аммония по реакции

.

В равновесной системе будет три составляющих вещества: NH₃, HCl и NH₄Cl. Концентрации газообразных веществ связаны уравнением баланса масс

и равенством давлений хлороводорода и аммиака, которое определяется уравнением реакции: .

В этом случае система будет однокомпонентной и K = 3 – 2 = 1.

По числу компонентов различают диаграммы состояния одно-, двух-, трех- и т. д. компонентных систем.

Важной характеристикой любой термодинамической системы является ее число степеней свободы, т.е. число независимых переменных (давление, температура, состав), которые можно свободно менять в определенных пределах, и при этом количество и природа фаз останутся без изменений.

Число степеней свободы определяется правилом фаз Гиббса:

,

где п – количество параметров состояния системы, изменение которых приводит в определенных условиях к изменению фазового состава системы.

Правило фаз Гиббса является наиболее общим и точным законом, определяющим условия равновесия в гетерогенной системе. Число фаз всегда меньше суммы числа компонентов и внешних сил (параметров): .

Число степеней свободы равновесной термодинамической системы, на которую влияют только температура и давление (n = 2) определяется уравнением:

.

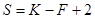Если в число внешних факторов входит либо температура Т, либо давление Р, то

.

Если число степеней свободы S = 0, то такая система называется инвариантной. Безвариантной системе соответствует максимально возможное количество фаз, находящихся в равновесии.

Если число степеней свободы S = 1, то такая система называется моновариантной; в ней возможно изменение только одного параметра.

Правило фаз позволяет:

1) определить возможное число степеней свободы системы с заданным числом компонентов в зависимости от числа находящихся в равновесии фаз,

2) вычислить максимальное число фаз, которое может находиться в равновесии в данной системе и соответствует безвариантному состоянию (S = 0), в котором все параметры состояния системы (состав, температура и давление) имеют строго определенные фиксированные значения.

Диаграммы состояния однокомпонентных (унарных) систем

Диаграммы состояния однокомпонентных систем отражают свойства одного вещества, простого или сложного, химический состав которого постоянен, и на свойства которого влияют лишь внешние независимые переменные (температура и давление).

Диаграммы состояния таких систем могут быть изображены на плоскости в координатах Р - Т или P - V, где V - объем. Максимальное число фаз, находящихся в равновесии в однокомпонентных системах, в соответствии с правилом фаз Гиббса равно трем:

при n = 1 и S = 0 .

Эти фазы могут сосуществовать лишь при строго фиксированных параметрах, поскольку система при этом не имеет степеней свободы.

На рис. 1 в качестве примера изображена простейшая объемная диаграмма состояния углекислого газа, а также ее проекции в координатах P - V, T - V и Р - Т.

Рис. 1. Объемная диаграмма состояния углекислого газа и ее проекции на плоскости P - T (a), T – V (б) и P – V (г).

На практике чаще всего применяется диаграмма состояния, построенная в координатах давление - температура, показанная на рис. 2.

Рис. 2. Плоская диаграмма состояния углекислого газа, построенная в координатах P - T.

Линии ОА, ОK и ОВ разделяют диаграмму на три поля, показывающие области существования, т.е. пределы температур и давлений, трех устойчивых агрегатных состояний вещества: твердого, жидкого и газообразного. В каждом из этих состояний система имеет две степени свободы.

На линиях диаграммы в равновесии находятся две фазы: на линии испарения (конденсации) ОK – газ и жидкость, на линии плавления (кристаллизации) ОА – жидкая и твердая фазы, а на линии возгонки (сублимации) ОВ – твердая фаза и пары. Каждая линия диаграммы показывает взаимосвязь температуры соответствующего фазового превращения и внешнего давления или давления насыщенного пара.

Линия OD показывает область существования метастабильной фазы. В данном случае – переохлажденной жидкости, т.к. линию OD можно представить как продолжение линии ОА. Подобные штриховые линии часто можно видеть также на диаграммах состояния компонентов, представленных различными кристаллическими модификациями. Переход одной модификации в другую обычно происходит очень медленно и сопровождается поэтому длительным сохранением метастабильных при данных параметрах твердых фаз, переходящих в устойчивые фазы лишь после длительной выдержки.

Наклон граничных линий определяется соотношением плотностей фаз, находящихся в равновесии.

Ход линий диаграммы описывается уравнением Клапейрона-Клаузиуса, которое в дифференциальной форме имеет вид:

,

где Δ _trH – изменение энтальпии (теплота) фазового перехода, Дж/моль; T_tr – температура фазового перехода, K; Δ V – изменение молярного объема в процессе фазового перехода, м³/моль, М – молярная масса вещества, кг/моль; d_k и d_i – плотности вещества в исходном и конечном фазовом состояниях, кг/м³.

При испарении, плавлении или возгонке веществ и других процессах, протекающих с поглощением тепла, т.е. при Δ _trH > 0, знак производной d T /d P, определяющий наклон кривых на диаграмме, зависит только от знака разности плотностей исходной и конечной фаз.

Если , то d T /d P > 0 (рис. 3, а), и с ростом давления температура фазового превращения увеличивается.

Если , то d T /d P < 0 (рис. 3, б), и с ростом давления температура фазового превращения уменьшается.

Рис. 3. Наклон кривых фазовых переходов в зависимости от соотношения плотностей фаз:

а) ; б) .

Точка О, в которой пересекаются три линии фазовых переходов, называется тройной точкой, показывающей температуру Т ₀ и давление Р ₀, при которых могут сосуществовать в безвариантном равновесии одновременно три фазы.

Пользуясь диаграммами состояния можно проследить за всеми изменениями свойств системы при изменении параметров ее состояния. Например, на диаграмме (см. рис. 2) видно, что при внешнем постоянном давлении P_i в точке 1 вещество находится в твердом состоянии, причем давление насыщенных паров над твердой фазой при заданной температуре равно Р _тв. При нагревании вещества при заданном постоянном давлении фигуративная точка системы перемещается по горизонтальной прямой вправо, и в точке 2 происходит его плавление. Температура при этом остается постоянной, так как по правилу фаз Гиббса число степеней свободы двух фаз S = l + l – 2 = 0 до тех пор, пока одна из фаз полностью не превратится в другую, в данном случае твердая в жидкую. Далее от точки 2 до точки 4 нагревается жидкая фаза, при этом непрерывно возрастает по линии ОК давление ее насыщенного пара. В точке 3 его величина равна Р _ж, а в точке 4 становится равным внешнему давлению P_i. При температуре, отвечающей точке 4, начинается и заканчивается (F = 0) кипение жидкости, после чего остается одна фаза – газ, система приобретает одну степень свободы, температура газа растет. Линия испарения ОК на диаграмме обрывается в критической точке K, которой соответствуют критические параметры: критическое давление Р _кр и критическая температура Т _кр.

При охлаждении пара при том же постоянном давлении P_i в точке 4 происходит его конденсация, далее охлаждается жидкость, которая в точке 2 должна закристаллизоваться или перейти в метастабильное состояние в виде переохлажденной жидкости с последующей ее кристаллизацией.

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: