Оборудование, технические и инструментальные средства

 

Для выполнения работы необходим персональный компьютер с установленной операционной системой MsWindows. Используется программа для ПК «ЛАБ3. Виртуальная лабораторная работа №3 по дисциплине МИОУ. Статистическая оценка параметров распределения случайных величин. Проверка гипотез»

 

Описание хода выполнения работы. Исходные данные.

 

1) Запустили программу ЛАБ3, зарегистрировались используя номер своей зачетной книжки.

2) Выбрали исследуемые случайные величины QA и Y.

3) Зарегистрировали показания (12-18 значений) обоих случайных величин.

4) Выполнили все необходимые расчеты с использование систем MsExcel и Mathcad

 

Таблица 3.1 - Исходные данные

X	Y	X	Y	X	Y
40,76	44,93	49,37	35,23	36,84	46,48
34,98	49,57	61,31	31,53	23,24	59,54
71,96	24,92	36,89	46,84	54,44	31,69
62,49	30,69	25,98	58,14	54,76	33,9
67,37	29,39	38,44	46,22	41,82	40,83

 

Результаты выполнения

 

Требуется определить оценки параметров распределения (математическое ожидание, дисперсию, коэффициент корреляции, доверительные интервалы для среднего и для дисперсии), а также проверить статистические гипотезы.

При расчетах за уровень значимости α принималась величина равная 0.05, а при определении границ доверительного интервала для дисперсии - 0.04.

1. Для случайной величины X:

= 46.71 σ_X² = 221.2801

Доверительный интервал для среднего: [38,45221; 54,96779]

Доверительный интервал для дисперсии: [115,1643; 516,3202]

2. Для случайной величины Y:

= 40,66 σ_Y²=112,5568

Доверительный интервал для среднего: [34,7705; 46,5495]

Доверительный интервал для дисперсии: [58,57973; 262,6325]

3. Коэффициент корреляции R_xy:

R_xy = -0.97736

4. Проверка гипотезы о равенстве Х числу 80:

t = -8,66739, t_kp(α,  n-1)=2.15, так как |t|>t_kp, гипотеза отвергается.

5. Проверка гипотезы о равенстве Y числу 40:

t = 0,240937, t_kp(α, n-1)=2.15, так как |t|<t_kp, гипотеза принимается.

6. Проверка гипотезы о равенстве математических ожиданий:

t = 1,282431, t_kp(α, 2·n-2)=2.04, так как |t|<t_kp, гипотеза принимается.

7. Проверка гипотезы о равенстве дисперсий:

f = 1,965942, tkp(α, n-1,n-1)=2.5, так как |t|<tkp, гипотеза принимается.

8. Проверка гипотезы об отсутствии корреляции между случайными величинами X и Y:

t = -16,6557, tkp(α, n-2)=2.16, так как |t|>tkp, гипотеза отвергается.

На рисунке 3.1 показано корреляционное поле – корреляция между X и Y.

 

Рисунок 3.1 – Корреляция между X и Y (корреляционное поле)

Выводы

 

В результате проделанной работы и выполненных расчетов, мы проверили гипотезы, часть из них приняли и часть отвергли. Понятие статистической гипотезы означает предположение о виде распределения СВ или о некотором параметре ее распределения. Проверка гипотезы заключается в сопоставлении определенного статистического показателя (критерия значимости), вычисленного по данной выборке, с критерием значимости, найденным теоретически при условии, что проверяемая гипотеза верна.

Лабораторная работа №4. «Планирование эксперимента»

Цели и задачи работы

 

Целью работы является определение параметров регрессионной модели методами активного эксперимента с использованием планирования экспериментов. А также научиться применять знания, полученные при изучении темы «Определение параметров регрессионной модели. Построение моделей статики объекта управления по данным активного эксперимента (методы планирования эксперимента)»

Содержание работы. Теоретические основы

 

Общий вид схемы дисперсионного и регрессионного анализа планированного эксперимента, когда каждый опыт в матрице планирования повторяется m раз следующий:

Линейный план 2^К

 

Таблица 4.1 – План эксперимента

№ оп.	x0	x1	x2	...	xk	Y		σY2
	+1	+1	-1	.	+1	y11,y12,...,y1m	y1	σ12
	+1	-1	-1	.	+1	y21,y22,...,y2m	y2	σ22
	+1	+1	+1	.	+1	y31,y32,...,y3m	y3	σ32
.	.	.	.	.		.	.
.	.	.	.	.		.	.
.	.	.	.	.		.	.
N	+1	-1	+1	.	-1	yN1,yN2,...,yNm	y4	σN2

 

1) Проводятся необходимые эксперименты.

2) Проверяется однородность выборочных дисперсий по критерию Кохрена. Для этого составляется отношение максимальной дисперсии к сумме всех дисперсий:

 

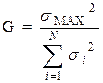
Полученное отношение сравнивают с табличным: Gкр=G(α, f₁, f₂), где: α=0.05, f₁ = m - 1, f₂ = N. 0Если G<Gkp дисперсии однородны.

Тогда в качестве дисперсии воспроизводимости можно взять среднюю дисперсию:

 

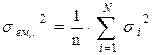
(4.3)

 

 

с числом степеней свободы f_вос = N(m-1)

3) Коэффициенты уравнения регрессии определяются по формуле:

 

 

(4.4)

 

 

4) Дисперсия коэффициентов определяется следующим образом:

 

σ_Bj² = σ_ВОС²/(N·m) (4.5)

 

5) Значимость коэффициентов проверяется по критерию Стьюдента. Для всех коэффициентов уравнения регрессии составляется t-отношение:

 

t_j = |b_j|/σ_Bj (4.6)

 

которое сравнивают с табличным tkp=t(α, f) для уровня значимости σ =0.05 и числа степеней свободы f=N(m-1). Если t_j < tkp, то соответствующий коэффициент b_j отсеивается как незначимый из уравнения регрессии.

6) Адекватность уравнения регрессии эксперименту проверяется по критерию Фишера. Для проверки дисперсии составляется дисперсионное отношение:

 

F = σ_АД²/σ_ВОС²

 

где σ_АД² - дисперсия адекватности, определяемая по формуле:

 

 

 

(4.7)

 

l - число значимых коэффициентов уравнения регрессии.

Если полученное дисперсионное отношение оказывается меньше табличного Fkp=F(α, f_ад, f_вос), где α =0.05, f_ад=N - l, f_вос=N(m-1), то уравнение адекватно эксперименту, в противном случае для адекватного описания эксперимента необходимо увеличить порядок аппроксимирующего полинома.

Ортогональный план 2 порядка

 

Таблица 4.2 - Ортогональный план 2 порядка

№ оп	x0	x1	x2	.	xk	x1'	x2'	.	xk'	Y		σY2
	+1	+1	-1	.	+1	x11'	x21'	.	xk1'	y11,y12,..,y1m	y1	σ12
	+1	-1	-1	.	+1	x12'	x22'	.	xk2'	y21,y22,..,y2m	y2	σ22
	+1	+1	+1	.	+1	x13'	x23'	.	xk3'	y31,y32,,y3m	y3	σ32
.	.	.	.	.		.	.	.	.	.	.	-
.	.	.	.	.		.	.	.	.	.	.	-
.	.	.	.	.		.	.	.	.	.	.	-
N	+1	-1	+1	.	-1	x1N'	x2N'	.	xkN'	yN1,yN2,,yNm	yN	σN2
N+1	+a			.		.	.	.	.	.	.	-
N+2	-a			.		.	.	.	.	.	.	-
N+3		+a		.		.	.	.	.	.	.	-
N+4		-a		.		.	.	.	.	.	.	-
N+5			+a	.		.	.	.	.	.	.	-
N+6			-a	.		.	.	.	.	.	.	-
.	.	.	.	.	.	.	.	.	.	.	.	-
.					+a	.	.	.	.	.	.	-
N+2·k					-a	.	.	.	.	.	.	-
N+2·k+1						x1n'	x2n'	.	x3n'	yn1,yn2,,ynm	yn	σn2

 

Количество опытов определяется как 2^k + 2·k + 1

Основу плана составляет линейный план 2^k (строки с 1 по N). Кроме того проводятся опыты в звездных точках (строки с N+1 по N+2·k) и в центре плана (строка N+2·k+1).

Столбцы X_j' определяются по формуле:

 

 

(4.8)

 

 

1)Среднее значение измеряемой величины и дисперсия определяются по формулам (4.1), (4.2).

2) Проверяется однородность выборочных дисперсий по критерию Кохрена. Дисперсия воспроизводимости рассчитывается по (4.3).

3) Коэффициенты уравнения регрессии определяются по формуле:

 

 

(4.9)

 

 

5) Дисперсия коэффициентов определяется следующим образом:

 

 

(4.10)

 

 

5) Методика проверки на значимость коэффициентов описана выше (см. формулы (4.6)).

6) Проверка адекватности уравнения регрессии эксперименту описана выше (см. формулы (4.7)).

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: