 |
Оборудование, технические и инструментальные средства
|
|
|
|
Для выполнения работы необходим персональный компьютер с установленной операционной системой MsWindows. Используются программы для ПК «ЛАБ5. Виртуальная лабораторная работа №5 по дисциплине МИОУ. Исследование динамики объектов управления» и «Оценивание состояния системы дискретным фильтром Калмана»
Описание хода выполнения работы.
Порядок ручного счета следующий:
1. Запустили программу ЛАБ5, зарегистрировались, используя номер своей зачетной книжки.
2. Выбрали канал воздействия и возмущение на входе
3. Провели эксперимент по снятию кривой разгона.
4. Разбили участок кривой разгона от момента времени t= 
до t=tk не менее, чем на 15-20 равных частей. В дальнейшем принимают момент времени t= за начало отсчета, то есть за точку t=0. Шаг разбиения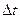 
выбирается таким, чтобы в его пределах кривая X(t) мало отличалась от прямой. Для того, чтобы обеспечить достаточную точность измерения, участок кривой, лежащий внутри прямоугольника АВСД на рисунке 1б, вычерчивается на листе миллиметровой бумаги не менее, чем формата A4.
5. Выполнили все необходимые расчеты с использование систем MsExcel и Mathcad.
6. Заполнили столбцы 1 и 2 таблицы 1. Обратим внимание, что t1=0 и X1=0.
7. Заполнили столбец 3, используя формулу (5.4).
8. Определили S1 как сумму столбца 3.
9. Определили F1 по формуле (5.9).
10.Заполнили столбец 4, используя формулу (5.18).
11.Заполнили столбцы 5 и 6.
12.Определили S2, как сумму столбца 6.
13.Рассчитали F2 по формуле (5.10).
14.Заполнили столбцы 7, 8.
15.Определили S3, как сумму столбца 8.
16.Рассчитали F3 по формуле (5.11).
17.В соответствии с приведенными выше условиями определили вид передаточной функции и значения коэффициентов.
18.Определили значения С, .
|
|
|
19.Записали значение передаточной функции в размерном виде (5.1) с подстановкой всех численных значений. Проверили адекватность полученной математической модели объекта
20.Запустили программу ЛАБ5, зарегистрировались, используя номер своей зачетной книжки.
21.Выбрали другой канал воздействия и возмущение на входе
22.Повторили все действия описанные выше
23.Выполнили все необходимые расчеты с использование систем MsExcel и Mathcad
Результаты выполнения
Исследование главного канала регулирования:
В результате эксперимента были получены следующие исходные данные по каналу «Возмущение регулирующего органа, ΔU(%)-Температура пара, Т»
Таблица 5.3 – Результаты эксперимента - главный канал регулирования
| Время - t | Выход - X | ΔX |
| 57,47 | ||
| 57,47 | 0,651 | |
| 57,472 | 1,406 | |
| 57,86 | 2,01 | |
| 58,511 | 2,601 | |
| 59,266 | 2,792 | |
| 59,87 | 3,434 | |
| 60,461 | 3,745 | |
| 60,652 | 3,895 | |
| 61,294 | 4,074 | |
| 61,605 | 4,218 | |
| 61,755 | 4,37 | |
| 61,934 | 4,457 | |
| 62,078 | 4,521 | |
| 62,23 | 4,545 | |
| 62,317 | 4,611 | |
| 62,381 | 4,627 | |
| 62,405 | 4,654 | |
| 62,471 | 4,676 | |
| 62,487 | 4,689 | |
| 62,514 | 4,703 | |
| 62,536 | 4,712 | |
| 62,549 | 4,72 | |
| 62,563 | 4,728 | |
| 62,572 | 4,732 | |
| 62,58 | 4,735 | |
| 62,588 | 4,738 | |
| 62,592 | 4,742 | |
| 62,595 | 4,742 | |
| 62,598 | 4,742 | |
| 62,602 | 4,742 |
Получение математической модели методом площадей
Таблица 5.4 – Результаты расчетов
| t | ΔX | Z | Q | 1-Q | Z(1-Q) | (1-2Q+Q^2/2) | Z(1-2Q+Q^2/2) | Xрасч |
| 5E-16 | ||||||||
| 0,651 | 0,8627 | 0,20965 | 0,79035 | 0,68185 | 0,602682 | 0,5199 | 0,224 | |
| 1,406 | 0,7035 | 0,41929 | 0,58071 | 0,40853 | 0,249316 | 0,1754 | 0,939 | |
| 2,01 | 0,5761 | 0,62894 | 0,37106 | 0,21378 | -0,060098 | -0,035 | 1,753 | |
| 2,601 | 0,4515 | 0,83859 | 0,16141 | 0,07288 | -0,32556 | -0,147 | 2,445 | |
| 2,792 | 0,4112 | 1,04823 | -0,0482 | -0,0198 | -0,547071 | -0,225 | 2,983 | |
| 3,434 | 0,2758 | 1,25788 | -0,2579 | -0,0711 | -0,724629 | -0,2 | 3,393 | |
| 3,745 | 0,2102 | 1,46753 | -0,4675 | -0,0983 | -0,858236 | -0,18 | 3,707 | |
| 3,895 | 0,1786 | 1,67717 | -0,6772 | -0,121 | -0,947892 | -0,169 | 3,947 | |
| 4,074 | 0,1409 | 1,88682 | -0,8868 | -0,1249 | -0,993595 | -0,14 | 4,131 | |
| 4,218 | 0,1105 | 2,09647 | -1,0965 | -0,1212 | -0,995347 | -0,11 | 4,273 | |
| 4,37 | 0,0784 | 2,30611 | -1,3061 | -0,1025 | -0,953147 | -0,075 | 4,382 | |
| 4,457 | 0,0601 | 2,51576 | -1,5158 | -0,0911 | -0,866995 | -0,052 | 4,465 | |
| 4,521 | 0,0466 | 2,72541 | -1,7254 | -0,0804 | -0,736892 | -0,034 | 4,53 | |
| 4,545 | 0,0415 | 2,93505 | -1,9351 | -0,0804 | -0,562836 | -0,023 | 4,579 | |
| 4,611 | 0,0276 | 3,1447 | -2,1447 | -0,0592 | -0,344829 | -0,01 | 4,617 | |
| 4,627 | 0,0243 | 3,35435 | -2,3543 | -0,0571 | -0,082871 | -0,002 | 4,646 | |
| 4,654 | 0,0186 | 3,56399 | -2,564 | -0,0476 | 0,22304 | 0,0041 | 4,668 | |
| 4,676 | 0,0139 | 3,77364 | -2,7736 | -0,0386 | 0,572902 | 0,008 | 4,685 | |
| 4,689 | 0,0112 | 3,98329 | -2,9833 | -0,0333 | 0,966716 | 0,0108 | 4,698 | |
| 4,703 | 0,0082 | 4,19294 | -3,1929 | -0,0263 | 1,404482 | 0,0116 | 4,709 | |
| 4,712 | 0,0063 | 4,40258 | -3,4026 | -0,0215 | 1,8862 | 0,0119 | 4,716 | |
| 4,72 | 0,0046 | 4,61223 | -3,6122 | -0,0168 | 2,411869 | 0,0112 | 4,722 | |
| 4,728 | 0,003 | 4,82188 | -3,8219 | -0,0113 | 2,98149 | 0,0088 | 4,727 | |
| 4,732 | 0,0021 | 5,03152 | -4,0315 | -0,0085 | 3,595063 | 0,0076 | 4,73 | |
| 4,735 | 0,0015 | 5,24117 | -4,2412 | -0,0063 | 4,252588 | 0,0063 | 4,733 | |
| 4,738 | 0,0008 | 5,45082 | -4,4508 | -0,0038 | 4,954064 | 0,0042 | 4,735 | |
| 4,742 | 5,66046 | -4,6605 | 5,699493 | 4,737 | ||||
| S1 | 5,2699 | S2 | 1,13615 | S3 | 0,3775 | |||
| F1 | 9,5399 | F2 | 12,1375 | F3 | -22,3 |
Т.к. F3<0, то М=1, N=2, передаточная функция имеет вид:
|
|
|
где b1=1; b2=-F3/F2=1,837; a1=1; a2=F1+b2=11,377; a3=F2+b2=13,975;
Тогда передаточная функция будет иметь вид:
|
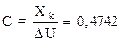
, где
Проверка адекватности:
σ = 
= 1,4032 %
На рисунке 5.5 изображен график передаточной функции по главному каналу регулирования.
Рисунок 5.5 – Кривая разгона
Исследование вспомогательного канала регулирования:
В результате эксперимента были получены следующие исходные данные:
Таблица 5.6 – Результаты эксперимента – вспомогательный канал регулирования
| Время - t | Выход - X | ΔX |
| 373,6 | 0,6 | |
| 375,08 | 2,08 | |
| 377,83 | 4,83 | |
| 378,05 | 5,05 | |
| 378,07 | 5,07 | |
| 378,09 | 5,07 |
Получение математической модели методом площадей
Таблица 5.7 – Результаты расчетов
| t | ΔX | Z | Q | 1-Q | Z(1-Q) | (1-2Q+Q^2/2) | Z(1-2Q+Q^2/2) | Xрасч |
| 0,6 | 0,881657 | 0,491041 | 0,508959 | 0,448727023 | 0,13848 | 0,12209 | 0,622 | |
| 2,08 | 0,589744 | 0,982082 | 0,017918 | 0,010566834 | -0,4819 | -0,2842 | 2,864 | |
| 4,83 | 0,047337 | 1,473123 | -0,47312 | -0,02239638 | -0,8612 | -0,0408 | 5,021 | |
| 0,013807 | 1,964165 | -0,96416 | -0,01331194 | -0,9994 | -0,0138 | 5,724 | ||
| 5,05 | 0,003945 | 2,455206 | -1,45521 | -0,00574046 | -0,8964 | -0,0035 | 5,319 | |
| 5,07 | 2,946247 | -1,94625 | -0,5523 | 4,828 | ||||
| S1 | 2,53649 | S2 | 1,4178451 | S3 | 0,7798 | |||
| F1 | 2,03649 | F2 | 1,8691816 | F3 | 1,1603 |
Т.к. X’(0)=0 и F3>0, то М=0, N=3, передаточная функция имеет вид:
|
|
|
 |  | ||
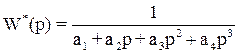где:
b1=1; a1=1; a2=F1=2,03649; a3=F2=1,869; a4=F3=1,1603
Тогда передаточная функция будет иметь вид:
|
, где
 |
Проверка адекватности:
σ =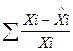 
= 8,64721 %
Рисунок 5.8 – Кривая разгона
Исследование вспомогательного канала возмущения:
Таблица 5.9 – Результаты эксперимента –канал возмущения
| Время - t | Выход - X | ΔX |
| 57,47 | ||
| 57,47 | -0,02 | |
| 57,45 | -0,737 | |
| 56,733 | -1,672 | |
| 55,798 | -2,19 | |
| 55,28 | -2,699 | |
| 54,771 | -3,031 | |
| 54,439 | -3,552 | |
| 53,918 | -4,0539 | |
| 53,4161 | -4,5558 | |
| 52,9142 | -5,0576 | |
| 52,4124 | -5,5595 | |
| 51,9105 | -6,0614 | |
| 51,4086 | -6,163 | |
| 51,307 | -6,172 | |
| 51,298 | -6,301 | |
| 51,169 | -6,372 | |
| 51,098 | -6,598 | |
| 50,872 | -6,772 | |
| 50,698 | -6,951 | |
| 50,519 | -7,158 | |
| 50,312 | -7,259 | |
| 50,211 | -7,332 | |
| 50,138 | -7,455 | |
| 50,015 | -7,568 | |
| 49,902 | -7,665 | |
| 49,805 | -7,68 | |
| 49,79 | -7,719 | |
| 49,751 | -7,738 | |
| 49,732 | -7,738 |
Получение математической модели методом площадей
Таблица 6 – Результаты расчетов
| t | ΔX | Z | Q | 1-Q | Z(1-Q) | (1-2Q+Q^2/2) | Z(1-2Q+Q^2/2) | Xрасч |
| -0,02 | 0,99742 | 0,11306 | 0,88694 | 0,884 | 0,7802688 | 0,77825 | 2,391 | |
| -0,737 | 0,90476 | 0,22612 | 0,77388 | 0,700 | 0,5733205 | 0,51872 | 3,225 | |
| -1,672 | 0,78392 | 0,33918 | 0,66082 | 0,518 | 0,3791551 | 0,29723 | 2,955 | |
| -2,19 | 0,71698 | 0,45225 | 0,54775 | 0,392 | 0,1977725 | 0,1418 | 2,337 | |
| -2,699 | 0,6512 | 0,56531 | 0,43469 | 0,283 | 0,0291727 | 0,019 | 1,878 | |
| -3,031 | 0,6083 | 0,67837 | 0,32163 | 0,195 | -0,1266441 | -0,077 | 1,721 | |
| -3,552 | 0,54096 | 0,79143 | 0,20857 | 0,112 | -0,2696782 | -0,1459 | 1,775 | |
| -4,0539 | 0,4761 | 0,90449 | 0,09551 | 0,045 | -0,3999293 | -0,1904 | 1,894 | |
| -4,5558 | 0,41125 | 1,01755 | -0,0176 | -0,007 | -0,5173976 | -0,2128 | 1,982 | |
| -5,0576 | 0,34639 | 1,13061 | -0,1306 | -0,045 | -0,6220831 | -0,2155 | 2,012 | |
| -5,5595 | 0,28153 | 1,24367 | -0,2437 | -0,068 | -0,7139857 | -0,201 | 2,001 | |
| -6,0614 | 0,21667 | 1,35674 | -0,3567 | -0,077 | -0,7931054 | -0,1718 | 1,978 | |
| -6,163 | 0,20354 | 1,4698 | -0,4698 | -0,095 | -0,8594423 | -0,1749 | 1,961 | |
| -6,172 | 0,20238 | 1,58286 | -0,5829 | -0,117 | -0,9129963 | -0,1848 | 1,956 | |
| -6,301 | 0,18571 | 1,69592 | -0,6959 | -0,129 | -0,9537675 | -0,1771 | 1,958 | |
| -6,372 | 0,17653 | 1,80898 | -0,809 | -0,142 | -0,9817558 | -0,1733 | 1,962 | |
| -6,598 | 0,14732 | 1,92204 | -0,922 | -0,135 | -0,9969613 | -0,1469 | 1,966 | |
| -6,772 | 0,12484 | 2,0351 | -1,0351 | -0,129 | -0,9993839 | -0,1248 | 1,967 | |
| -6,951 | 0,10171 | 2,14816 | -1,1482 | -0,116 | -0,9890236 | -0,1006 | 1,966 | |
| -7,158 | 0,07495 | 2,26123 | -1,2612 | -0,094 | -0,9658805 | -0,0724 | 1,965 | |
| -7,259 | 0,0619 | 2,37429 | -1,3743 | -0,085 | -0,9299545 | -0,0576 | 1,965 | |
| -7,332 | 0,05247 | 2,48735 | -1,4873 | -0,078 | -0,8812457 | -0,0462 | 1,965 | |
| -7,455 | 0,03657 | 2,60041 | -1,6004 | -0,058 | -0,819754 | -0,03 | 1,965 | |
| -7,568 | 0,02197 | 2,71347 | -1,7135 | -0,0376 | -0,7454795 | -0,0164 | 1,965 | |
| -7,665 | 0,00943 | 2,82653 | -1,8265 | -0,017 | -0,6584221 | -0,0062 | 1,965 | |
| -7,68 | 0,0075 | 2,93959 | -1,9396 | -0,014 | -0,5585818 | -0,0042 | 1,965 | |
| -7,719 | 0,00246 | 3,05266 | -2,0527 | -0,005 | -0,4459587 | -0,0011 | 1,965 | |
| -7,738 | 3,16572 | -2,1657 | -0,3205527 | 1,965 | ||||
| S1 | 9,34476 | S2 | 2,676146022 | S3 | 0,22413 | |||
| F1 | 35,379 | F2 | 307,9598156 | F3 | -1381,2 |
|
|
|
Проверка адекватности:
σ = 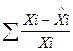= 82,92561 %
Рисунок 6.1 – Кривая разгона
Выводы
В результате проделанной работы и выполненных расчетов можно сказать, что метод площадей является одним удобных методов идентификации динамических характеристик объектов управления. Этот метод удобен как для реализации на ЭВМ, так и для ручного счета и обладает вполне удовлетворительной для практики точностью.
Метод предполагает идентификацию вне процесса управления, так как использует не результаты измерений при нормальной эксплуатации САУ, а требуется проведения специальных экспериментов по снятию кривой отклика объекта на ступенчатое возмущение на входе объекта. По этой экспериментально полученной кривой разгона определяется коэффициенты передаточной функции.
Расчеты показали, что в первых двух случаях модель адекватная, а в последнем случае при исследовании по вспомогательному каналу возмущения модель неадекватна.
Таким образом, получены передаточные функции объекта управления, которые буду использованы нами в следующем семестре при выполнении лабораторных работ по дисциплинам АТТП и АТС. Параметры этих передаточных функций приведены в таблице 5.8.
Таблица 5.8 – Полученные исходные данные для расчета настроек автоматических регуляторов в лабораторном практикуме по дисциплинам АТТП и АТС
| Ка-нал | Вход | Вы-ход | Передаточная функция | Метод определения параметров передаточной функции объекта | Найдены значения параметров передаточных функций |
| U | X | 
| Графический | С=0.62602 T=18 τ=2 | |
| U | X | 
| Метод площадей | С4=0.4742 a1=1 a2=11.377 a3=13.971 b1=1 b2=1.837 τ4=0 | |
| U | X1 | 
| Графический | С1=0.37809 T1=2.5 τ 1=0.5 | |
| V | X | 
| Графический | С2=0.49732 T2=74 τ 2=12 |
6 Список использованных источников.
1. Эйкхофф П. Основы идентификации систем управления. Пер. с англ. -М.: Мир, 1975, -683с.
2. Гроп Д. Методы идентификации систем. - M.: Мир, 1979.
3. Фомин Б.В., Яковлев В.Б. Моделирование производственных систем. - Киев: Вища школа. 1992.
4. Советов Б. Я., Яковлев С. А. Моделирование систем: Практикум — 3-е изд., перераб. и доп. — М.: Высш. шк., 2005. — 296 с: ил.
|
|
|
5. Советов Б. Я., Яковлев С. А. Моделирование систем: Учебник для вузов — 3-е юд., перераб. и доп. - М.: Высш. шк., 2001. - 343 с: ил.
6. Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е издание, перераб. и дополненное. -М.: Высшая школа, 1985. -327с.
7. Инков А.М. Моделирование и идентификация объектов управления. Методические указания к выполнению лабораторных работ для студентов специальности 050702. Шымкент, ЮКГУ, 2009 г., -52с.
8. Инков А.М. Моделирование и идентификация объектов управления. Методические указания к самостоятельным работам, СРСП и конспект лекций для студентов специальности 050702. Шымкент, Южно-Казахстанский Государственный Университет (ЮКГУ). 2008 г. - 102 стр., 4 таб., ил.
9. Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с.
10. Построение математических моделей химико-технологических процессов. Под ред. Дудникова Е.Г. - Л.: Химия, 1970. –312 с.
11. Райбман Н.С., Чадеев В.М. Построение моделей производства. - М.: Энергия, 1975.
12. Современные методы идентификации систем. Под ред. Эйкхоффа П. - М.: Мир, 1983.
13. Цыпкин Я.З. Основы информационной теории идентификации. - М.: Наука, 1986.
14. Райбман Н.С. Что такое идентификация. - М.: Наука, 1978
15. Харин Ю.С., Малюгин В.И., Кирлица В.П. - Основы имитационного и статистического моделирования. Минск,1997
16. Цирлин А.М., Балакирев В.С., Дудников Е.Г. Вариационные методы оптимизации управляемых объектов. М.: Наука, 1984.
17. Балакришнан А. Теория фильтрации Калмана: Пер. с англ. –М.:, Мир, 1988 -108с
18. Льюнг Л. Идентификация систем. Теория для пользователя. - M.: Наука, 1991
19. Рузинов Л.П. Статистические методы оптимизации химических процессов. -М.: Химия, 1972.
20. Рузинов Л.П., Слбодчикова Р.И. Планирование эксперимента в химии и химической технологии. -М.: Химия, 1980.
21. Бенькович Е.С. и др. Практическое моделирование динамических систем. -СПб: БХВ-Петербург, 2002.
22. Херхатер М., Партолль X. Mathcad 2000. Пер. с нем. - К.: Изд. ГруппаВНУ, Киев, 2000
23. Дьяконов В.П. Mathcad -14: учебный курс - СПб.: Питер, 2007
24. Боровиков В.П., Боровиков И.П. Statictica - статистический анализ и обработка данных в среде Windows,- M.: Инф. издат.дом «Филинъ», 2004
25. Фомин В Н., Фрадков О.Л., Якубович В.А. Адаптивное управление динамическими объектами. М: Наука, 1981.
26. Бокс Дж, Дженкинс. Анализ временных рядов. Прогноз и управление. Выпуск 1. –М.: Мир, 1970, 406с.
27. Бокс Дж, Дженкинс. Анализ временных рядов. Прогноз и управление. Выпуск 2. –М.: Мир, 1974, 193с.
28. Спиди Л., Браун Р, Гудвин Дж. Теория управления. Идентификация и оптимальное управление. –М.: Мир, 1973, 247с.
29. Сейдж Э.П., Уайт Ч. Оптимальное управление системами: Пер. с англ. /Под ред. Левина Б.Р.. –М.: Радио и связь, 1982. -398 с.
30. Смит Дж. Математическое и цифровое моделирование для инженеров и исследователей /Пер. с англ. –М.: Машиностроение, 1980. -271 с.
31. Автоматическое управление в химической промышленности: учебник для вузов. Под ред. Дудникова Е.Г. -М.: Химия, 1987. -368с.
32. Инков А.М. Автоматизация технических систем. Методические указания к самостоятельным работам и конспект лекций для студентов специальности 050702. Шымкент, Южно-Казахстанский Государственный Университет (ЮКГУ). 2008 г. - 82 стр., 4 таб., ил.
|
|
|
