 |
Метод Рунге–Кутта второго порядка точности
|
|
|
|
Вычисления по этому методу осуществляются в два этапа. На первом этапе по схеме Эйлера находится промежуточное значение 
 .
| (5.5) |
На втором этапе находится значение 
по схеме
 ,
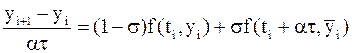| (5.6) |
где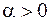 
, 
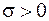– параметры. Подставляя из (5.5) в (5.6), имеем
 .
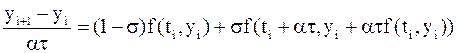| (5.7) |
Нетрудно проверить (разложение по формуле Тейлора), что схема (5.7) имеет второй порядок аппроксимации при условии 
. Частные случаи разностной схемы (5.7):
 .
| (5.8) |
Эта разностная схема носит название предиктор-корректор, или счет-пересчет. Первая схема из (5.8) – схема Эйлера с шагом 
(предиктор), вторая – схема со значением на полушаге (корректор).
Метод Рунге–Кутта четвертого порядка точности
Используется схема
 .
| (5.9) |
где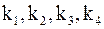 
– поправки, вычисляемые по формулам
 .
| (5.10) |
При определении по заданному 
необходимо четыре раза вычислять правую часть (5.9) в следующей последовательности: 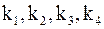. Если предположить достаточную гладкость 
(непрерывную дифференцируемость вплоть до производных 4-го порядка) и разложить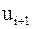 
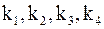, в окрестности 
, нетрудно показать, что невязка 
, т.е. разностная схема (5.9) имеет 4-й порядок аппроксимации.
Пример выполнения лабораторной работы №5
Требуется решить задачу Коши при помощи численных методов
.
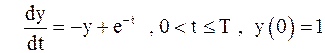Вводим функцию 
:
.
Задаем шаг, количество шагов по времени и начальное условие
.
Выводим длину расчетного временного интервала
.
Задаем точное значение решения (считается аналитически)
.
Метод Эйлера для решения задачи Коши
Вводим функцию, реализующую алгоритм метода Эйлера:
Вызываем данную функцию
.
Строим графики точного решения и приближенного, рассчитанного методом Эйлера:
Выводим значение погрешности
|
|
|
.
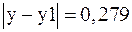Метод Рунге–Кутта второго порядка точности для решения задачи Коши
Вводим функцию, реализующую алгоритм метода Рунге–Кутта второго порядка точности:
Вызываем данную функцию
Строим графики точного решения и приближенного, рассчитанного методом Рунге–Кутта второго порядка точности:
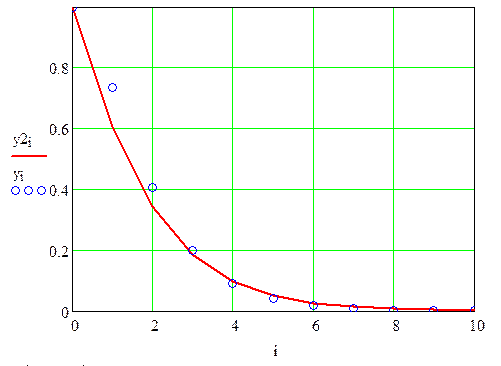
Выводим значение погрешности
.
Метод Рунге–Кутта четвертого порядка точности для решения задачи Коши
Вводим функцию, реализующую алгоритм метода Рунге-Кутта четвертого порядка точности
Вызываем данную функцию
.
Строим графики точного решения и приближенного, рассчитанного методом Рунге–Кутта четвертого порядка точности:
Выводим значение погрешности
.
Варианты заданий к лабораторной работе №5
Решить задачу Коши, используя методы Эйлера, Рунге–Кутта второго и четвертого порядков точности.
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
10. 
;
Содержание отчета
Отчет должен содержать:
1) титульный лист;
2) постановку задачи (согласно варианту);
3) точное решение задачи;
4) краткое описание методов решения задачи Коши;
5) программную реализацию данных методов;
6) выводы о проделанной работе.
Контрольные вопросы и задания
1. Какие численные методы решения задачи Коши вы знаете?
2. Запишите разностную схему решения задачи Коши на основе метода Эйлера.
3. Запишите разностную схему решения задачи Коши на основе метода Рунге–Кутта 2 порядка.
4. Приведите пример решения задачи Коши при помощи метода Эйлера.
5. Приведите пример решения задачи Коши при помощи метода Рунге–Кутта 2 порядка.
6. Какова погрешность метода Эйлера?
7. Определите погрешность решения задачи Коши методом Эйлера на конкретном примере.
8. Определите погрешность решения задачи Коши методом Рунге–Кутта 2 порядка на конкретном примере.
9. От чего зависит погрешность численного решения задачи Коши?
|
|
|
10*. Приведите пример решения системы дифференциальных уравнений.
|
|
|
