 |
Интерполяционный полином Ньютона
|
|
|
|
Задаем таблицу значений функции
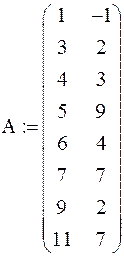 .
.
Вводим функцию расчета коэффициентов интерполяционного полинома Ньютона

Вызываем данную функцию
 .
.
Строим функцию интерполяционного полинома Ньютона
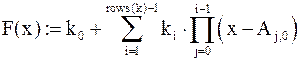 .
.
Выводим минимальное и максимальное значение аргумента


Вводим количество точек и шаг табуляции

 .
.
Устанавливаем счетчики
 .
.
Табулируем функцию
 .
.
Строим график функции интерполяционного полинома Ньютона
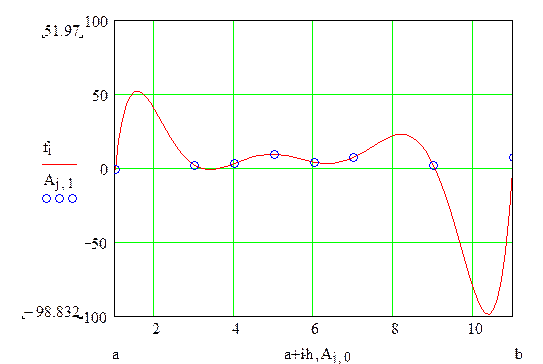
Интерполяционный кубический сплайн
Задаем таблицу значений функции
 .
.
Устанавливаем счетчики
 .
.
Считаем шаг
 .
.
Устанавливаем счетчики

 .
.
Задаем диагонали матрицы коэффициентов и столбец свободных членов согласно методу прогонки


 .
.
 .
.
Вводим функцию, реализующую алгоритм прогонки:

При помощи функции прогонки считаем значения коэффициентов 
 .
.
Переопределяем значения коэффициентов 



 .
.
Cчитаем значения коэффициентов  и
и 



 .
.
Вводим функцию интерполяционного кубического сплайна

Вводим количество точек
 .
.
Определяем минимальное и максимальное значение аргумента


Вводим шаг табуляции
 .
.
Табулируем функцию интерполяционного кубического сплайна

 .
.
Строим график функции

Метод наименьших квадратов
Задаем таблицу значений функции
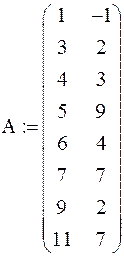
Устанавливаем счетчики
 .
.
Считаем значения 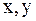
 .
.
Задаем СЛАУ согласно методу минимальных квадратов в случае линейной регрессии

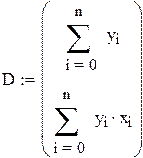
Решаем СЛАУ
 .
.
Строим линейную регрессионную функцию
 .
.
Устанавливаем счетчики
 .
.
Строим график линейной регрессионной функции

Считаем квадрат невязки
 .
.
Считаем квадрат невязки
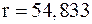 .
.
Задаем СЛАУ согласно методу минимальных квадратов в случае квадратичной регрессии
 ;
;  .
.
Решаем СЛАУ
|
|
|
 .
.
Строим квадратичную регрессионную функцию
 .
.
Строим график квадратичной регрессионной функции

Считаем квадрат невязки
 .
.
Считаем квадрат невязки
 .
.
Задаем СЛАУ согласно методу минимальных квадратов в случае кубической регрессии
 ;
;  .
.
Решаем СЛАУ
 .
.
Строим кубическую регрессионную функцию
 .
.
Строим график кубической регрессионной функции

Считаем квадрат невязки
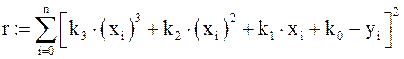 .
.
Считаем квадрат невязки
 .
.
Интерполяционный тригонометрический полином
Задаем таблицу значений функции
 .
.
Считаем число значений таблицы и задаем мнимую единицу

 .
.
Устанавливаем счетчики
 .
.
Считаем значение спектра


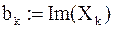 .
.
Вводим функцию интерполяционного тригонометрического полинома в случае четного числа узлов
 .
.
Устанавливаем счетчики
 .
.
Строим функцию интерполяционного тригонометрического полинома

Варианты заданий к лабораторной работе №6
По заданной таблице  значений функции найти
значений функции найти  как функцию от
как функцию от  на основе:
на основе:
а) интерполяционного полинома Лагранжа и Ньютона;
б) интерполяционного кубического сплайна;
в) метода минимальных квадратов для линейной, квадратичной и кубической регрессии.
| Вариант | Значения функции | |||||||||
| x | ||||||||||
| y | ||||||||||
| x | ||||||||||
| y | ||||||||||
| x | ||||||||||
| y | –3 | –5 |
| Вариант | Значения функции | |||||||||
| x | ||||||||||
| y | ||||||||||
| x | ||||||||||
| y | –2 | –6 | ||||||||
| x | ||||||||||
| y | –1 | –4 | ||||||||
| x | ||||||||||
| y | –1 | |||||||||
| x | ||||||||||
| y | ||||||||||
| x | ||||||||||
| y | –1 | |||||||||
| x | ||||||||||
| y | –1 |
|
|
|
г) интерполяционного тригонометрического полинома
| Вариант | y(0) | y(1) | y(2) | y(3) | y(4) | y(5) | y(6) | y(7) |
| –4 | – | |||||||
| –4 | –3 | |||||||
| – | ||||||||
| –4 | –5 | – | ||||||
| –4 | –4 | |||||||
| –5 | –2 | – | ||||||
| –5 | ||||||||
| – | ||||||||
Содержание отчета
Отчет должен содержать:
1) титульный лист;
2) постановку задачи (согласно варианту);
3) краткое описание методов решения задачи Коши;
4) программную реализацию данных методов;
5) выводы о проделанной работе.
Контрольные вопросы и задания
1. Какие виды приближения функции вы знаете?
2. Какие виды интерполяции функции вы знаете?
3. Приведите пример построения интерполяционного полинома при помощи метода Лагранжа.
4. Приведите пример построения интерполяционного полинома при помощи метода Ньютона.
5. Какой метод построения интерполяционного полинома является менее трудоемким: метод Лагранжа или метод Ньютона?
6. По заданной выборке найти оптимальную прямую методом наименьших квадратов.
7. По заданной выборке найти оптимальную параболу методом наименьших квадратов.
8. Приведите пример построения интерполяционного кубического сплайна.
9. Приведите пример построения интерполяционного тригонометрического полинома.
10. Как изменится трудоемкость дискретного преобразования Фурье в случае использования алгоритма быстрого преобразования Фурье?
Библиографический список
1. Калитки Н.Н. Численные методы. – М.: Наука, 1978.
2. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989.
3. Самарский А.А. Введение в численные методы. – М.: Наука, 1987.
4. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. – 2-е изд., испр. – М.: Физматлит, 2001. – 320 с. – ISBN 5-9221-0120-Х.
|
|
|
5. Стечкин С.Б., Субботин Ю.Н. Сплайны в вычислительной математике. – М.: Наука, 1976.
6. Чистяков А.Е., Алексеенко Е.В., Колгунова О.В. Вычислительные эксперименты с математическими моделями турбулентного обмена в мелководных водоемах // Известия ЮФУ. Технические науки. – 2008. №10 (87).– С 171-175.
7. Алексеенко Е.В., Сидоренко Б.В., Колгунова О.В., Чистяков А.Е. Сравнительный анализ классических и неклассических моделей гидродинамики водоемов с турбулентным обменом // Известия ЮФУ. Технические науки. – 2009. №8 (97). – С 6-18.
8. Лапин Д.В., Черчаго А.А., Чистяков А.Е. Совместные экспедиционные исследования гидрофизических параметров Азовского моря на многоцелевой яхте «Буревестник» и НИС т/х «Платов» // Известия ЮФУ. Технические науки. –2009, №8 (97). – С 82-89.
9. Чистяков А.Е. Трехмерная модель движения водной среды в Азовском море с учетом транспорта солей и тепла // Известия ЮФУ. Технические науки –2009. №8 (97). – С 75-82.
10. Чистяков А.Е. Теоретические оценки ускорения и эффективности параллельной реализации ПТМ скорейшего спуска// Известия ЮФУ. Технические науки. – 2010. №6(107). – С 237-249.
11. Чистяков А.Е. Об аппроксимации граничных условий трехмерной модели движения водной среды // Известия ЮФУ. Технические науки. – 2010. №6(107). – С 66-77.
12. Сухинов А.И., Чистяков А.Е., Алексеенко Е.В. Численная реализация трехмерной модели гидродинамики для мелководных водоемов на супервычислительной системе// Математическое моделирование. – 2011. – Т.23, №3, – С. 3-21.
13. Сухинов А.И., Чистяков А.Е., Бондаренко Ю.С. Оценка погрешности решения уравнения диффузии на основе схем с весами// Известия ЮФУ. Технические науки.– 2011. №8 (121). – С 6-13.
14. Сухинов А.И., Тимофеева Е.Ф. Чистяков А.Е. Построение и исследование дискретной математической модели расчета прибрежных волновых процессов// Известия ЮФУ. Технические науки. –2011. №8 (121). – С 22-32.
15. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Построение дискретной двумерной математической модели транспорта наносов// Известия ЮФУ. Технические науки. – 2011. №8 (121). – С 32-44.
16. Чистяков А.Е., Костырко Е.А. Математическое моделирование деформации стержня// Известия ЮФУ. Технические науки. –2011. №8(121). – С 57-61.
|
|
|
17. Сухинов А.И., Чистяков А.Е., Хачунц Д.С. Математическое моделирование движения многокомпонентной воздушной среды и транспорта загрязняющих веществ// Известия ЮФУ. Технические науки. –2011. №8(121). – С 73-79.
18. Сухинов А.И., Огурцов Е.С., Чистяков А.Е. Построение дискретной математической модели излучения электромагнитных волн линейной антенной решеткой из скошенных волноводов// Известия ЮФУ. Технические науки. –2011, №8(121). – С 129-139.
19. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Двумерная гидродинамическая модель, учитывающая динамическое перестроение геометрии дна мелководных водоемов// Известия ЮФУ. Технические науки. –2011. №8(121). – С 159-167.
20. Жорник А.И., Прокопенко Ю.А., Чистяков А.Е. Численное решение задачи индукционного нагрева полого цилиндра// Известия ЮФУ. Технические науки. –2011. №8(121). – С 175-182.
21. Сухинов А.И., Чистяков А.Е. Адаптивный модифицированный попеременно-треугольный итерационный метод для решения сеточных уравнений с несамосопряженным оператором// Математическое моделирование. – 2012. – Т.24, №1. – С. 3–20.
22. Дегтярева Е.Е., Чистяков А.Е. Моделирование транспорта наносов по данным экспериментальных исследований в Азовском море// Известия ЮФУ. Технические науки. –2012. №2 (127). – С 112-118.
23. Сухинов А.И., Чистяков А.Е. Параллельная реализация трехмерной модели гидродинамики мелководных водоемов на супервычислительной системе// Вычислительные методы и программирование: Новые вычислительные технологии. – 2012. – Т.13. – С. 290-297.
24. Сухинов А.И., Дегтярева Е.Е., Чистяков А.Е. Математическое моделирование транспорта донных отложений с учетом гидродинамических процессов// Известия ЮФУ. Технические науки. –2012. №6 (131). – С 57-62.
25. Никитина А.В., Чистяков А.Е., Фоменко Н.А. Применение адаптивного модифицированного попеременно–треугольного итерационного метода для численной реализации двумерной математической модели движения водной среды // Инженерный вестник Дона. – 2012. – Т.20, №2. – С. 335–339.
26. Сухинов А.И., Чистяков А.Е., Тимофеева Е.Ф., Шишеня А.В. Математическая модель расчета прибрежных волновых процессов// Математическое моделирование. – 2012. – Т.24, №8. – С. 32-44.
27. Сухинов А.И., Никитина А.В., Чистяков А.Е. Моделирование сценария биологической реабилитации Азовского моря // Математическое моделирование. – 2012. – Т.24, №9. – С. 3-21.
28. Дегтярева Е.Е., Проценко Е.А., Чистяков А.Е. Программная реализация трехмерной математической модели транспорта взвеси в мелководных акваториях// Инженерный вестник Дона. 2012. Т. 23. № 4-2. – С. 30.
29. Чистяков А.Е., Першина Ю.В. Решение задачи динамики популяций на основе модели хищник-жертва // Известия ЮФУ. Технические науки. 2013. № 1. С. 142-149.
|
|
|
30. Сухинов А.И., Никитина А.В., Чистяков А.Е., Семенов И.С. Математическое моделирование условий формирования заморов в мелководных водоемах на многопроцессорной вычислительной системе// Вычислительные методы и программирование: Новые вычислительные технологии. – 2013. – Т.14. – С. 113–122.
31. Чистяков А.Е., Хачунц Д.С. Программная реализация двумерной задачи движения воздушной среды// Известия ЮФУ. Технические науки. –2013. №4. – С 15-21.
32. Чистяков А.Е., Семенякина А.А. Применение методов интерполяции для восстановления донной поверхности// Известия ЮФУ. Технические науки. –2013. №4. – С 21-28.
33. Чистяков А.Е., Кузнецова И.Ю. Задача расчета и прогнозирования процесса подъема уровня воды в мелководных водоемах// Известия ЮФУ. Технические науки. –2013. №4. – С 28-36.
34. Сухинов А.И., Чистяков А.Е., Фоменко Н.А. Методика построения разностных схем для задачи диффузии-конвекции-реакции, учитывающих степень заполненности контрольных ячеек// Известия ЮФУ. Технические науки. –2013. №4. – С 87-96.
35. Сухинов А.И., Чистяков А.Е., Чекина М.Д. Описание математической модели процесса перемещения сыпучих веществ с использованием уравнения Сен-Венана // Известия ЮФУ. Технические науки. – 2013. №4. – С 96-104.
36. Сухинов А.И., Чистяков А.Е., Шишеня А.В. Модификация метода минимальных поправок для решения сеточных уравнений с несамосопряженным оператором // Известия ЮФУ. Технические науки. –2013. №4. – С. 194-202.
37. Сухинов А. И., Чистяков А. Е., Шишеня А. В. Оценка погрешности решения уравнения диффузии на основе схем с весами// Матем. моделирование, 25:11 (2013). – С. 53-64.
38. Сухинов А. И., Чистяков А. Е., Проценко Е. А. Математическое моделирование транспорта наносов в прибрежной зоне мелководных водоемов// Матем. моделирование, 25:12 (2013). – С. 65-82.
39. Сухинов А.И., Чистяков А.Е., Проценко Е.А. Математическое моделирование транспорта наносов в прибрежных водных системах на многопроцессорной вычислительной системе Вычислительные методы и программирование: новые вычислительные технологии. – 2014. – Т. 15, № 4. – С. 610-620.
40. Buzalo, N., Ermachenko, P., Bock, T., Bulgakov, A., Chistyakov, A., Sukhinov, A., Zhmenya, E., Zakharchenko, N. Mathematical modeling of microalgae-mineralization-human structure within the environment regeneration system for the biosphere compatible city. Procedia Engineering. Volume 85, Issue C. – 2014. – P. 84-93.
41. Проценко Е.А., Чистяков А.Е., Шретер С.А., Сухинов А.А. Сравнение трудоемкостей численной реализации явной и неявной схем для задачи транспорта наносов в прибрежных водных системах // Известия ЮФУ. Технические науки. – 2014, № 12 (161). – С. 210-219.
42. Лапин Д.В., Чистяков А.Е., Сухинов А.А. Численное решение прямых и обратных задач диффузии-конвекции на многопроцессорных системах для прогноза и ретроспективного анализа водных экосистем // Известия ЮФУ. Технические науки. – 2014, № 12 (161). – С. 230-242.
43. Чистяков А.Е., Фоменко Н.А., Проценко Е.А., Тимофеева Е.Ф., Григорян Л.А. Результаты численного моделирования деформации плоской волн// Фундаментальные исследования. – 2015, № 2-3. – С. 476-480.
44. Сухинов А.И., Хачунц Д.С., Чистяков А.Е. Параллельные алгоритмы для прогноза состояния воздушной среды рекреационных зон прибрежных систем// Вестник компьютерных и информационных технологий. – 2015, № 5 (131). – С. 55-60.
45. Сухинов А.И., Хачунц Д.С., Чистяков А.Е. Математическая модель распространения примеси в приземном слое атмосферы и ее программная реализация на многопроцессорной вычислительной системе// Вестник Уфимского государственного авиационного технического университета. – 2015. – Т. 19, № 1. – С. 213-223.
46. Сухинов А.И., Чистяков А.Е., Семенякина А.А., Никитина А.В. Параллельная реализация задач транспорта веществ и восстановления донной поверхности на основе схем повышенного порядка точности // Вычислительные методы и программирование. – 2015. – Т. 16, № 2. – С. 256-267.
47. Сухинов А.И., Угольницкий Г.А., Усов А.Б., Никитина А.В., Пучкин М.В., Семенов И.С., Чистяков А.Е. Дифференциально-игровая модель предотвращения заморов в мелководных водоемах // Управление большими системами. Выпуск 55. – 2015. – С.343-361.
48. Бузало Н.С., Ермаченко П.А., Никитина А.В., Проценко Е.А., Чистяков А.Е. Трехмерная математическая модель динамики жидкости и концентрации воздушных пузырьков в карусельном аэpотенке // Современные проблемы науки и образования. – 2015. – № 1; URL: http://www.science-education.ru/121-19511 (дата обращения: 04.06.2015).
49. Чистяков А.Е., Хачунц Д.С., Никитина А.В., Проценко Е.А., Кузнецова И.Ю. Библиотека параллельных итерационных методов решателей СЛАУ для задачи конвекции-диффузии на основе декомпозиции по одному пространственному направлению // Современные проблемы науки и образования. – 2015. – № 1; URL: http://www.science-education.ru/121-19510 (дата обращения: 04.06.2015).
50. Сухинов А.И., Проценко Е.А., Чистяков А.Е., Шретер С.А. Сравнение вычислительных эффективностей явной и неявной схем для задачи транспорта наносов в прибрежных водных системах// Вычислительные методы и программирование. – 2015. – Т 16, №3. – С. 328-338.
51. Сухинов А.И., Хачунц Д.С., Чистяков А.Е. Математическая модель распространения примеси в приземном слое атмосферы прибрежной зоны и ее программная реализация// Журнал вычислительной математики и математической физики, 2015, том 55, № 7. – С. 118–134.
52. Никитина А.В., Семенякина А.А., Чистяков А.Е., Проценко Е.А., Яковенко И.В. Применение схем повышенного порядка точности для решения задач биологической кинетики на многопроцессорной вычислительной системе // Фундаментальные исследования. – 2015, № 12-3. – С. 500-504.
53. Чистяков А.Е., Хачунц Д.С., Тимофеева Е.Ф., Фоменко Н.А. Программная реализация дискретной математической модели расчета прибрежных волновых процессов на основе регуляризованных по Б.Н. Четверушкину явных схем на вычислительных системах с массовым параллелизмом // Фундаментальные исследования. – 2015, № 12-3. – С. 540-544.
54. Кажаров Х.А., Ляпунова И.А., Чистяков А.Е. Программная реализация численного решения обратной задачи транспорта веществ // Инженерный вестник Дона. – 2015. – Т. 38, № 4 (38). – С. 50.
55. Сухинов А.И., Чистяков А.Е., Семенякина А.А., Никитина А.В. Численное моделирование экологического состояния Азовского моря с применением схем повышенного порядка точности на многопроцессорной вычислительной системе // Компьютерные исследования и моделирование. – 2016. – Т. 8, № 1. – С. 151-168.
56. Сухинов А.И., Чистяков А.Е., Якобовский М.В. Точность численного решения уравнения диффузии-конвекции на основе разностных схем второго и четвертого порядков погрешности аппроксимации // Вестник Южно-Уральского государственного университета. Серия: Вычислительная математика и информатика. – 2016. – Т. 5, № 1. – С. 47-62.
57. Хачунц Д.С., Чистяков А.Е. Моделирование процессов переноса загрязняющих веществ в приземном слое атмосферы прибрежной зоны // монография. – Таганрог: Изд-во ЮФУ, 2015. – 169 с.
58. Чистяков А.Е. Математическое моделирование гидродинамических процессов, транспорта взвесей и наносов в прибрежных системах // диссертация на соискание ученой степени доктора физико-математических наук / Южный федеральный университет. Таганрог, 2015.
|
|
|


