 |
Метод симметричных составляющих
|
|
|
|
Для расчета несимметричных режимов трехфазных электрических цепей применяется метод симметричных составляющих, основанный на представлении любой трехфазной несимметричной системы электрических или магнитных величин (токов, напряжений, магнитных потоков) в виде суммы (наложения) трех симметричных режимов. Эти симметричные режимы образуют в совокупности исходную несимметричную систему величин и носят название симметричных составляющих прямой, обратной и нулевой последовательностей.
Несимметричный режим, таким образом, оказывается представленным в виде трех симметричных режимов (составляющих исходного режима), одновременно существующих в одной и той же трехфазной цепи.
Рис. 4.5
На рис. 4.5 для примера представлены симметричные составляющие несимметричной системы напряжений.
Система прямой последовательности образует симметричную трехлучевую звезду U 1A, U 1B, U 1C с порядком следования максимумов напряжения фаз А → В → С → А. Фазным величинам прямой последовательности присваивается индекс 1. Мгновенные значения напряжений прямой последовательности могут быть получены при вращении звезды напряжений по направлению стрелки с частотой ω0 в виде проекций соответствующих векторов на вертикальную ось.
Система обратной последовательности образует симметричную трехлучевую звезду U 2A, U 2B, U 2C с порядком следования фаз А → С → В → А, то есть противоположным порядку следования фаз прямой последовательности.
Система нулевой последовательности состоит из трех равных векторов U 0A = U 0B = U 0C.
Векторами, показанными на рис. 4.5, могут изображаться как комплексные амплитуды, так и комплексные действующие значения напряжений последовательностей.
|
|
|
Мгновенные значения симметричных составляющих всех фаз могут быть получены в виде проекций векторов, вращающихся с угловой скоростью ω 0 в положительном направлении (против часовой стрелки). При этом направления вращения всех трех систем векторов одно и то же. Проекции можно рассматривать на любую из координатных осей (+1, +j).
Взаимное расположение и величина векторов прямой, обратной и нулевой последовательностей зависят от вида и степени несимметрии.
Для расчетов бывает достаточным знание векторов фазы А: U 1A, U 2A, U 0, векторы других фаз определяются через них.
Разложение на симметричные составляющие
Если известны (заданы) фазные величины несимметричной системы, например напряжения U A, U B, U C, то симметричные составляющие находятся по формулам (для фазы А, причем часто индекс,,А'' опускается):
(4.3)
где 
комплексный оператор поворота вектора в положительном направлении на угол 
, тогда а 2 – соответствует повороту на угол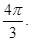 
Если определены векторы фазных величин различных последовательностей, рис. 4.5, то векторы этих величин в фазах В и С могут быть выражены через значения величины особой фазы А:
U 1A = U 1; U 1B = a2 U 1; U 1C = a U1;
U 2A = U 2; U 2B = a U 2 ;U 2C = a2 U 2; (4.4)
U 0A = U 0B = U 0C = U 0.
В данном случае напряжения в фазах А, В, С, то есть по существу исходная несимметричная система напряжений, определяется как сумма соответствующих симметричных составляющих:
UA = U1A + U2A + U0 = U1 + U2 + U0;
U B = U 1B + U 2B + U 0 = a2 U 1 + a U 2 + U 0; (4.5)
U C = U 1C + U 2C + U 0 = a U 1 + a2 U 2 + U 0.
Расчет несимметричного режима при симметрии
Трехфазной цепи
Предположим, что несимметричный режим трехфазной цепи, представленной на рис. 4.3, заключается в несимметрии ЭДС Е А, Е В, Е С, создаваемых генератором.
|
|
|
Разложим несимметричную систему ЭДС на симметричные составляющие. Далее изобразим схемы замещения для токов различных последовательностей, рис. 4.6.
Рис. 4.6
ЭДС Е 1, Е 2 и Е 0 находятся по формулам вида (4.3). Сопротивления элементов для различных последовательностей могут отличаться, в зависимости от вида последовательности, поэтому им присваивается индекс 1,2 или 0.
Проведя расчет токов I 1, I 2, I 0 по соответствующим схемам замещения, найдем действительные значения токов фаз генераторной ветви I ГА, I ГВ, I Г0, воспользовавшись формулами вида (4.5).
Следует заметить, что токи нулевой последовательности, схема рис. 4.6,в, могут возникать только в случае, если точки нейтралей 0 – 0` - 0``соединены нейтральным проводом. Если нейтральный провод обладает ненулевым сопротивлением Z 0, то оно учитывается в сопротивлении Z10. При отсутствии цепи нейтрали 0 – 0` - 0`` контур для протекания тока I 0 оказывается разомкнутым.
|
|
|
