 |
Расчет несимметричного режима при несимметрии
|
|
|
|
Трехфазной цепи
Несимметрия в трехфазной цепи может возникнуть из–за несимметрии нагрузки или вследствие несимметричного короткого замыкания.
Предположим, что несимметрия образовалась в точке,, а '' цепи, (рис. 4.7), вследствие возникшего неравенства по фазам сопротивлений нагрузки Z НГ . На схеме генератор Г с ЭДС ЕГ и внутренним сопротивлением Х Г передает мощность в приемную систему С через линию с сопротивлением Z 1 + Z 2. Приемная система представлена эквивалентным источником ЭДС, равным напряжению UC. Системы ЭДС ЕГ и U C – симметричны, также симметричны и цепи линии связи Z 1 и Z 2. Однако, из-за несимметрии нагрузки Z НГ в трехфазной цепи возникает несимметричный режим. При этом векторы напряжений U A, U B, U C в точке,, а '', и токи I A, I B, I C образуют несимметричные системы напряжений и токов.
Для расчета несимметричного режима используется метод симметричных составляющих.
Неизвестные величины U A, U B, U C, образующие несимметричную систему напряжений, запишем через их симметричные составляющие U 1, U 2, U 0.

Рис. 4.7
Воспользуемся далее заменой напряжений на несимметричных сопротивлениях нагрузки Z нг эквивалентными ЭДС. Такая замена возможна, если учесть приведенную для пояснения схему, рис. 4.8.
Используя такую замену, несимметричный режим трехфазной цепи можно представить схемой, показанной на рис. 4.9. На этой схеме между точками а, в, с фаз линии и нейтралью (точка 0) вместо напряжений U A, U B, U C включены симметричные составляющие их эквивалентных ЭДС: U 1А, U 2А, U 0А (для фазы А).
|

|
|
|
|
Верхний ряд симметричных ЭДС в точках а, в, с представляет собой прямую последовательность, второй – обратную, нижний – нулевую.

Рис. 4.9
Используя принцип наложения, расчет токов последовательностей ведется раздельно. Отдельно для каждой последовательности составляется схема замещения. На рис. 4.10 представлены схемы замещения последовательностей (для фазы А).
На схеме замещения прямой последовательности (рис. 4.10,а) Е и U – соответственно ЭДС генератора и ЭДС приемной системы. Это источники ЭДС прямой последовательности, то есть той последовательности, с которой совпадает симметричная составляющая эквивалентной ЭДС U 1A, включенная в ветви нагрузки вместо падения напряжения на сопротивлении нагрузки.
На схемах замещения обратной, рис. 4.10,б, и нулевой, рис. 4.10,в, последовательностей в ветвях генератора и системы отсутствуют источники ЭДС соответствующей последовательности, и только в ветви нагрузки оказываются включенными соответствующие ЭДС: U 2A и U 0A.

Рис. 4.10
Уравнения второго закона Кирхгофа, записанные для каждой последовательности, имеют вид:
 (4.7)
(4.7)
где Z 1 Σ, Z 2 Σ, Z 0 Σ – сопротивления схем замещения соответствующих последовательностей относительно точки несимметрии а – 0 (сопротивления между точками а – 0 равны нулю); Е Σ – эквивалентная (суммарная ЭДС) прямой последовательности относительно точек а – 0.
В уравнениях (4.7) шесть неизвестных: U 1А, U 2А, U 0А, I 1А, I 2А, I 0А. Недостающие три уравнения для определения этих величин получают из граничных условий, которыми характеризуется тот или иной вид несимметрии в точке ее возникновения. В данном случае несимметрия определяется неравенствами сопротивлений нагрузки Z AH Г 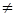 Z BH Г
Z BH Г 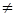 Z CH Г. Тогда для фазных напряжений U A, U B, U C по закону Ома можно записать:
Z CH Г. Тогда для фазных напряжений U A, U B, U C по закону Ома можно записать:
|
|
|
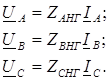 (4.8)
(4.8)
Уравнения (4.8) и представляют собой недостающие три уравнения для системы шести уравнений с шестью неизвестными. Причем, в уравнениях (4.8) необходимо фазные напряжения U A, U B, U C и токи I A, I B, I C представить через их симметричные составляющие U 1А, U 2А, U 0А и I 1А, I 2А, I 0А.
Решение системы уравнений (4.7) и (4.8) дает значения этих симметричных составляющих, а следовательно и истинные значения этих параметров по фазам могут быть рассчитаны по формулам вида (4.5).
,,Распределение'' симметричных составляющих, найденных в точке несимметрии (главным образом токов) по ветвям схемы производят обычным порядком с использованием теории линейных цепей.
Значения токов в каждом линейном проводе находят по их симметричным составляющим с использованием формул вида (4.5).
Заметим, что при глухих несимметричных коротких замыканиях и при обрывах линейных проводов граничные условия (4.8) существенно упрощаются, что позволяет находить значения симметричных составляющих и фазных параметров по готовым аналитическим формулам.
|
|
|



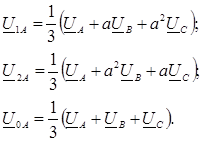 (4.6)
(4.6)